双向冒泡排序算法(非常详细,动图演示)
双向冒泡排序又叫鸡尾酒排序、搅拌排序等,是冒泡排序算法的改进版本,排序效率更高。
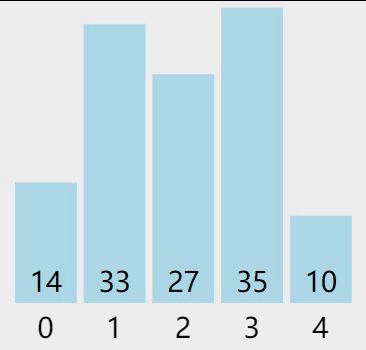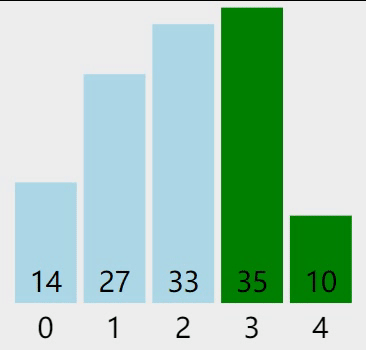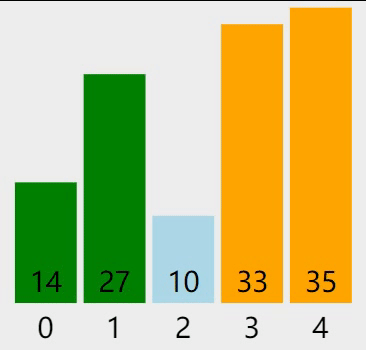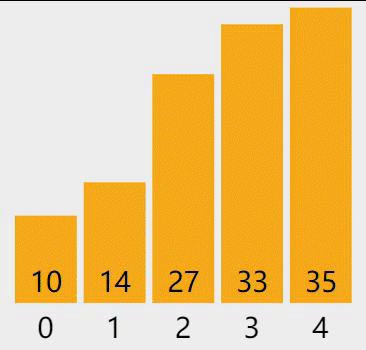
图 1 普通的冒泡排序
从待排序序列的第一个元素开始,比较相邻元素的大小,找到最大(或最小)的元素并移动到序列的末尾。重复整个过程,最终就可以得到一个有序的序列。
双向冒泡排序算法对图 1 的排序过程进行了优化,接下来仍以 {14, 33, 27, 35, 10} 进行升序排序为例,带大家了解双向冒泡排序。
1) 最初的待排序序列是 {14, 33, 27, 35, 10},和普通的冒泡排序一样,从第一个元素 14 向后查找,通过相邻元素的比较,找到最大的元素并移动到序列的末尾,过程如下图所示:
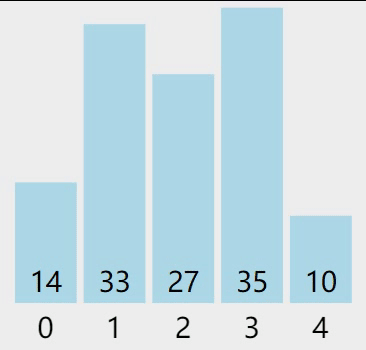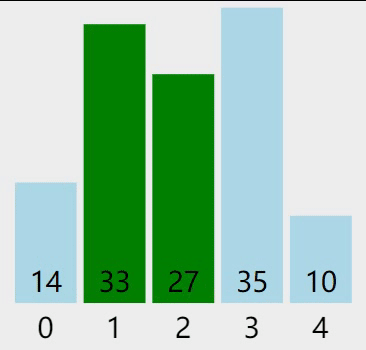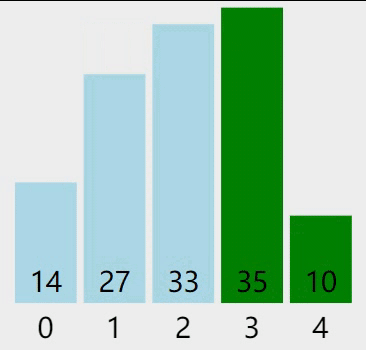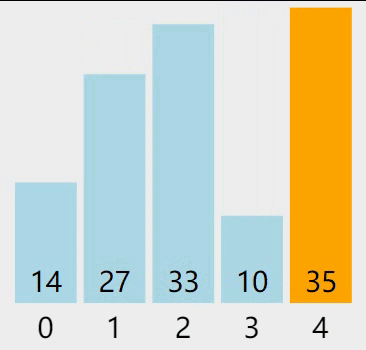
图 2 第一轮从前向后冒泡
在图 2 的基础上,待排序序列变成了 {14, 27, 33, 10}。接下来从末尾元素 10 开始向前查找,通过相邻元素的比较,找到最小的元素并移动到序列的开头。

图 3 第一轮从后往前冒泡
经过了第 1 步,从元素 14 向后查找,找到了最大值 35;再从元素 10 向前查找,找到了最小值 10。最终,待排序序列变成了 {14, 27, 33}。
2) 采用和第 1 步相同的方法,从 {14, 27, 33} 中的第一个元素 14 开始向后查找,通过相邻元素的对比,最终可以找到最大值 33 并移动到序列的末尾,待排序序列变成了 {14, 27}。

图 4 第二轮从前往后冒泡
继续从 {14, 27} 中最后一个元素 27 开始向前查找,可以找到最小值 14 并移动到序列的开头,待排序序列变成了 {27}。

图 5 第二轮从后往前冒泡
3) 由于待排序序列 {27} 只有 1 个元素,不再需要冒泡排序,此时整个序列 {10, 14, 27, 33, 35} 就是一个升序序列。
普通的冒泡排序算法,每轮排序只能找出一个最值;而双向冒泡排序算法,每轮排序可以找出一个最大值和一个最小值。如下是双向冒泡排序实现升序排序的伪代码:
下面是使用双向冒泡排序对 {14, 33, 27, 35, 10} 完成升序排序的 Java 程序:
下面是使用双向冒泡排序对 {14, 33, 27, 35, 10} 完成升序排序的 Python 程序:
传统的冒泡排序只会从一个方向(通常是从头到尾)比较元素,每次只能找到一个最值(最大值或者最小值);而双向冒泡排序算法先从头到尾比较一次,紧接着再反向比较一次,每次能找最大值和最小值。
和传统和冒泡排序算法相比,在某些场景中,双向冒泡排序算法可以减少比较和交换的次数,特别是对于部分有序的待排序序列,排序效率提升的非常明显。
注意,尽管双向冒泡排序在某些情况下比传统的冒泡排序更高效,但它的实现思路并没有颠覆性地创新,它的时间复杂度仍然和传统的冒泡排序算法相同,还是
阅读本文之前,读者要先搞清楚普通的冒泡排序算法,不了解的请猛击《冒泡排序算法》一文系统学习。
双向冒泡排序
先回忆一下普通的冒泡排序算法,比如对 {14, 33, 27, 35, 10} 进行升序排序,过程如下图所示:
图 1 普通的冒泡排序
从待排序序列的第一个元素开始,比较相邻元素的大小,找到最大(或最小)的元素并移动到序列的末尾。重复整个过程,最终就可以得到一个有序的序列。
双向冒泡排序算法对图 1 的排序过程进行了优化,接下来仍以 {14, 33, 27, 35, 10} 进行升序排序为例,带大家了解双向冒泡排序。
1) 最初的待排序序列是 {14, 33, 27, 35, 10},和普通的冒泡排序一样,从第一个元素 14 向后查找,通过相邻元素的比较,找到最大的元素并移动到序列的末尾,过程如下图所示:

图 2 第一轮从前向后冒泡
在图 2 的基础上,待排序序列变成了 {14, 27, 33, 10}。接下来从末尾元素 10 开始向前查找,通过相邻元素的比较,找到最小的元素并移动到序列的开头。

图 3 第一轮从后往前冒泡
经过了第 1 步,从元素 14 向后查找,找到了最大值 35;再从元素 10 向前查找,找到了最小值 10。最终,待排序序列变成了 {14, 27, 33}。
2) 采用和第 1 步相同的方法,从 {14, 27, 33} 中的第一个元素 14 开始向后查找,通过相邻元素的对比,最终可以找到最大值 33 并移动到序列的末尾,待排序序列变成了 {14, 27}。

图 4 第二轮从前往后冒泡
继续从 {14, 27} 中最后一个元素 27 开始向前查找,可以找到最小值 14 并移动到序列的开头,待排序序列变成了 {27}。

图 5 第二轮从后往前冒泡
普通的冒泡排序算法,每轮排序只能找出一个最值;而双向冒泡排序算法,每轮排序可以找出一个最大值和一个最小值。如下是双向冒泡排序实现升序排序的伪代码:
BidBubbleSort(list): // list 表示待排序序列
low <- 1
high <- length(list) // [low, high] 表示待排序序列
while low < high: // 当 low 不小于 high 时,表明排序完成
for i <- low to high: // 从第 low 个元素向后查找,找到最大值并移动到序列的末尾
if(list[i] > list[i+1]):
swap(list[i] , list[i+1])
high <- high - 1 // 找到最大值之后,待排序序列变成了 [low, hight-1]
for i <- high to low: // 从第 high 个元素向前查找,找到最小值并移动到序列的开头
if(list[i] < list[i-1]):
swap(list[i] , list[i-1])
low <- low + 1 // 找到最小值之后,待排序序列变成了 [low+1, hight]
双向冒泡排序的具体实现
下面是使用双向冒泡排序对 {14, 33, 27, 35, 10} 完成升序排序的C语言程序:
#include<stdio.h>
#define N 5 // 定义一个宏,表示数组的长度为5
// 定义一个函数BidBubbleSort,接收一个长度为N的整型数组作为参数
void BidBubbleSort(int list[N]) {
int i, temp; // 定义用于循环的变量i和用于交换元素值的temp
int low = 0;
int high = N - 1; // 指定 list 数组中 [low,high] 区域内的元素为待排序序列
// 当 low 不小于 high 时,表明排序完成
while (low < high) {
// 从第 low 个元素向后查找,找到最大值并移动到序列的末尾
for (i = low; i < high; i++) {
if (list[i] > list[i + 1]) {
temp = list[i];
list[i] = list[i + 1];
list[i + 1] = temp;
}
}
// 找到最大值之后,待排序序列变成了 [low, hight-1]
high--;
// 从第 high 个元素向前查找,找到最小值并移动到序列的开头
for (i = high; i > low; i--) {
if (list[i] < list[i - 1]) {
temp = list[i];
list[i] = list[i - 1];
list[i - 1] = temp;
}
}
// 找到最小值之后,待排序序列变成了 [low+1, hight]
low++;
}
}
// 主函数开始
int main() {
int i = 0; // 定义用于循环的变量i,初始化为0
int list[N] = { 14,33,27,35,10 }; // 定义并初始化一个长度为N的数组list
BidBubbleSort(list); // 对数组list进行冒泡排序
// 输出已排好序的序列
for (i = 0; i < N; i++) {
printf("%d ", list[i]);
}
return 0;
}
下面是使用双向冒泡排序对 {14, 33, 27, 35, 10} 完成升序排序的 Java 程序:
public class {
// 定义一个函数BidBubbleSort,接收一个长度为N的整型数组作为参数
public static void BidBubbleSort(int[] list) {
int i, temp; // 定义用于循环的变量i和用于交换元素值的temp
int low = 0;
int high = list.length - 1; // 指定list数组中 [low,high] 区域内的元素为待排序序列
// 当 low 不小于 high 时,表明排序完成
while (low < high) {
// 从第 low 个元素向后查找,找到最大值并移动到序列的末尾
for (i = low; i < high; i++) {
if (list[i] > list[i + 1]) {
temp = list[i];
list[i] = list[i + 1];
list[i + 1] = temp;
}
}
// 找到最大值之后,待排序序列变成了 [low, hight-1]
high--;
// 从第 high 个元素向前查找,找到最小值并移动到序列的开头
for (i = high; i > low; i--) {
if (list[i] < list[i - 1]) {
temp = list[i];
list[i] = list[i - 1];
list[i - 1] = temp;
}
}
// 找到最小值之后,待排序序列变成了 [low+1, hight]
low++;
}
}
public static void main(String[] args) {
int[] list = {14, 33, 27, 35, 10}; // 定义并初始化一个长度为N的数组list
BidBubbleSort(list); // 对数组list进行冒泡排序
// 输出已排好序的序列
for (int i = 0; i < list.length; i++) {
System.out.print(list[i] + " ");
}
}
}
下面是使用双向冒泡排序对 {14, 33, 27, 35, 10} 完成升序排序的 Python 程序:
def BidBubbleSort(list):
i, temp = 0, 0 # 定义用于循环的变量i和用于交换元素值的temp
low, high = 0, len(list) - 1 # 指定list数组中[low, high]区域内的元素为待排序序列
while low < high:
# 从第low个元素向后查找,找到最大值并移动到序列的末尾
for i in range(low, high):
if list[i] > list[i + 1]:
temp, list[i], list[i + 1] = list[i], list[i + 1], list[i] # 交换元素值
# 找到最大值之后,待排序序列变成了[low, hight-1]
high -= 1
# 从第high个元素向前查找,找到最小值并移动到序列的开头
for i in range(high, low, -1):
if list[i] < list[i - 1]:
temp, list[i], list[i - 1] = list[i], list[i - 1], list[i] # 交换元素值
# 找到最小值之后,待排序序列变成了[low+1, hight]
low += 1
# 主函数开始
if __name__ == '__main__':
list = [14, 33, 27, 35, 10] # 定义并初始化一个列表list
BidBubbleSort(list) # 对列表list进行冒泡排序
# 输出已排好序的序列
for i in range(len(list)):
print(list[i], end=' ')
运行程序,结果为:
10 14 27 33 35
总结
双向冒泡排序算法是传统冒泡排序算法的改进版本,它对排序过程进行了优化,排序效率更高。传统的冒泡排序只会从一个方向(通常是从头到尾)比较元素,每次只能找到一个最值(最大值或者最小值);而双向冒泡排序算法先从头到尾比较一次,紧接着再反向比较一次,每次能找最大值和最小值。
和传统和冒泡排序算法相比,在某些场景中,双向冒泡排序算法可以减少比较和交换的次数,特别是对于部分有序的待排序序列,排序效率提升的非常明显。
注意,尽管双向冒泡排序在某些情况下比传统的冒泡排序更高效,但它的实现思路并没有颠覆性地创新,它的时间复杂度仍然和传统的冒泡排序算法相同,还是
O(n2)。 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: