多数元素问题(非常详细,图文并茂)
多数元素问题指的是在包含 n 个元素的 nums 数组中,找到出现次数大于 ⌊ n/2 ⌋ 的元素。
例如,nums 数组是 {3, 2, 3},它包含 3 个元素,其中出现次数大于 1( ⌊ 3/2 ⌋ )次的元素是 3。
再例如, nums 数组是 {2, 2, 1, 1, 1, 2, 2},它包含 7 个元素,其中出现次数大于 3( ⌊ 7/2 ⌋ )次的元素是 2。
多数元素问题的解决思路有很多种,本节带领大家用分治算法解决这个问题。
1) 首先,将整个数组不断地进行拆分,直至各个数组无法再分(只剩下一个元素)为止。拆分过程如下图所示:
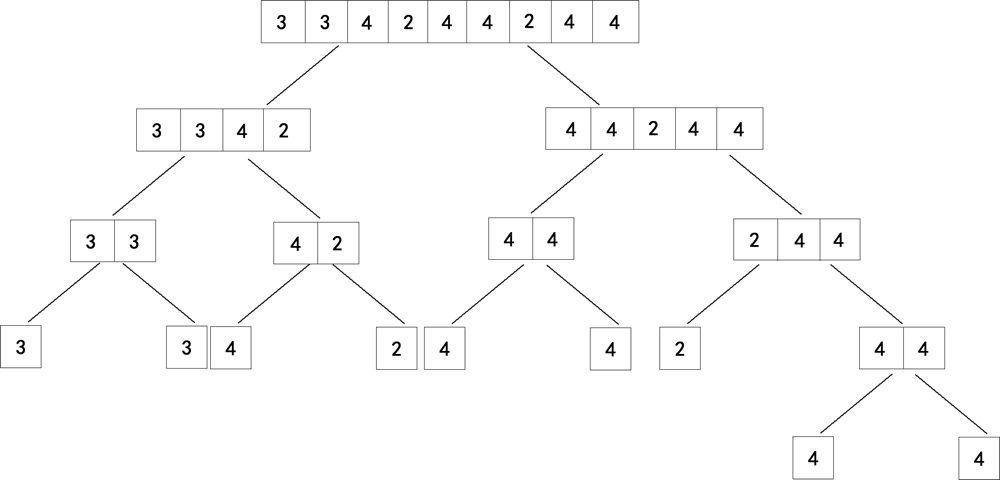
图1:拆分整个数组
最终,{3, 3, 4, 2, 4, 4, 2, 4, 4} 被拆分成了 9 个子数组,每个数组里只包含 1 个元素,它就是当前数组中出现次数大于 0( ⌊ 1/2 ⌋ )次的元素。
2) 经过第 1 步的拆分,每个子数组很轻易能找到出现次数最多的元素。在此基础上,每次合并两个子数组,直至将所有的子数组整合成完整的数组。对于要合并的两个子数组,已经得知了它们各自出现次数最多的元素,假设为 a 和 b:
所有子数组合并的过程如下图所示:
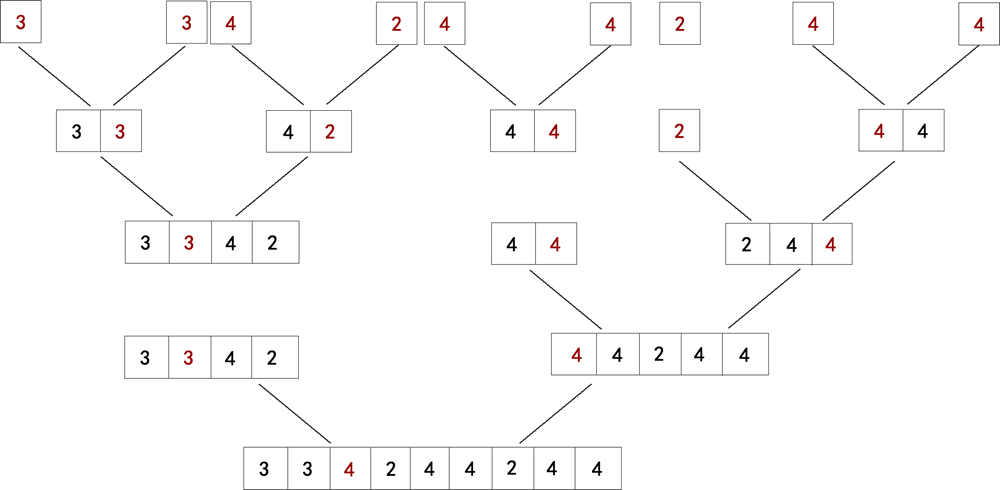
图2:合并所有的子数组
下面的伪代码描述了分治算法解决多数元素问题的过程:
下面是用分治算法实现多数元素问题的 Java 程序:
下面是用分治算法实现多数元素问题的 Python 程序:
运行程序,输出结果为:
例如,nums 数组是 {3, 2, 3},它包含 3 个元素,其中出现次数大于 1( ⌊ 3/2 ⌋ )次的元素是 3。
再例如, nums 数组是 {2, 2, 1, 1, 1, 2, 2},它包含 7 个元素,其中出现次数大于 3( ⌊ 7/2 ⌋ )次的元素是 2。
多数元素问题的解决思路有很多种,本节带领大家用分治算法解决这个问题。
分治算法解决多数元素问题
接下来以 {3, 3, 4, 2, 4, 4, 2, 4, 4} 数组为例,梳理分治算法解决多数元素问题的整个思路。1) 首先,将整个数组不断地进行拆分,直至各个数组无法再分(只剩下一个元素)为止。拆分过程如下图所示:

图1:拆分整个数组
最终,{3, 3, 4, 2, 4, 4, 2, 4, 4} 被拆分成了 9 个子数组,每个数组里只包含 1 个元素,它就是当前数组中出现次数大于 0( ⌊ 1/2 ⌋ )次的元素。
2) 经过第 1 步的拆分,每个子数组很轻易能找到出现次数最多的元素。在此基础上,每次合并两个子数组,直至将所有的子数组整合成完整的数组。对于要合并的两个子数组,已经得知了它们各自出现次数最多的元素,假设为 a 和 b:
- 如果 a 和 b 相等,那么在合并后的数组中,出现次数最多的也一定是 a(或者 b);
- 如果 a 和 b 不等,就需要在合并后的数组中分别统计 a 和 b 出现的次数,进而得知出现次数最多的元素。
所有子数组合并的过程如下图所示:

图2:合并所有的子数组
飘红的元素为各个数组中出现次数最多的元素。
结合图 1 和图 2 不难看出,合并各个数组的过程,其实是拆分数组的逆过程。最终,整个数组中出现次数最多的元素是 4。下面的伪代码描述了分治算法解决多数元素问题的过程:
findMajorElement(nums, low, high):
if low == high:
return nums[low]
// 递归方式拆分数组
mid = (high - low) / 2 + low
left = findMajorElement(nums, low, mid)
right = findMajorElement(nums, mid + 1, high)
//确定当前数组中出现次数最多的元素
if left == right:
return left
// 统计 left 元素在当前数组中出现的次数
leftCount = findMajorElementCount(nums, left, low, high)
// 统计 right 元素在当前数组中出现的次数
rightCount = findMajorElementCount(nums, right, low, high)
// 确定当前数组中出现次数最多的元素
if leftCount > rightCount:
return left
else:
return right
分治算法实现多数元素问题
下面是用分治算法实现多数元素问题的 C 语言程序:
#include <stdio.h>
// 统计 target 元素在 nums 数组中出现的次数
int findMajorElementCount(int nums[], int target, int low, int high) {
int count = 0;
for (int i = low; i <= high; i++) {
if (target == nums[i]) {
++count;
}
}
return count;
}
int majorityElement(int nums[], int low, int high) {
// 递归出口,当前数组拆分区域中只剩一个元素时,递归才结束
if (low == high) {
return nums[low];
}
// 递归方式拆分数组
int mid = (high - low) / 2 + low;
int left = majorityElement(nums, low, mid);
int right = majorityElement(nums, mid + 1, high);
// 确定当前数组中出现次数最多的元素
if (left == right) {
return left;
}
// 统计 left 元素在当前数组中出现的次数
int leftCount = findMajorElementCount(nums, left, low, high);
// 统计 right 元素在当前数组中出现的次数
int rightCount = findMajorElementCount(nums, right, low, high);
// 确定当前数组中出现次数最多的元素
return (leftCount > rightCount) ? left : right;
}
int main() {
int nums[] = { 3, 3, 4, 2, 2, 2, 2, 4, 4 };
int numsSize = sizeof(nums) / sizeof(nums[0]);
// 调用解决多数元素问题的函数
int result = majorityElement(nums, 0, numsSize - 1);
printf("出现次数最多的元素是: %d\n", result);
return 0;
}
下面是用分治算法实现多数元素问题的 Java 程序:
public class MajorityElement {
// 统计 target 元素在 nums 数组中出现的次数
static int findMajorElementCount(int[] nums, int target, int low, int high) {
int count = 0;
for (int i = low; i <= high; i++) {
if (target == nums[i]) {
++count;
}
}
return count;
}
static int majorityElement(int[] nums, int low, int high) {
// 递归出口,当前数组拆分区域中只剩一个元素时,递归才结束
if (low == high) {
return nums[low];
}
// 递归方式拆分数组
int mid = (high - low) / 2 + low;
int left = majorityElement(nums, low, mid);
int right = majorityElement(nums, mid + 1, high);
// 确定当前数组中出现次数最多的元素
if (left == right) {
return left;
}
// 统计 left 元素在当前数组中出现的次数
int leftCount = findMajorElementCount(nums, left, low, high);
// 统计 right 元素在当前数组中出现的次数
int rightCount = findMajorElementCount(nums, right, low, high);
// 确定当前数组中出现次数最多的元素
return (leftCount > rightCount) ? left : right;
}
public static void main(String[] args) {
int[] nums = {3, 3, 4, 2, 2, 2, 2, 4, 4};
int numsSize = nums.length;
// 调用解决多数元素问题的函数
int result = majorityElement(nums, 0, numsSize - 1);
System.out.println("出现次数最多的元素是: " + result);
}
}
下面是用分治算法实现多数元素问题的 Python 程序:
def find_major_element_count(nums, target, low, high):
count = 0
for i in range(low, high + 1):
if target == nums[i]:
count += 1
return count
def majority_element(nums, low, high):
# 递归出口,当前数组拆分区域中只剩一个元素时,递归才结束
if low == high:
return nums[low]
# 递归方式拆分数组
mid = (high - low) // 2 + low
left = majority_element(nums, low, mid)
right = majority_element(nums, mid + 1, high)
# 确定当前数组中出现次数最多的元素
if left == right:
return left
# 统计 left 元素在当前数组中出现的次数
left_count = find_major_element_count(nums, left, low, high)
# 统计 right 元素在当前数组中出现的次数
right_count = find_major_element_count(nums, right, low, high)
# 确定当前数组中出现次数最多的元素
return left if left_count > right_count else right
if __name__ == "__main__":
nums = [3, 3, 4, 2, 2, 2, 2, 4, 4]
nums_size = len(nums)
# 调用解决多数元素问题的函数
result = majority_element(nums, 0, nums_size - 1)
print("出现次数最多的元素是:", result)
运行程序,输出结果为:
出现次数最多的元素是: 2
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: