寻找图中是否存在路径（非常详细，图文并茂）

我们在《并查集》一节详细介绍了并查集这种存储结构，本节趁热打铁，带领读者用并查集解决一个实际问题，即判断图中指定的两个顶点之间是否存在有效的路径。

举个简单的例子，观察下图：

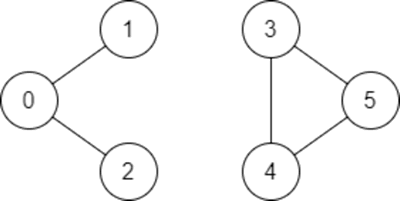
图 1 包含 6 个顶点的图

这是一张包含 6 个顶点的图，其中顶点 1 和顶点 2 是连通的，它们之间存在的有效路径是1-0-2；而顶点 1 和顶点 5 之间是不连通的，它们之间不存在有效的路径。

并查集判断图中是否存在路径

判断图中指定的两个顶点之间是否存在有效路径，用并查集解决此问题的思路是：将整张图存储到并查集中，图中相互连接的各个顶点同处一个集合，它们的根结点是相同的。也就是说，对于图中指定的两个顶点，如果他们的根结点相同，就表明它们是连通的，它们之间就一定存在有效的路径；反之如果它们的根结点不同，表明它们处于不同的集合，它们不是连通的，它们之间就不存在有效的路径。

仍以图 1 为例，把整张图（n = 6, edges = [ [0,1], [0,2], [3,5], [5,4], [4,3] ]）存储到并查集中，最终并查集的存储状态如下图所示：

图 2 存储图的并查集

可以看到，下标 0 、1 和 2 位置上存储的根结点都是 0，表明顶点 0、1 和 2 同处一个集合，它们之间是相互连通的；同理，下标 3、4 和 5 位置上存储的根结点都是 3，表明顶点 3、4 和 5 同处一个集合，它们之间是相互连通的。

判断图中两个顶点之间是否存在有效的路径，只需要分别找到两个顶点的根结点，如果它们的根结点相同，表明它们同处一个集合，它们之间就至少存在一条有效的路径；反之如果根结点不同，表明它们身处不同的集合，它们之间不存在有效的路径。

并查集解决图中是否存在路径

下面是用并查集解决“图中是否存在路径”的C语言程序：

#include <stdio.h>
#include <stdlib.h>

typedef enum { false, true } bool;
#define MAX_SIZE 1000  // 可以根据需要调整最大尺寸

// 并查集数组
typedef struct {
    int parent[MAX_SIZE];
    int count;
}UnionFind;

// 初始化并查集
void initialize(UnionFind* uf, int size) {
    for (int i = 0; i < size; i++) {
        uf->parent[i] = i;
    }
    uf->count = size;
}

// 查找根节点（代表元素）
int find(UnionFind* uf, int x) {
    if (uf->parent[x] != x) {
        uf->parent[x] = find(uf, uf->parent[x]); // 路径压缩
    }
    return uf->parent[x];
}

// 合并两个元素所在的集合
void unionSets(UnionFind* uf, int x, int y) {
    //找到两个元素所在集合的代表元素
    int xRoot = find(uf, x);
    int yRoot = find(uf, y);
    //如果代表元素不同，表明它们是两个集合，将它们合并
    if (xRoot != yRoot) {
        uf->parent[xRoot] = yRoot; // uf->parent[yRoot] = xRoot;
        uf->count--;
    }
}

//判断图中是否存在路径，n 表示图中顶点的数量，edgs数组存储的是图中所有的边，len 表示边的数量，source 和 destination 表示要进行判断的两个顶点
bool validPath(int n, int(*edgs)[2], int len, int source, int destination) {
    UnionFind uf;
    initialize(&uf, n);
    // 把图存储到并查集中
    for (int  i = 0; i < len; i++)
    {
        unionSets(&uf, edgs[i][0], edgs[i][1]);
    }
    //判断 source 和 destination 是否同处一个集合
    if (find(&uf, source) == find(&uf, destination)) {
        return true;
    }
    else
    {
        return false;
    }
}

// 主函数
int main() {  
    int edgs[5][2] = { {0,1},{0,2},{3,5},{5,4},{4,3} };

    //判断顶点 1 和 2 之间是否存在有效的路径
    bool ret = validPath(6, edgs, 5, 1, 2);
    if (ret == true) {
        printf("顶点 1 和顶点 2 之间存在有效的路径\n");
    }
    else
    {
        printf("顶点 1 和顶点 2 不存在有效的路径\n");
    }

    //判断顶点 1 和 5 之间是否存在有效的路径
    ret = validPath(6, edgs, 5, 1, 5);
    if (ret == true) {
        printf("顶点 1 和顶点 5 之间存在有效的路径\n");
    }
    else
    {
        printf("顶点 1 和顶点 5 不存在有效的路径\n");
    }

    return 0;
}

下面是用并查集解决“图中是否存在路径”的 Java 程序：

// 并查集类，用于处理集合合并和查找操作
public class UnionFind {
    private int[] parent;  // 记录节点的父节点
    private int count;     // 记录集合的数量

    // 构造函数，初始化并查集，每个节点的父节点初始为自己，集合数量为节点个数
    public UnionFind(int size) {
        parent = new int[size];
        for (int i = 0; i < size; i++) {
            parent[i] = i;
        }
        count = size;
    }

    // 查找根节点（代表元素）的方法，同时进行路径压缩
    public int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);  // 路径压缩
        }
        return parent[x];
    }

    // 合并两个元素所在的集合
    public void unionSets(int x, int y) {
        int xRoot = find(x);
        int yRoot = find(y);
        if (xRoot != yRoot) {
            parent[xRoot] = yRoot;  // 合并集合
            count--;
        }
    }

    // 获取当前集合的数量
    public int getCount() {
        return count;
    }
}

// 主程序类，用于测试并查集是否存在有效路径
public class ValidPath {
    // 判断图中是否存在路径的方法
    public static boolean validPath(int n, int[][] edges, int len, int source, int destination) {
        UnionFind uf = new UnionFind(n);
        // 将图存储到并查集中
        for (int i = 0; i < len; i++) {
            uf.unionSets(edges[i][0], edges[i][1]);
        }
        // 判断 source 和 destination 是否属于同一个集合
        return uf.find(source) == uf.find(destination);
    }

    // 主函数，用于测试并查集是否能够判断有效路径
    public static void main(String[] args) {
        int[][] edges = {{0, 1}, {0, 2}, {3, 5}, {5, 4}, {4, 3}};

        // 判断顶点 1 和 2 之间是否存在有效的路径
        boolean ret = validPath(6, edges, 5, 1, 2);
        if (ret) {
            System.out.println("顶点 1 和顶点 2 之间存在有效的路径");
        } else {
            System.out.println("顶点 1 和顶点 2 不存在有效的路径");
        }

        // 判断顶点 1 和 5 之间是否存在有效的路径
        ret = validPath(6, edges, 5, 1, 5);
        if (ret) {
            System.out.println("顶点 1 和顶点 5 之间存在有效的路径");
        } else {
            System.out.println("顶点 1 和顶点 5 不存在有效的路径");
        }
    }
}

下面是用并查集解决“图中是否存在路径”的 Python 程序：

class UnionFind:
    def __init__(self, size):
        # 初始化并查集，每个节点的父节点初始为自己，集合数量为节点个数
        self.parent = [i for i in range(size)]
        self.count = size

    def find(self, x):
        # 查找根节点（代表元素）的方法，同时进行路径压缩
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])  # 路径压缩
        return self.parent[x]

    def union_sets(self, x, y):
        # 合并两个元素所在的集合
        x_root = self.find(x)
        y_root = self.find(y)
        if x_root != y_root:
            self.parent[x_root] = y_root  # 合并集合
            self.count -= 1

    def get_count(self):
        # 获取当前集合的数量
        return self.count

def valid_path(n, edges, source, destination):
    uf = UnionFind(n)
    # 将图存储到并查集中
    for edge in edges:
        uf.union_sets(edge[0], edge[1])
    # 判断 source 和 destination 是否属于同一个集合
    return uf.find(source) == uf.find(destination)

if __name__ == "__main__":
    edges = [[0, 1], [0, 2], [3, 5], [5, 4], [4, 3]]

    # 判断顶点 1 和 2 之间是否存在有效的路径
    ret = valid_path(6, edges, 1, 2)
    if ret:
        print("顶点 1 和顶点 2 之间存在有效的路径")
    else:
        print("顶点 1 和顶点 2 不存在有效的路径")

    # 判断顶点 1 和 5 之间是否存在有效的路径
    ret = valid_path(6, edges, 1, 5)
    if ret:
        print("顶点 1 和顶点 5 之间存在有效的路径")
    else:
        print("顶点 1 和顶点 5 不存在有效的路径")

运行程序，输出结果为：

顶点 1 和顶点 2 之间存在有效的路径
顶点 1 和顶点 5 不存在有效的路径

寻找图中是否存在路径（非常详细，图文并茂）

并查集判断图中是否存在路径

并查集解决图中是否存在路径

相关文章