C++双向链表的基本操作（图文并茂，附带实例）

在单链表中，每个节点都被附加了一个指针域，指向下一个节点。在单链表中只能向后操作，不能向前操作。

为了向前、向后操作方便，可以给每个节点都附加两个指针域，一个指针域存储上一个节点的地址，另一个指针域存储下一个节点的地址。这种链表被称为“双向链表”，如下图所示：


从上图可以看出，双向链表的每个节点都包含三个域：数据域和两个指针域。两个指针域分别存储上一个和下一个节点的地址，即指向前驱和后继。

双向链表的节点结构体定义如下图所示：

双向链表插入节点

单链表只有一个指针域，是向后操作的，不能向前操作，因此若要在单链表的节点 i 之前插入一个元素，则必须先找到节点 i-1。在节点 i 之前插入一个元素相当于把新节点放在节点 i-1 之后。

而双向链表因为有两个指针，可以向前、后两个方向操作，所以可以直接找到节点 i，把新节点插入节点 i 之前。

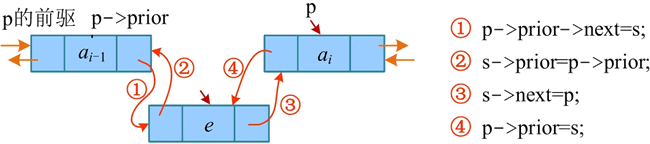
注意，这里假设节点 i 是存在的，若节点 i 不存在，而节点 i-1 存在，则还需要找到节点 i-1，将新节点揑入节点 i-1 之后，如下图所示：


其中：

• ① 表示将 s 的地址赋值给 p 的前驱的 next 指针域，即 p 的前驱的 next 指针指向 s；
• ② 表示将 p 的前驱的地址赋值给 s 的 prior 指针域，即 s 的 prior 指针指向 p 的前驱；
• ③ 表示将 p 的地址赋值给 s 的 next 指针域，即 s 的 next 指针指向 p；
• ④ 表示将 s 的地址赋值给 p 的 prior 指针域，即 p 的 prior 指针指向 s。

因为 p 的前驱无标记，一旦修改了 p 的 prior 指针，p 的前驱就找不到了，所以最后修改这个指针。修改指针顺序的原则：先修改没有指针标记的那一端。

算法代码：

bool ListInsert_L(DuLinkList &L, int i, int e) { // 在第 i 个位置之前插入元素 e
    DuLinkList p = L, s;
    int j = 0;
    while (p && j < i) { // 查找节点 i，p 指向该节点
        p = p->next;
        j++;
    }
    if (!p || j > i) // i > n+1 或者 i < 1
        return false;
    s = new DuLNode;   // 生成新节点
    s->data = e;       // 将新节点的数据域置为元素 e
    p->prior->next = s;
    s->prior = p->prior;
    s->next = p;
    p->prior = s;
    return true;
}

双向链表删除节点

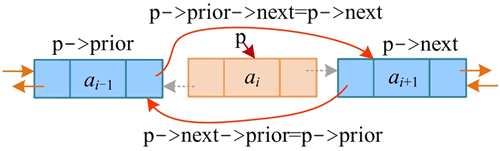
删除一个节点，实际上就是跳过这个节点。在单链表中必须先找到节点 i-1，才能把节点 i 跳过去。在双向链表中则不必如此，直接找到节点 i，之后修改指针即可，如下图所示：

• “p->prior->next=p->next”表示将 p 的后继的地址赋值给 p 的前驱的 next 指针域。即 p 的前驱的 next 指针指向 p 的后继。注意，等号右侧是节点的地址，等号左侧是节点的指针域。
• “p->next->prior=p->prior”表示将 p 的前驱的地址赋值给 p 的后继的 prior 指针域。即 p 的后继的 prior 指针指向 p 的前驱。此项修改的前提是 p 的后继存在，若不存在，则无须修改此项。

这样就跳过了节点 p。之后用 delete p 释放被删除节点占用的内存空间。在删除节点时，修改指针没有顺序，先修改哪个指针都可以。

算法代码：

bool ListDelete_L(DuLinkList &L, int i) { // 删除第 i 个元素
    DuLinkList p = L;
    int j = 0;
    while (p && j < i) { // 查找节点 i，p 指向该节点
        p = p->next;
        j++;
    }
    if (!p || j > i) // 当 i > n 或 i < 1 时，删除位置不合理
        return false;
    if (p->next) // 若 p 的后继存在
        p->next->prior = p->prior;
    p->prior->next = p->next;
    delete p;    // 释放被删除节点占用的内存空间
    return true;
}