聚类分析是什么,K-Means算法实现聚类分析(附带实例)
聚类分析是一种探索性的分析,在分类的过程中,人们不必事先给出一个分类的标准,聚类分析能够从样本数据出发,自动进行分类。
聚类分析是根据事物本身的特性研究个体的一种方法,目的在于将相似的事物归类。它的原则是同一类中的个体有较大的相似性,不同类别之间的个体差异性很大。
聚类算法的特征如下:
1) 适用于没有先验知识的分类。如果没有这些事先的经验或一些国际标准、国内标准、行业标准,分类便会显得随意和主观。这时只要设定比较完善的分类变量,就可以通过聚类分析法得到较为科学合理的类别。
2) 可以处理多个变量决定的分类。例如,根据消费者购买量的大小进行分类比较容易,但如果在进行数据挖掘时,要求根据消费者的购买量、家庭收入、家庭支出、年龄等多个指标进行分类,通常比较复杂,而聚类分析法可以解决这类问题。
3) 是一种探索性分析方法,能够分析事物的内在特点和规律,并根据相似性原则对事物进行分组,是数据挖掘中常用的一种技术。
聚类分析被应用于很多方面:
数据预处理还包括将孤立点移出数据,孤立点是不依附于一般数据行为或模型的数据,因此孤立点经常会导致有偏差的聚类结果,为了得到正确的聚类,我们必须将它们剔除。
例如,通常通过定义在特征空间的距离度量来评估不同对象的相异性,很多距离度量都应用在一些不同的领域,一个简单的距离度量,如欧氏距离,经常被用作反映不同数据间的相异性。
常用来衡量数据点间的相似度的距离有海明距离、欧氏距离、马氏距离等,公式如下:
① 海明距离:
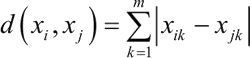
② 欧氏距离:
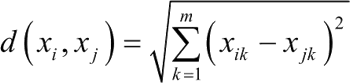
③ 马氏距离:
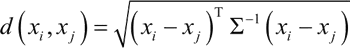
划分方法一般从初始划分和最优化一个聚类标准开始,主要方法包括:
Crisp Clustering 和 Fuzzy Clustering 是划分方法的两个主要技术,划分方法聚类是基于某个标准产生一个嵌套的划分系列,它可以度量不同类之间的相似性或一个类的可分离性,用来合并和分裂类。其他的聚类方法还包括基于密度的聚类、基于模型的聚类、基于网格的聚类。
K-Means 聚类算法是比较常用的聚类算法,容易理解和实现相应功能的代码。K-Means 聚类如下图所示:
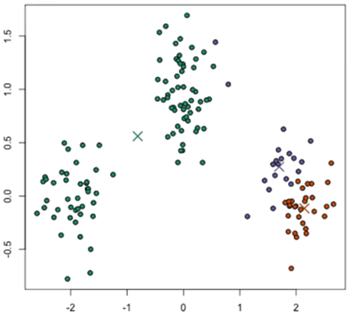
图 4 K-Means聚类
首先,我们要确定聚类的数量,并随机初始化它们各自的中心点,如图 4 中的“×”,然后通过算法实现最优。
K-Means 算法的逻辑如下:
K-Means 的优点是模型执行速度较快,因为我们真正要做的是计算点和类别的中心之间的距离,因此,它的线性复杂性是 O(n)。另一方面,K-Means 有两个缺点:一个是先确定聚类的簇数量;另一个是随机选择初始聚类中心点坐标。
本例中使用了kmeans_pytorch包中的K-Means算法实现聚类分析,因此首先需要安装该第三方包。
操作步骤如下:
1) 导入相关第三方库,代码如下:
2) 设置运行环境,代码如下:
3) 读取数据源,代码如下:
4) 设置聚类模型,代码如下:
5) 绘制聚类后的散点图,代码如下:
本实验通过花瓣长度、花瓣宽度、花萼长度、花萼宽度4个特征对植物花卉进行了分类。运行建模步骤中的代码,模型的聚类结果如下:
聚类分析的聚类中心点如下:
带聚类中心点的聚类散点图如下图所示:
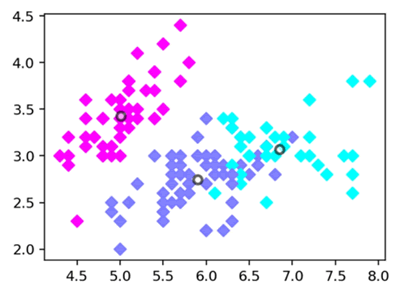
图 5 聚类效果图
聚类分析是根据事物本身的特性研究个体的一种方法,目的在于将相似的事物归类。它的原则是同一类中的个体有较大的相似性,不同类别之间的个体差异性很大。
聚类算法的特征如下:
1) 适用于没有先验知识的分类。如果没有这些事先的经验或一些国际标准、国内标准、行业标准,分类便会显得随意和主观。这时只要设定比较完善的分类变量,就可以通过聚类分析法得到较为科学合理的类别。
2) 可以处理多个变量决定的分类。例如,根据消费者购买量的大小进行分类比较容易,但如果在进行数据挖掘时,要求根据消费者的购买量、家庭收入、家庭支出、年龄等多个指标进行分类,通常比较复杂,而聚类分析法可以解决这类问题。
3) 是一种探索性分析方法,能够分析事物的内在特点和规律,并根据相似性原则对事物进行分组,是数据挖掘中常用的一种技术。
聚类分析被应用于很多方面:
- 在商业上,聚类分析被用来发现不同的客户群,并且通过购买模式刻画不同的客户群特征;
- 在西北,聚类分析被用来对动植物进行分类和对基因进行分类,以获取对种群固有结构的认识;
- 在保险行业,聚类分析通过一个高的平均消费来鉴定汽车保险单持有者的分组,同时根据住宅类型、价值、地理位置来鉴定一个城市的房产分组;
- 在互联网应用上,聚类分析被用来在网上进行文档归类来修复信息。
聚类分析建模
一般情况下,聚类分析的建模步骤如下:1) 数据预处理
数据预处理包括选择数量、类型和特征的标度,它依靠特征选择和特征抽取:- 特征选择是选择重要的特征;
- 特征抽取是把输入的特征转换为一个新的显著特征,它们经常被用来获取一个合适的特征集来为避免“维数灾”进行聚类。
数据预处理还包括将孤立点移出数据,孤立点是不依附于一般数据行为或模型的数据,因此孤立点经常会导致有偏差的聚类结果,为了得到正确的聚类,我们必须将它们剔除。
2) 为衡量数据点间的相似度定义一个距离函数
既然相似性是定义一个类的基础,那么不同数据之间在同一个特征空间相似度的衡量对于聚类步骤是很重要的,由于特征类型和特征标度的多样性,距离度量必须谨慎,它经常依赖于应用。例如,通常通过定义在特征空间的距离度量来评估不同对象的相异性,很多距离度量都应用在一些不同的领域,一个简单的距离度量,如欧氏距离,经常被用作反映不同数据间的相异性。
常用来衡量数据点间的相似度的距离有海明距离、欧氏距离、马氏距离等,公式如下:
① 海明距离:
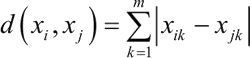
② 欧氏距离:
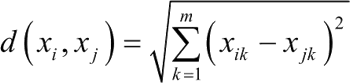
③ 马氏距离:
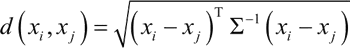
3)聚类或分组
将数据对象分到不同的类中是一个很重要的步骤,数据基于不同的方法被分到不同的类中。划分方法和层次方法是聚类分析的两个主要方法。划分方法一般从初始划分和最优化一个聚类标准开始,主要方法包括:
- Crisp Clustering,它的每个数据都属于单独的类。
- Fuzzy Clustering,它的每个数据都可能在任何一个类中。
Crisp Clustering 和 Fuzzy Clustering 是划分方法的两个主要技术,划分方法聚类是基于某个标准产生一个嵌套的划分系列,它可以度量不同类之间的相似性或一个类的可分离性,用来合并和分裂类。其他的聚类方法还包括基于密度的聚类、基于模型的聚类、基于网格的聚类。
4) 评估输出
评估聚类结果的质量是另一个重要的阶段,聚类是一个无管理的程序,也没有客观的标准来评价聚类结果,它是通过一个类的有效索引来评价的。一般来说,几何性质,包括类之间的分离和类自身内部的耦合一般都用来评价聚类结果的质量。K-Means 聚类算法是比较常用的聚类算法,容易理解和实现相应功能的代码。K-Means 聚类如下图所示:

图 4 K-Means聚类
首先,我们要确定聚类的数量,并随机初始化它们各自的中心点,如图 4 中的“×”,然后通过算法实现最优。
K-Means 算法的逻辑如下:
- 通过计算当前点与每个类别的中心之间的距离,对每个数据点进行分类,然后归到与之距离最近的类别中。
- 基于迭代后的结果,计算每一类内全部点的坐标平均值(即质心),作为新类别的中心。
- 迭代重复以上步骤,直到类别的中心点坐标在迭代前后变化不大。
K-Means 的优点是模型执行速度较快,因为我们真正要做的是计算点和类别的中心之间的距离,因此,它的线性复杂性是 O(n)。另一方面,K-Means 有两个缺点:一个是先确定聚类的簇数量;另一个是随机选择初始聚类中心点坐标。
植物花卉特征聚类
本例根据花瓣长度、花瓣宽度、花萼长度、花萼宽度4个特征进行聚类分析。数据集内包含 3 类共 150 条记录,每类各 50 个数据。本例中使用了kmeans_pytorch包中的K-Means算法实现聚类分析,因此首先需要安装该第三方包。
操作步骤如下:
1) 导入相关第三方库,代码如下:
#导入相关库 import torch import numpy as np import pandas as pd import matplotlib.pyplot as plt from kmeans_pytorch import kmeans from torch.autograd import Variable import torch.nn.functional as F
2) 设置运行环境,代码如下:
if torch.cuda.is_available(): # 判断是否有可用的 CUDA 设备
device = torch.device('cuda:0') # 如果有,使用 CUDA 设备 0
else:
device = torch.device('cpu') # 否则,使用 CPU
这段代码的作用是根据是否有可用的 CUDA 设备来选择使用 CUDA 还是 CPU。如果有可用的 CUDA 设备,就将设备设置为 cuda:0,否则设置为 cpu。这样可以在需要使用 GPU 进行计算的情况下自动选择 GPU,否则使用 CPU。3) 读取数据源,代码如下:
# 读取文件并存储为DataFrame
plant = pd.read_csv("./聚类分析/plant.csv")
# 选择需要的列
plant_d = plant[['Sepal_Length', 'Sepal_Width', 'Petal_Length', 'Petal_Width']]
# 将 Species 列重命名为 target
plant['target'] = plant['Species']
# 将数据转换为NumPy数组,然后通过torch.from_numpy将其转换为Torch张量,并将结果存储在x中
x = torch.from_numpy(np.array(plant_d))
# 将目标值转换为 Torch 张量,并将结果存储在y中
y = torch.from_numpy(np.array(plant.target))
这段代码的目的是对数据进行预处理,选择特定的列,并将数据转换为适合 Torch 使用的格式。具体的应用场景和后续处理步骤将取决于代码的整体上下文。4) 设置聚类模型,代码如下:
# 设置聚类数
num_clusters = 3
# 设置聚类模型
cluster_ids_x, cluster_centers = kmeans(
# 输入数据
X=x,
# 聚类数
num_clusters=num_clusters,
# 距离度量方式,这里使用欧几里得距离
distance='euclidean',
# 设备,例如 'cuda' 或 'cpu'
device=device
)
# 输出聚类 ID 和聚类中心点
print(cluster_ids_x)
print(cluster_centers)
这段代码用于执行聚类分析,并输出聚类的 ID 和中心点。具体的聚类结果将根据输入数据和聚类参数的不同而有所变化。5) 绘制聚类后的散点图,代码如下:
#创建一个图形,设置图形大小为4×3英寸,分辨率为160dpi
plt.figure(figsize=(4, 3), dpi=160)
# 在图形上绘制散点图,x轴和y轴的数据分别为x矩阵的第0列和第1列,颜色根据cluster_ids_x进行映射,使用'cool'颜色映射,标记为"D"
plt.scatter(x[:, 0], x[:, 1], c=cluster_ids_x, cmap='cool', marker="D")
# 在图形上绘制聚类中心点的散点图,x 轴和 y 轴的数据分别为 cluster_centers 矩阵的第 0 列和第 1 列,颜色为白色,透明度为 0.6,边缘颜色为黑色,线宽为 2
plt.scatter(
cluster_centers[:, 0], cluster_centers[:, 1],
c='white',
alpha=0.6,
edgecolors='black',
linewidths=2
)
# 自动调整图形布局,使图形元素适当地排列
plt.tight_layout()
# 显示图形
plt.show()
这段代码通常用于数据可视化和聚类分析等任务。通过这段代码,你可以绘制出带有颜色映射和聚类中心点的散点图。具体的图形外观将取决于你的数据和设置的参数。本实验通过花瓣长度、花瓣宽度、花萼长度、花萼宽度4个特征对植物花卉进行了分类。运行建模步骤中的代码,模型的聚类结果如下:
tensor([2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2, 2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2, 2,2,1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1,1,1,1,0,1,0,0,0,0,1,0,0,0,0,0,0,1,1,0,0,0,0,1, 0,1,0,1,0,0,1,1,0,0,0,0,0,1,0,0,0,0,1,0,0,0,1,0, 0,0,1,0,0,1])
聚类分析的聚类中心点如下:
tensor([[6.8500, 3.0737, 5.7421, 2.0711],
[5.9016, 2.7484, 4.3935, 1.4339],
[5.0060, 3.4280, 1.4620, 0.2460]])
带聚类中心点的聚类散点图如下图所示:

图 5 聚类效果图
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: