层次聚类算法详解(Python实现)
系统聚类法(hierarchical clustering method)又叫分层聚类法,是目前最常用的聚类分析方法。
层次聚类是通过计算不同类别点的相似度创建一棵有层次的树结构(见下图),在这棵树中,树的底层是原始数据点,顶层是一个聚类的根节点。
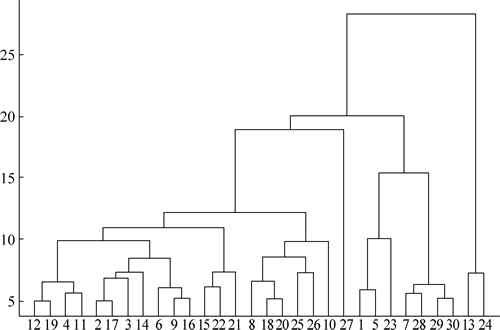
图 1 层次聚类树
创建这样一棵树的方法有自底向上和自顶向下两种。
下面介绍如何利用自底向上的方法构造一棵树。假设有 5 条数据,如下图所示,用这 5 条数据构造一棵树。

图 2 5条数据
首先,计算两两样本之间相似度,然后找到最相似的两条数据(假设 1、2 最相似),接着将其合并起来,成为一条数据,如下图所示。
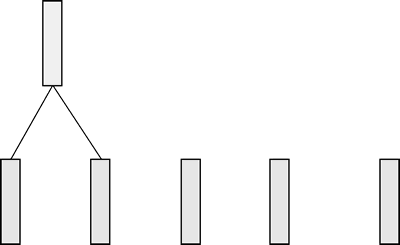
图 3 一条数据
现在数据还剩 4 条,同样计算两两之间的相似度,找出最相似的两条数据(假设前两条最相似),然后合并起来,如下图所示。
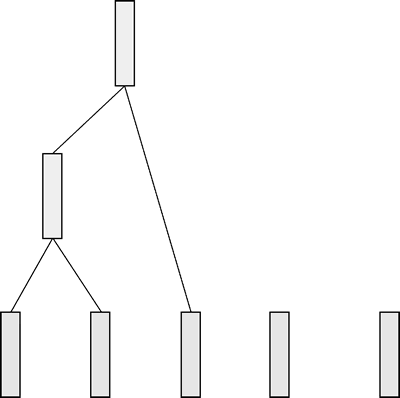
图 4 相似的两条数据
将剩余的 3 条数据继续重复上面的步骤,假设后面两条数据最相似,如下图所示:
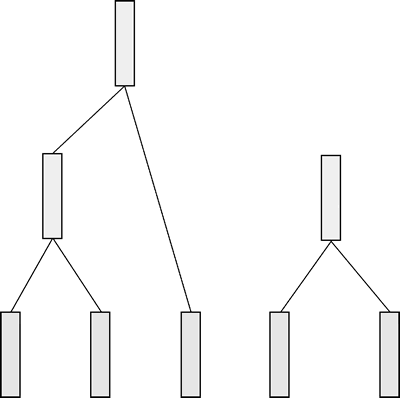
图 5 后两条数据最相似
再把剩余的两条数据合并起来,最终完成一棵树的构建,如下图所示:
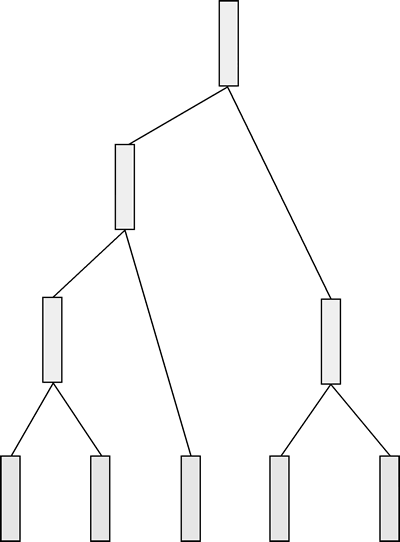
图 6 完成一棵树的构建
以上过程为自底向上聚类树的构建过程,自顶向下的过程与之相似,区别在于:初始数据是一个类别,需要不断分裂出距离最远的那个点,直到所有的点都成为叶节点。
那么如何根据这棵树进行聚类呢?从树的中间部分切一刀,像下图这样:
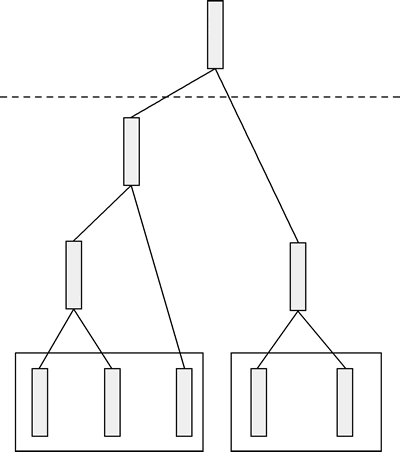
图 7 分割聚类树
接着,叶节点被分成两个类别,也可以像下图所示这样切:
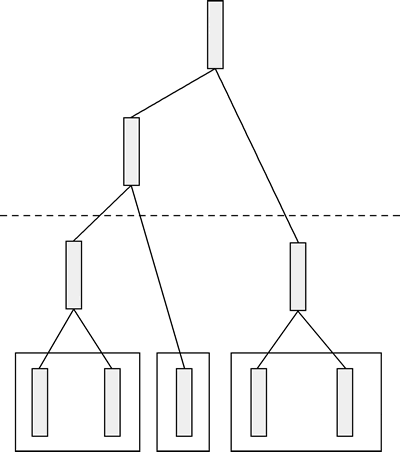
图 8 分成两个类别
这样样本集就被分成 3 个类别。这条切割的线由一个阈值(threshold)来决定切在什么位置,此处的阈值是需要预先给定的。但在实际过程中,往往不需要先构建一棵树,再去进行切分,在建树的过程中当达到所指定的类别后,就可以停止树的建立了。
【实例】实现层次聚类。
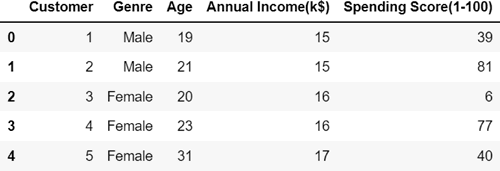
将使用该数据集在 Annual Income(k$)和 Spending Score(1-100)列上实现层次聚类模型,所以需要从数据集中提取这两个特征:
【实例】确定最佳集群数。下面在尝试对数据进行聚类之前,需要知道数据可以最佳地聚类到多少个集群。所以首先在数据集上实现一个树状图来实现这个目标:
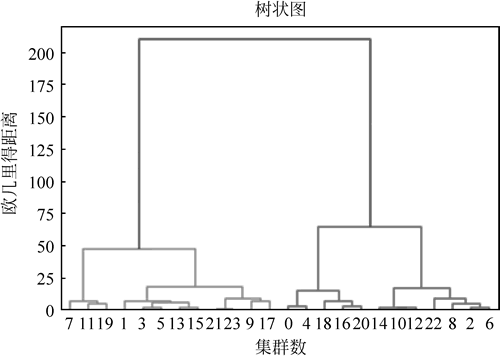
图 10 树状图1
在图 10 中,可以确定最佳聚类数。假设截断整个树状图中的所有水平线,然后找到不与这些假设线相交的最长垂直线。越过那条最长的线,建立一个分界线。可以对数据进行最佳聚类,聚类数等于已建立的阈值所跨越的欧几里得距离(垂直线)的计数。下面训练聚类模型来实现这个目标。
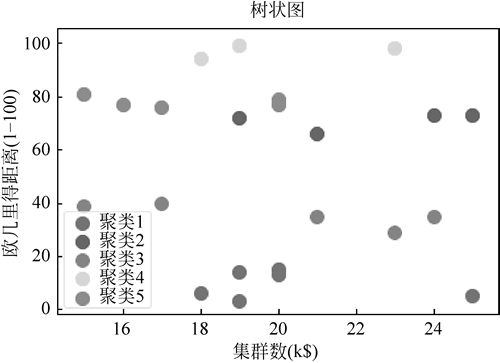
图 11 树状图2
层次聚类是通过计算不同类别点的相似度创建一棵有层次的树结构(见下图),在这棵树中,树的底层是原始数据点,顶层是一个聚类的根节点。

图 1 层次聚类树
创建这样一棵树的方法有自底向上和自顶向下两种。
下面介绍如何利用自底向上的方法构造一棵树。假设有 5 条数据,如下图所示,用这 5 条数据构造一棵树。

图 2 5条数据
首先,计算两两样本之间相似度,然后找到最相似的两条数据(假设 1、2 最相似),接着将其合并起来,成为一条数据,如下图所示。

图 3 一条数据
现在数据还剩 4 条,同样计算两两之间的相似度,找出最相似的两条数据(假设前两条最相似),然后合并起来,如下图所示。

图 4 相似的两条数据
将剩余的 3 条数据继续重复上面的步骤,假设后面两条数据最相似,如下图所示:

图 5 后两条数据最相似
再把剩余的两条数据合并起来,最终完成一棵树的构建,如下图所示:

图 6 完成一棵树的构建
以上过程为自底向上聚类树的构建过程,自顶向下的过程与之相似,区别在于:初始数据是一个类别,需要不断分裂出距离最远的那个点,直到所有的点都成为叶节点。
那么如何根据这棵树进行聚类呢?从树的中间部分切一刀,像下图这样:

图 7 分割聚类树
接着,叶节点被分成两个类别,也可以像下图所示这样切:

图 8 分成两个类别
这样样本集就被分成 3 个类别。这条切割的线由一个阈值(threshold)来决定切在什么位置,此处的阈值是需要预先给定的。但在实际过程中,往往不需要先构建一棵树,再去进行切分,在建树的过程中当达到所指定的类别后,就可以停止树的建立了。
【实例】实现层次聚类。
'''导入相关库'''
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
'''读取数据'''
ourData=pd.read_csv('Mall_Customers.csv')
ourData.head()
运行程序,输出如下:
将使用该数据集在 Annual Income(k$)和 Spending Score(1-100)列上实现层次聚类模型,所以需要从数据集中提取这两个特征:
newData=ourData.iloc[:, [3,4]].values newData运行程序,输出如下:
array([[15,39],
[15,81],
[16,6],
[16,77],
...
[24,73],
[25,5],
[25,73]],dtype=int64)
从结果可以看到数据不一致,必须对数据进行缩放,以使各种特征具有可比性;否则,最终会得到一个劣质的模型。【实例】确定最佳集群数。下面在尝试对数据进行聚类之前,需要知道数据可以最佳地聚类到多少个集群。所以首先在数据集上实现一个树状图来实现这个目标:
# 确定最佳集群数
import matplotlib.pyplot as plt
import scipy.cluster.hierarchy as sch
import numpy as np
# 支持中文与负号
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 假设 newData 已经准备好,例如:
# newData = np.array([[...], [...], ...])
# 绘制树状图
dendrogram = sch.dendrogram(sch.linkage(newData, method='ward'))
plt.title('树状图')
plt.xlabel('样本')
plt.ylabel('欧几里得距离')
plt.show()
运行程序,效果如下图所示:
图 10 树状图1
在图 10 中,可以确定最佳聚类数。假设截断整个树状图中的所有水平线,然后找到不与这些假设线相交的最长垂直线。越过那条最长的线,建立一个分界线。可以对数据进行最佳聚类,聚类数等于已建立的阈值所跨越的欧几里得距离(垂直线)的计数。下面训练聚类模型来实现这个目标。
'''层次聚类模型训练'''
from sklearn.cluster import AgglomerativeClustering
# n_clusters为集群数,affinity指定用于计算距离的度量,linkage参数中的ward为离差平方和法
Agg_hc = AgglomerativeClustering(n_clusters=5, affinity='euclidean', linkage='ward')
y_hc = Agg_hc.fit_predict(newData) #训练数据
'''可视化数据是如何聚集的'''
plt.scatter(newData[y_hc == 0, 0], newData[y_hc == 0, 1], s=100, c='red', label='聚类1')
#聚类1
plt.scatter(newData[y_hc == 1, 0], newData[y_hc == 1, 1], s=100, c='blue', label='聚类2')
#聚类2
plt.scatter(newData[y_hc == 2, 0], newData[y_hc == 2, 1], s=100, c='green', label='聚类3')
#聚类3
plt.scatter(newData[y_hc == 3, 0], newData[y_hc == 3, 1], s=100, c='cyan', label='聚类4')
#聚类4
plt.scatter(newData[y_hc == 4, 0], newData[y_hc == 4, 1], s=100, c='magenta', label='聚类5')
#聚类5
plt.title('树状图')
plt.xlabel('集群数(k$)')
plt.ylabel('欧几里得距离(1-100)')
plt.legend()
plt.show()
运行程序,效果如下图所示:
图 11 树状图2
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: