二叉树的层次遍历(图文并茂,C语言实现)
在二叉树遍历方案中除了有先序遍历、中序遍历和后序遍历,还有层次遍历,即按照层次从左向右遍历。
一棵树如下图所示:
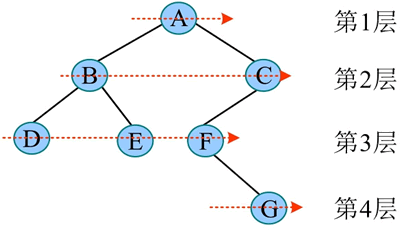
其层次遍历过程:首先遍历第 1 层 A,然后遍历第 2 层,从左向右遍历 B、C,再遍历第 3 层,从左向右遍历 D、E、F,再遍历第 4 层的 G。
程序是怎么实现层次遍历的呢?通过观察可以发现,先被访问的节点,其孩子也先被访问,先来先服务,因此可以用队列实现。
下面以上图所示的二叉树为例,展示其层次遍历过程。
1) 创建一个队列 Q,令根入队(注意:实际上是指向根 A 的指针入队,为了图解方便,将数据入队):

2) 队头元素出队,输出 A,同时令 A 的孩子 B、C 入队(按从左向右的顺序进行,若是普通树,则包含所有孩子):
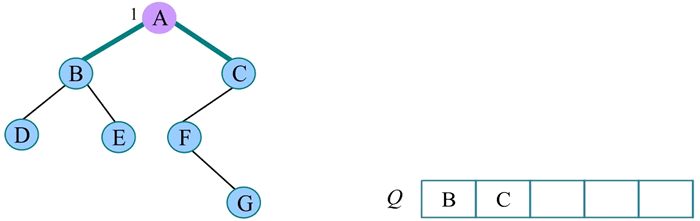
3) 队头元素出队,输出 B,同时令 B 的孩子 D、E 入队:
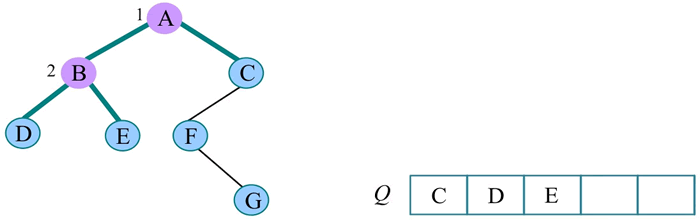
4) 队头元素出队,输出 C,同时令 C 的孩子 F 入队:
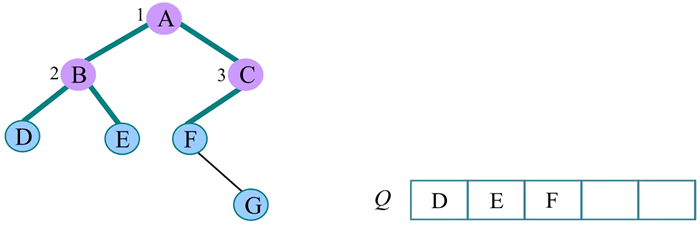
5) 队头元素出队,输出 D,同时令 D 的孩子入队,D 没有孩子,什么也不做:
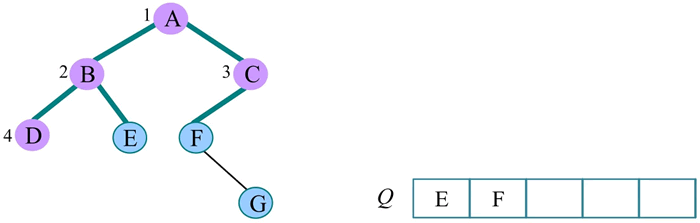
6) 队头元素出队,输出 E,同时令 E 的孩子入队,E 没有孩子,什么也不做:
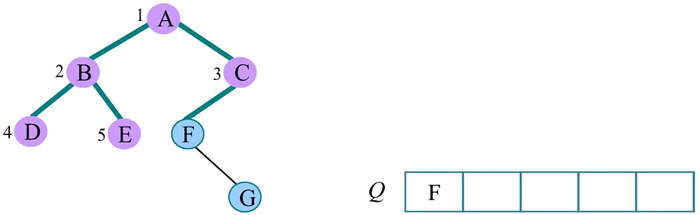
7) 队头元素出队,输出 F,同时令 F 的孩子 G 入队:
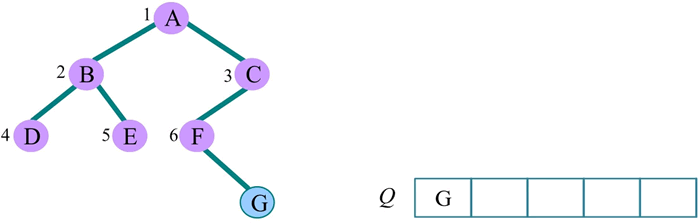
8) 队头元素出队,输出 G,同时令 G 的孩子入队,G 没有孩子,什么也不做。队列为空,算法结束:
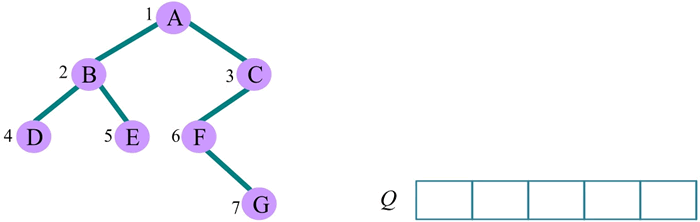
一棵树如下图所示:

其层次遍历过程:首先遍历第 1 层 A,然后遍历第 2 层,从左向右遍历 B、C,再遍历第 3 层,从左向右遍历 D、E、F,再遍历第 4 层的 G。
程序是怎么实现层次遍历的呢?通过观察可以发现,先被访问的节点,其孩子也先被访问,先来先服务,因此可以用队列实现。
下面以上图所示的二叉树为例,展示其层次遍历过程。
1) 创建一个队列 Q,令根入队(注意:实际上是指向根 A 的指针入队,为了图解方便,将数据入队):

2) 队头元素出队,输出 A,同时令 A 的孩子 B、C 入队(按从左向右的顺序进行,若是普通树,则包含所有孩子):

3) 队头元素出队,输出 B,同时令 B 的孩子 D、E 入队:

4) 队头元素出队,输出 C,同时令 C 的孩子 F 入队:

5) 队头元素出队,输出 D,同时令 D 的孩子入队,D 没有孩子,什么也不做:

6) 队头元素出队,输出 E,同时令 E 的孩子入队,E 没有孩子,什么也不做:

7) 队头元素出队,输出 F,同时令 F 的孩子 G 入队:

8) 队头元素出队,输出 G,同时令 G 的孩子入队,G 没有孩子,什么也不做。队列为空,算法结束:

层次遍历的C语言实现
#include <stdio.h>
#include <stdlib.h>
#define TElemType char
#define NODENUM 7
//初始化队头和队尾指针开始时都为0
int front = 0, rear = 0;
typedef struct BiTNode {
TElemType data;//数据域
struct BiTNode* lchild, * rchild;//左右孩子指针
}BiTNode, * BiTree;
// 初始化树的函数
void CreateBiTree(BiTree *T) {
*T = (BiTNode *)malloc(sizeof(BiTNode)); // 创建根节点A
(*T)->data = 'A';
(*T)->lchild = (BiTNode *)malloc(sizeof(BiTNode)); // 创建左子节点B
(*T)->rchild = (BiTNode *)malloc(sizeof(BiTNode)); // 创建右子节点C
(*T)->lchild->data = 'B';
(*T)->lchild->lchild = (BiTNode *)malloc(sizeof(BiTNode)); // 创建B的左子节点D
(*T)->lchild->rchild = (BiTNode *)malloc(sizeof(BiTNode)); // 创建B的右子节点E
(*T)->rchild->data = 'C';
(*T)->rchild->lchild = (BiTNode *)malloc(sizeof(BiTNode)); // 创建C的左子节点F
(*T)->rchild->rchild = NULL; // C的右子节点为空
(*T)->lchild->lchild->data = 'D';
(*T)->lchild->lchild->lchild = NULL;
(*T)->lchild->lchild->rchild = NULL;
(*T)->lchild->rchild->data = 'E';
(*T)->lchild->rchild->lchild = NULL;
(*T)->lchild->rchild->rchild = NULL;
(*T)->rchild->lchild->data = 'F';
(*T)->rchild->lchild->lchild = NULL;
(*T)->rchild->lchild->rchild = (BiTNode *)malloc(sizeof(BiTNode));// 创建F的右子节点G
(*T)->rchild->lchild->rchild->data = 'G';
(*T)->rchild->lchild->rchild->lchild = NULL;
(*T)->rchild->lchild->rchild->rchild = NULL;
}
//入队函数
void EnQueue(BiTree* a, BiTree node) {
if (rear == NODENUM) {
printf("队列已满,入队失败\n");
exit(0);
}
a[rear++] = node;
}
//出队函数
BiTNode* DeQueue(BiTNode** a) {
if (front == rear) {
printf("队列为空,出队失败\n");
exit(0);
}
return a[front++];
}
//层次遍历二叉树
void LevelOrderTraverse(BiTree T) {
//如果二叉树存在,才进行层次遍历
if (T) {
BiTree a[20] = { 0 };
BiTree p = NULL;
p = T;
//根结点入队
EnQueue(a, p);
//重复执行,直至队列为空
while (front < rear)
{
//从队列取出一个结点
p = DeQueue(a);
//访问当前结点
printf("%c ", p->data);
//将当前结点的左右孩子依次入队
if (p->lchild) {
EnQueue(a, p->lchild);
}
if (p->rchild) {
EnQueue(a, p->rchild);
}
}
}
}
//后序遍历二叉树,释放树占用的内存
void DestroyBiTree(BiTree T) {
if (T) {
DestroyBiTree(T->lchild);//销毁左孩子
DestroyBiTree(T->rchild);//销毁右孩子
free(T);//释放结点占用的内存
}
}
int main() {
BiTree Tree;
CreateBiTree(&Tree);
LevelOrderTraverse(Tree);
DestroyBiTree(Tree);
return 0;
}
运行结果为:
A B C D E F G
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: