Java遍历二叉树的3种方法(先序、中序和后序遍历)
在二叉树的应用中,经常需要对二叉树中的每个结点进行访问,即二叉树的遍历。
二叉树的遍历即按照某种规律对二叉树的每个结点进行访问,使得每个结点仅被访问一次。这里的访问可以是对结点的输出、统计结点的个数等。
二叉树的遍历过程其实是将二叉树的非线性序列转换成一个线性序列的过程。二叉树是一种非线性的结构,通过遍历二叉树,按照某种规律对二叉树中的每个结点进行访问且仅访问一次,得到一个顺序序列。
由二叉树的定义可知,二叉树是由根结点、左子树和右子树构成的。如果依次对这 3 部分进行遍历,就完成了整个二叉树的遍历。二叉树的结点的基本结构如下图所示。如果用 D、L、R 分别代表遍历根结点、遍历左子树和遍历右子树,根据组合原理,有 6 种遍历方案:DLR、DRL、LDR、LRD、RDL 和 RLD。
图 1 二叉树的结点的基本结构
若限定先左后右的次序,则在以上 6 种遍历方案中,只剩下 3 种方案:DLR、LDR 和 LRD。其中,DLR 称为先序遍历,LDR 称为中序遍历,LRD 称为后序遍历。
根据二叉树的先序递归定义,得到图 2 所示的二叉树的先序序列为:A、B、D、G、E、H、I、C、F、J。
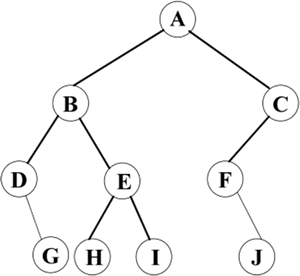
图 2 二叉树
在二叉树先序的遍历过程中,对每一棵二叉树重复执行以上的递归遍历操作,就可以得到先序序列。
例如,在遍历根结点 A 的左子树 {B,D,E,G,H,I} 时,根据先序遍历的递归定义:
根据二叉树的先序递归定义,可以得到二叉树的先序递归算法:
重复执行以上两个步骤,直到栈空为止。以上算法思想的执行流程如下图所示:
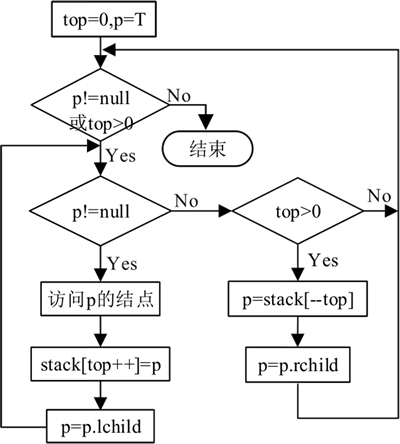
图 3 二叉树的非递归先序遍历执行流程图
二叉树的先序遍历非递归算法实现如下:
根据二叉树的中序递归定义,如图 2 所示的二叉树的中序序列为 D、G、B、H、E、I、A、F、J、C。
在二叉树的中序遍历过程中,对每一棵二叉树重复执行以上递归遍历操作,就可以得到二叉树的中序序列。
例如,如果要中序遍历 A 的左子树 {B,D,E,G,H,I},根据中序遍历的递归定义,先中序遍历 B 的左子树 {D,G},然后访问根结点 B,最后中序遍历 B 的右子树 {E,H,I}。在子树 {D,G} 中,D 是根结点,没有左子树,因此访问根结点 D,接着遍历 D 的右子树,因为右子树只有一个结点 G,所以直接访问 G。
在左子树遍历完毕之后,访问根结点 B。最后要遍历 B 的右子树 {E,H,I},E 是子树 {E,H,I} 的根结点,需要先遍历左子树 {H},因为左子树只有一个 H,所以直接访问 H,然后访问根结点 E,最后遍历右子树 {I},右子树也只有一个结点,所以直接访问 I,B 的右子树访问完毕。因此,A 的左子树的中序序列为 D、G、B、H、E 和 I。
从以上二叉树的中序序列可以看出,A 的左边是 A 的左子树序列,A 的右边是 A 的右子树序列。同样,B 的左边是 B 的左子树序列,B 的右边是 B 的右子树序列。根结点把二叉树的中序序列分为左右两棵子树序列,左边是左子树序列,右边是右子树序列。
根据二叉树的中序递归定义,可以得到二叉树的中序递归算法:
从二叉树的根结点开始,将根结点的指针入栈,执行以下两个步骤:
以上算法思想的执行流程如下图所示:
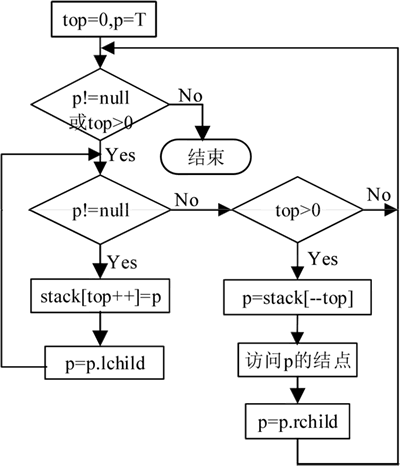
图 4 二叉树的先序遍历非递归实现执行流程图
二叉树中序遍历的非递归算法实现如下:
根据二叉树的后序递归定义,如图 2 所示的二叉树的后序序列为 G、D、H、I、E、B、J、F、C、A。
在二叉树的后序遍历过程中,对每一棵二叉树重复执行以上递归遍历操作,就可以得到二叉树的后序序列。
例如,如果要后序遍历 A 的左子树 {B,D,E,G,H,I},根据后序遍历的递归定义,需要先后序遍历 B 的左子树 {D,G},然后后序遍历 B 的右子树 {E,H,I},最后访问根结点 B。在子树 {D,G} 中,D 是根结点,没有左子树,因此遍历 D 的右子树,因为右子树只有一个结点 G,所以直接访问 G,接着访问根结点 D。
在左子树遍历完毕之后,需要遍历 B 的右子树 {E,H,I},E 是子树 {E,H,I} 的根结点,需要先遍历左子树 {H},因为左子树只有一个 H,所以直接访问 H,然后遍历右子树 {I},右子树也只有一个结点,所以直接访问 I,最后访问子树 {E,H,I} 的根结点 E。此时,B 的左、右子树均访问完毕。最后访问结点 B。因此,A 的左子树的后序序列为 G、D、H、I、E 和 B。
依据二叉树的后序递归定义,可以得到二叉树的后序递归算法:
从二叉树的根结点开始,将根结点的指针入栈,执行以下步骤:
以上算法思想的执行流程如下图所示:
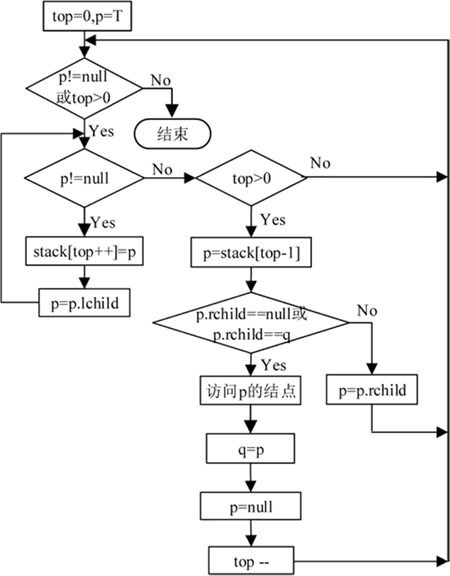
图 5 二叉树后序遍历的非递归实现执行流程图
二叉树后序遍历的非递归算法实现如下:
二叉树的遍历即按照某种规律对二叉树的每个结点进行访问,使得每个结点仅被访问一次。这里的访问可以是对结点的输出、统计结点的个数等。
二叉树的遍历过程其实是将二叉树的非线性序列转换成一个线性序列的过程。二叉树是一种非线性的结构,通过遍历二叉树,按照某种规律对二叉树中的每个结点进行访问且仅访问一次,得到一个顺序序列。
由二叉树的定义可知,二叉树是由根结点、左子树和右子树构成的。如果依次对这 3 部分进行遍历,就完成了整个二叉树的遍历。二叉树的结点的基本结构如下图所示。如果用 D、L、R 分别代表遍历根结点、遍历左子树和遍历右子树,根据组合原理,有 6 种遍历方案:DLR、DRL、LDR、LRD、RDL 和 RLD。

图 1 二叉树的结点的基本结构
若限定先左后右的次序,则在以上 6 种遍历方案中,只剩下 3 种方案:DLR、LDR 和 LRD。其中,DLR 称为先序遍历,LDR 称为中序遍历,LRD 称为后序遍历。
二叉树的先序遍历
二叉树的先序遍历的递归定义如下:- 如果二叉树为空,则执行空操作。如果二叉树非空,则执行以下操作:
- 访问根结点;
- 先序遍历左子树;
- 先序遍历右子树。
根据二叉树的先序递归定义,得到图 2 所示的二叉树的先序序列为:A、B、D、G、E、H、I、C、F、J。

图 2 二叉树
在二叉树先序的遍历过程中,对每一棵二叉树重复执行以上的递归遍历操作,就可以得到先序序列。
例如,在遍历根结点 A 的左子树 {B,D,E,G,H,I} 时,根据先序遍历的递归定义:
- 先访问根结点 B,然后遍历 B 的左子树为 {D,G},最后遍历 B 的右子树为 {E,H,I}。
- 访问过 B 之后,开始遍历 B 的左子树 {D,G},在子树 {D,G} 中,先访问根结点 D,因为 D 没有左子树,所以遍历其右子树,右子树只有一个结点 G,所以访问 G。
- B 的左子树遍历完毕,按照以上方法遍历 B 的右子树。
- 最后得到结点 A 的左子树先序序列:B、D、G、E、H、I。
根据二叉树的先序递归定义,可以得到二叉树的先序递归算法:
public void PreOrderTraverse(BiTreeNode T) // 先序遍历二叉树的递归实现
{
if(T!=null) {
System.out.print(T.data+" "); // 访问根结点
PreOrderTraverse(T.lchild); // 先序遍历左子树
PreOrderTraverse(T.rchild); // 先序遍历右子树
}
}
下面利用栈消除递归,利用非递归实现二叉树的先序遍历。算法实现:从二叉树的根结点开始,访问根结点,然后将根结点的指针入栈,重复执行以下两个步骤:
- 如果该结点的左孩子结点存在,访问左孩子结点,并将左孩子结点的指针入栈,重复执行此操作,直到结点的左孩子不存在。
- 将栈顶的元素(指针)出栈,如果该指针指向的右孩子结点存在,则将当前指针指向右孩子结点。
重复执行以上两个步骤,直到栈空为止。以上算法思想的执行流程如下图所示:

图 3 二叉树的非递归先序遍历执行流程图
二叉树的先序遍历非递归算法实现如下:
public void PreOrderTraverse2(BiTreeNode T) // 先序遍历二叉树的非递归实现
{
BiTreeNode stack[] = new BiTreeNode[MAXSIZE]; // 定义一个栈,用于存放结点的指针
int top = 0; // 定义栈顶指针,初始化栈
BiTreeNode p = T;
while(p != null || top > 0) { // 若 p 不为空,则访问根结点,遍历左子树
while (p != null) {
System.out.print(p.data + " "); // 访问根结点
stack[top++] = p; // 遍历左子树
p = p.lchild; // 遍历左子树
}
if (top > 0) { // 若栈不为空
p = stack[--top]; // 则栈顶元素出栈
p = p.rchild; // 遍历右子树
}
}
}
以上算法直接利用数组来模拟栈的实现,当然也可以定义一个栈类型实现。二叉树的中序遍历
二叉树的中序遍历的递归定义如下:- 若二叉树为空,则执行空操作。若二叉树非空,则执行以下操作;
- 中序遍历左子树;
- 访问根结点;
- 中序遍历右子树。
根据二叉树的中序递归定义,如图 2 所示的二叉树的中序序列为 D、G、B、H、E、I、A、F、J、C。
在二叉树的中序遍历过程中,对每一棵二叉树重复执行以上递归遍历操作,就可以得到二叉树的中序序列。
例如,如果要中序遍历 A 的左子树 {B,D,E,G,H,I},根据中序遍历的递归定义,先中序遍历 B 的左子树 {D,G},然后访问根结点 B,最后中序遍历 B 的右子树 {E,H,I}。在子树 {D,G} 中,D 是根结点,没有左子树,因此访问根结点 D,接着遍历 D 的右子树,因为右子树只有一个结点 G,所以直接访问 G。
在左子树遍历完毕之后,访问根结点 B。最后要遍历 B 的右子树 {E,H,I},E 是子树 {E,H,I} 的根结点,需要先遍历左子树 {H},因为左子树只有一个 H,所以直接访问 H,然后访问根结点 E,最后遍历右子树 {I},右子树也只有一个结点,所以直接访问 I,B 的右子树访问完毕。因此,A 的左子树的中序序列为 D、G、B、H、E 和 I。
从以上二叉树的中序序列可以看出,A 的左边是 A 的左子树序列,A 的右边是 A 的右子树序列。同样,B 的左边是 B 的左子树序列,B 的右边是 B 的右子树序列。根结点把二叉树的中序序列分为左右两棵子树序列,左边是左子树序列,右边是右子树序列。
根据二叉树的中序递归定义,可以得到二叉树的中序递归算法:
public void InOrderTraverse(BiTreeNode T) // 中序遍历二叉树的递归实现
{
if(T!=null) {
InOrderTraverse(T.lchild); // 中序遍历左子树
System.out.print(T.data+" "); // 访问根结点
InOrderTraverse(T.rchild); // 中序遍历右子树
}
}
下面介绍二叉树中序遍历的非递归算法实现。从二叉树的根结点开始,将根结点的指针入栈,执行以下两个步骤:
- 若该结点的左孩子结点存在,则将左孩子结点的指针入栈。重复执行此操作,直到结点的左孩子不存在。
- 将栈顶的元素(指针)出栈,并访问该指针指向的结点,若该指针指向的右孩子结点存在,则将当前指针指向右孩子结点。重复执行步骤 ① 和步骤 ②,直到栈空为止。
以上算法思想的执行流程如下图所示:

图 4 二叉树的先序遍历非递归实现执行流程图
二叉树中序遍历的非递归算法实现如下:
public void InOrderTraverse2(BiTreeNode T) // 中序遍历二叉树的非递归实现
{
BiTreeNode stack[] = new BiTreeNode[MAXSIZE]; // 定义一个栈,用于存放结点的指针
int top = 0; // 定义栈顶指针,初始化栈
BiTreeNode p = T;
while (p != null || top > 0) { // 若 p 不为空,则遍历左子树
while (p != null) {
stack[top++] = p; // 将 p 入栈
p = p.lchild; // 遍历左子树
}
if (top > 0) { // 若栈不为空
p = stack[--top]; // 则栈顶元素出栈
System.out.print(p.data + " "); // 访问根结点
p = p.rchild; // 遍历右子树
}
}
}
二叉树的后序遍历
二叉树的后序遍历的递归定义如下:- 若二叉树为空,则执行空操作。若二叉树非空,则执行以下操作;
- 后序遍历左子树;
- 后序遍历右子树;
- 访问根结点。
根据二叉树的后序递归定义,如图 2 所示的二叉树的后序序列为 G、D、H、I、E、B、J、F、C、A。
在二叉树的后序遍历过程中,对每一棵二叉树重复执行以上递归遍历操作,就可以得到二叉树的后序序列。
例如,如果要后序遍历 A 的左子树 {B,D,E,G,H,I},根据后序遍历的递归定义,需要先后序遍历 B 的左子树 {D,G},然后后序遍历 B 的右子树 {E,H,I},最后访问根结点 B。在子树 {D,G} 中,D 是根结点,没有左子树,因此遍历 D 的右子树,因为右子树只有一个结点 G,所以直接访问 G,接着访问根结点 D。
在左子树遍历完毕之后,需要遍历 B 的右子树 {E,H,I},E 是子树 {E,H,I} 的根结点,需要先遍历左子树 {H},因为左子树只有一个 H,所以直接访问 H,然后遍历右子树 {I},右子树也只有一个结点,所以直接访问 I,最后访问子树 {E,H,I} 的根结点 E。此时,B 的左、右子树均访问完毕。最后访问结点 B。因此,A 的左子树的后序序列为 G、D、H、I、E 和 B。
依据二叉树的后序递归定义,可以得到二叉树的后序递归算法:
public void PostOrderTraverse(BiTreeNode T) // 后序遍历二叉树的递归实现
{
if(T!=null) { // 如果二叉树不为空
PostOrderTraverse(T.lchild); // 后序遍历左子树
PostOrderTraverse(T.rchild); // 后序遍历右子树
System.out.print(T.data+" "); // 访问根结点
}
}
下面介绍二叉树后序遍历的非递归算法实现。从二叉树的根结点开始,将根结点的指针入栈,执行以下步骤:
- 若该结点的左孩子结点存在,则将左孩子结点的指针入栈。重复执行此操作,直到结点的左孩子不存在。
- 取栈顶元素(指针)并赋给 p,若 p.rchild==null 或 p.rchild=q,即 p 没有右孩子或右孩子结点已经访问过,则访问根结点,即 p 指向的结点,并用 q 记录刚刚访问过的结点指针,将栈顶元素退栈。若 p 有右孩子且右孩子结点没有被访问过,则执行 p=p.rchild。
- 重复执行步骤 ① 和步骤 ②,直到栈空为止。
以上算法思想的执行流程如下图所示:

图 5 二叉树后序遍历的非递归实现执行流程图
二叉树后序遍历的非递归算法实现如下:
public void PostOrderTraverse2(BiTreeNode T) // 后序遍历二叉树的非递归实现
{
BiTreeNode stack[] = new BiTreeNode[MAXSIZE]; // 定义一个栈,用于存放结点指针
int top = 0;
BiTreeNode p = T; // 初始化结点的指针
BiTreeNode q = null;
while (p != null || top > 0) { // 若 p 不为空,则遍历左子树
while (p != null) {
stack[top++] = p; // 将 p 入栈
p = p.lchild; // 遍历左子树
}
if (top > 0) { // 若栈不为空
p = stack[--top]; // 则取栈顶元素
if(p.rchild == null || p.rchild == q) { // 若 p 没有右孩子结点,或右孩子结点已经访问过
System.out.print(p.data+" "); // 则访问根结点
q = p; // 记录刚刚访问过的结点
p = null; // 为遍历右子树做准备
top--; // 出栈
}
else
p = p.rchild;
}
}
}
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: