Java实现二叉树的线索化(非常详细)
在二叉树中,采用二叉链表作为存储结构,只能找到结点的左孩子结点和右孩子结点。要想找到结点的直接前驱或者直接后继,必须对二叉树进行遍历,但这并不是最直接、最简便的方法。通过对二叉树线索化,可以很方便地找到结点的直接前驱和直接后继。
为了能够在二叉树的遍历过程中直接找到结点的直接前驱或者直接后继,可在二叉链表结点中增加两个指针域:一个用来指向结点的前驱,另一个用来指向结点的后继。但这样做需要为结点增加更多的存储单元,使结点结构的利用率大大下降。
在二叉链表的存储结构中,具有 n 个结点的二叉链表有 n+1 个空指针域。由此,可以利用这些空指针域存放结点的直接前驱和直接后继的信息。我们可以做以下规定:
为了区分指针域指向的是左孩子结点还是直接前驱结点,右孩子结点还是直接后继结点,增加两个标志域 ltag 和 rtag。结点的存储结构如下图所示。

图 1 结点的存储结构
其中,当 ltag=0 时,lchild 指向结点的左孩子;当 ltag=1 时,lchild 指向结点的直接前驱结点。当 rtag=0 时,rchild 指向结点的右孩子;当 rtag=1 时,rchild 指向结点的直接后继结点。
由这种存储结构构成的二叉链表称为线索二叉树。采用这种存储结构的二叉链表称为线索链表。其中,指向结点直接前驱和直接后继的指针称为线索。
在二叉树的先序遍历过程中,加上线索之后,得到先序线索二叉树。同理,在二叉树的中序(后序)遍历过程中,加上线索之后,得到中序(后序)线索二叉树。二叉树按照某种遍历方式使二叉树变为线索二叉树的过程称为二叉树的线索化。
如下图所示就是将二叉树进行先序、中序和后序遍历得到的线索二叉树。
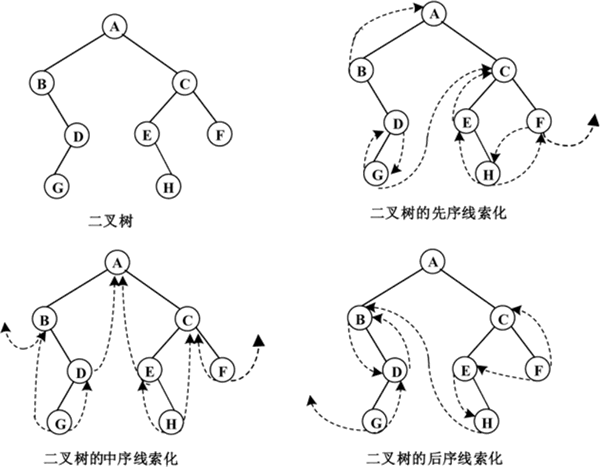
图 2 二叉树的线索化
线索二叉树的存储结构类型描述如下:
因此,二叉树的线索化就是对二叉树的遍历过程。这里以二叉树的中序线索化为例介绍二叉树的线索化。
为了方便,在二叉树线索化时可增加一个头结点。使头结点的指针域 lchild 指向二叉树的根结点,指针域 rchild 指向二叉树中序遍历时的最后一个结点,二叉树中的第一个结点的线索指针指向头结点。初始化时,使二叉树的头结点的 rchild 指针域指向自身,并将头结点的标志域 ltag 置为 Link,标志域 rtag 置为 Thread。
线索化以后的二叉树类似于一个循环链表,操作线索二叉树就像操作循环链表一样,既可以从线索二叉树中的第一个结点开始,根据结点的后继线索指针遍历整棵二叉树,又可以从线索二叉树的最后一个结点开始,根据结点的前驱线索指针遍历整棵二叉树。
经过线索化的二叉树及其存储结构如下图所示:
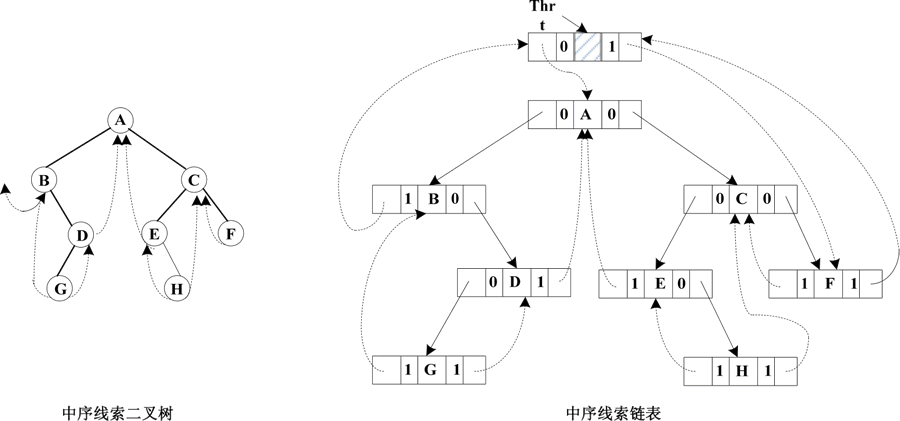
图 3 中序线索二叉树及其链表
中序线索二叉树的算法实现如下:
为了能够在二叉树的遍历过程中直接找到结点的直接前驱或者直接后继,可在二叉链表结点中增加两个指针域:一个用来指向结点的前驱,另一个用来指向结点的后继。但这样做需要为结点增加更多的存储单元,使结点结构的利用率大大下降。
在二叉链表的存储结构中,具有 n 个结点的二叉链表有 n+1 个空指针域。由此,可以利用这些空指针域存放结点的直接前驱和直接后继的信息。我们可以做以下规定:
- 若结点存在左子树,则指针域 lchild 指示其左孩子结点,否则指针域 lchild 指示其直接前驱结点;
- 若结点存在右子树,则指针域 rchild 指示其右孩子结点,否则指针域 rchild 指示其直接后继结点。
为了区分指针域指向的是左孩子结点还是直接前驱结点,右孩子结点还是直接后继结点,增加两个标志域 ltag 和 rtag。结点的存储结构如下图所示。

图 1 结点的存储结构
其中,当 ltag=0 时,lchild 指向结点的左孩子;当 ltag=1 时,lchild 指向结点的直接前驱结点。当 rtag=0 时,rchild 指向结点的右孩子;当 rtag=1 时,rchild 指向结点的直接后继结点。
由这种存储结构构成的二叉链表称为线索二叉树。采用这种存储结构的二叉链表称为线索链表。其中,指向结点直接前驱和直接后继的指针称为线索。
在二叉树的先序遍历过程中,加上线索之后,得到先序线索二叉树。同理,在二叉树的中序(后序)遍历过程中,加上线索之后,得到中序(后序)线索二叉树。二叉树按照某种遍历方式使二叉树变为线索二叉树的过程称为二叉树的线索化。
如下图所示就是将二叉树进行先序、中序和后序遍历得到的线索二叉树。

图 2 二叉树的线索化
线索二叉树的存储结构类型描述如下:
class BiThrNode // 线索二叉树的结点
{
String data; // 二叉树的结点值
BiThrNode lchild, rchild; // 左孩子,右孩子
int ltag, rtag; // 线索标志域
BiThrNode(String data, BiThrNode lchild, BiThrNode rchild, int ltag, int rtag) {
this.data = data; // 二叉树的结点值
this.lchild = lchild; // 左孩子
this.rchild = rchild; // 右孩子
this.ltag = ltag; // 线索标志域
this.rtag = rtag; // 线索标志域
}
BiThrNode(String data) {
this.data = data; // 二叉树的结点值
this.lchild = null; // 左孩子
this.rchild = null; // 右孩子
this.ltag = 0; // 线索标志域
this.rtag = 0; // 线索标志域
}
}
二叉树的线索化算法实现
二叉树的线索化就是利用二叉树中结点的空指针域表示结点的前驱信息或后继信息。而要得到结点的前驱信息和后继信息,需要对二叉树进行遍历,同时将结点的空指针域修改为其直接前驱或直接后继信息。因此,二叉树的线索化就是对二叉树的遍历过程。这里以二叉树的中序线索化为例介绍二叉树的线索化。
为了方便,在二叉树线索化时可增加一个头结点。使头结点的指针域 lchild 指向二叉树的根结点,指针域 rchild 指向二叉树中序遍历时的最后一个结点,二叉树中的第一个结点的线索指针指向头结点。初始化时,使二叉树的头结点的 rchild 指针域指向自身,并将头结点的标志域 ltag 置为 Link,标志域 rtag 置为 Thread。
线索化以后的二叉树类似于一个循环链表,操作线索二叉树就像操作循环链表一样,既可以从线索二叉树中的第一个结点开始,根据结点的后继线索指针遍历整棵二叉树,又可以从线索二叉树的最后一个结点开始,根据结点的前驱线索指针遍历整棵二叉树。
经过线索化的二叉树及其存储结构如下图所示:

图 3 中序线索二叉树及其链表
中序线索二叉树的算法实现如下:
public BiThrNode InOrderThreading(BiThrNode T) // 通过中序遍历二叉树 T,使 T 中序线索化。thrt 是指向头结点的指针
{
BiThrNode thrt = new BiThrNode(); // 将头结点线索化
thrt.ltag = 0; // 修改前驱线索标志
thrt.rtag = 1; // 修改后继线索标志
thrt.rchild = thrt; // 将头结点的 rchild 指针指向自己
if (T == null) // 若二叉树为空,则将 lchild 指针指向自己
thrt.lchild = thrt;
else {
thrt.lchild = T; // 将头结点的左指针指向根结点
pre = thrt; // 将 pre 指向已经线索化的结点
pre = InThreading(T); // 中序遍历进行中序线索化
// 将最后一个结点线索化
pre.rchild = thrt; // 将最后一个结点的右指针指向头结点
pre.rtag = 1; // 修改最后一个结点的 rtag 标志域
thrt.rchild = pre; // 将头结点的 rchild 指针指向最后一个结点
thrt.lchild = T; // 将头结点的左指针指向根结点
}
return thrt;
}
public BiThrNode InThreading(BiThrNode p) { // 二叉树中序线索化
if (p != null) { // 左子树线索化
InThreading(p.lchild);
if (p.lchild == null) { // 前驱线索化
p.ltag = 1;
p.lchild = pre;
}
if (pre.rchild == null) { // 后继线索化
pre.rtag = 1;
pre.rchild = p;
}
pre = p; // pre 指向的结点线索化完毕,使 p 指向的结点成为前驱
InThreading(p.rchild); // 右子树线索化
}
return p;
}
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: