层次聚类算法(非常详细,附带实例)
层次聚类是聚类算法的一种,通过计算不同类别数据点间的相似度来创建一棵有层次的嵌套聚类树,如下图所示。
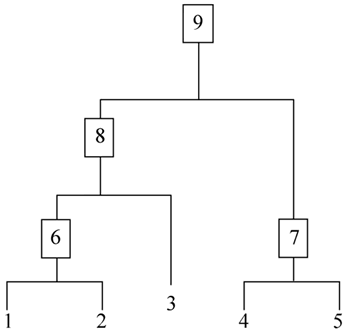
图 1 聚类树
在聚类树中,不同类别的原始数据点是树的最底层,树的顶层是一个聚类的根节点。层次聚类算法相比划分聚类算法的优点之一是可以在不同的尺度上(层次)展示数据集的聚类情况。
创建聚类树有两种方式:自下而上和自上而下。基于层次的聚类算法可以分为凝聚的(agglomerative)或者分裂的(divisive)。
简单地说层次聚类的合并算法是通过计算每一个类别的数据点与所有数据点之间的距离来确定它们之间的相似性,距离越小,相似度越高。并将距离最近的两个数据点或类别进行组合,生成聚类树。
绝大多数层次聚类属于凝聚型层次聚类,它的算法流程如下(见下图):
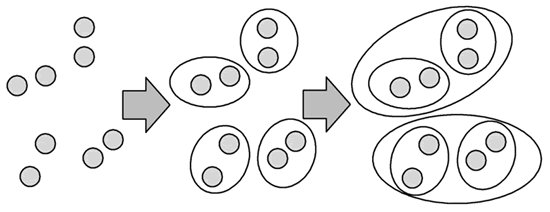
图 2 自底向上的层次算法过程
整个过程就是建立一棵树,在建立的过程中,可以在步骤 4 设置所需分类的类别个数,作为迭代的终止条件,如果都归为一类并不实际。
层次聚类使用欧氏距离来计算不同类别数据点间的距离(相似度):

使用平均连接计算组合数据点间的距离。下面是计算组合数据点 (A, F) 到 (B,C) 的距离,这里分别计算了 (A, F) 和 (B, C)两两间距离的均值。

【实例】利用层次聚类法对给定的数据进行聚类。
当 s 和 t 形成一个新的聚类簇 u 时,s 和 t 从森林(已经形成的聚类簇群)中移除,用新的聚类簇 u 代替。当森林中只有一个聚类簇时算法停止,而这个聚类簇就成了聚类树的根。
距离矩阵在每次迭代中都将被保存,d[i,j] 对应于第 i 个聚类簇与第 j 个聚类簇之间的距离。每次迭代必须更新新形成的聚类簇之间的距离矩阵。
linkage() 函数的格式为:
其他的 method 还有 weighted、centroid 等。函数返回 (n-1)∗4 的矩阵 Z。
【实例】利用 Scipy 库中的层次聚类法对给定数据进行聚类。

图 5 聚类树
以上结果 Z 共有四列:

图 1 聚类树
在聚类树中,不同类别的原始数据点是树的最底层,树的顶层是一个聚类的根节点。层次聚类算法相比划分聚类算法的优点之一是可以在不同的尺度上(层次)展示数据集的聚类情况。
创建聚类树有两种方式:自下而上和自上而下。基于层次的聚类算法可以分为凝聚的(agglomerative)或者分裂的(divisive)。
- 自下而上法:一开始每个个体(object)都是一个类,然后根据 linkage 寻找同类,最后形成一个“类”;
- 自上而下法:一开始所有个体都属于一个“类”,然后根据 linkage 排除异己,最后每个个体都成为一个“类”。
自底向上的层次算法
层次聚类的合并算法通过计算两类数据点间的相似性,对所有数据点中最为相似的两个数据点进行组合,并反复迭代这一过程。简单地说层次聚类的合并算法是通过计算每一个类别的数据点与所有数据点之间的距离来确定它们之间的相似性,距离越小,相似度越高。并将距离最近的两个数据点或类别进行组合,生成聚类树。
绝大多数层次聚类属于凝聚型层次聚类,它的算法流程如下(见下图):
- 将每个对象看作一类,计算两两之间的距离;
- 将距离最小的两个类合并成一个新类;
- 重新计算新类与所有类之间的距离;
- 重复步骤 2、3,直到所有类最后合并成一类。

图 2 自底向上的层次算法过程
整个过程就是建立一棵树,在建立的过程中,可以在步骤 4 设置所需分类的类别个数,作为迭代的终止条件,如果都归为一类并不实际。
层次聚类使用欧氏距离来计算不同类别数据点间的距离(相似度):

聚类间的相似度
计算两个组合数据点间距离的方法有三种,分别为单连接、全连接和平均连接。在开始计算之前,先介绍这三种计算方法及其优缺点。- 单连接(single linkage):将两个组合数据点中距离最近的两个数据点间的距离作为这两个组合数据点的距离。这种方法容易受到极端值的影响。两个很相似的组合数据点可能由于其中的某个极端的数据点距离较近而组合在一起;
- 全连接(complete linkage):与单连接相反,将两个组合数据点中距离最远的两个数据点间的距离作为这两个组合数据点的距离。其问题也与单连接相反,即两个不相似的组合数据点可能由于其中的极端值距离较远而无法组合在一起;
- 平均连接(average linkage):计算两个组合数据点中的每个数据点与其他所有数据点的距离。将所有距离的均值作为两个组合数据点间的距离。这种方法计算量比较大,但结果比前两种方法更合理。
使用平均连接计算组合数据点间的距离。下面是计算组合数据点 (A, F) 到 (B,C) 的距离,这里分别计算了 (A, F) 和 (B, C)两两间距离的均值。

层次聚类实战
前面已对层次聚类的算法、相似度进行了介绍,下面通过实例来演示层次聚类实战。【实例】利用层次聚类法对给定的数据进行聚类。
import math
import numpy as np
import sklearn
from sklearn.datasets import load_iris
def euler_distance(point1: np.ndarray, point2: list) -> float:
"""
计算两点之间的欧式距离,支持多维
"""
distance = 0.0
for a, b in zip(point1, point2):
distance += math.pow(a - b, 2)
return math.sqrt(distance)
class ClusterNode(object):
def __init__(self, vec, left = None, right = None, distance = -1, id = None, count = 1):
"""
:param vec: 保存两个数据聚类后形成新的中心
:param left: 左节点
:param right: 右节点
:param distance: 两个节点的距离
:param id: 用来标记哪些节点是计算过的
:param count: 这个节点的叶节点个数
"""
self.vec = vec
self.left = left
self.right = right
self.distance = distance
self.id = id
self.count = count
class Hierarchical(object):
def __init__(self, k = 1):
assert k > 0
self.k = k
self.labels = None
def fit(self, x):
nodes = [ClusterNode(vec = v, id = i) for i, v in enumerate(x)]
distances = {}
point_num, future_num = np.shape(x) # 特征的维度
self.labels = [ -1 ] * point_num
currentclustid = -1
while len(nodes) > self.k:
min_dist = math.inf
nodes_len = len(nodes)
for i in range(nodes_len - 1):
for j in range(i + 1, nodes_len):
# 为了不重复计算距离,保存在字典内
d_key = (nodes[i].id, nodes[j].id)
if d_key not in distances:
distances[d_key] = euler_distance(nodes[i].vec, nodes[j].vec)
d = distances[d_key]
if d < min_dist:
min_dist = d
closest_part = (i, j)
# 合并两个聚类
part1, part2 = closest_part
node1, node2 = nodes[part1], nodes[part2]
new_vec = [ (node1.vec[i] * node1.count + node2.vec[i] * node2.count) / (node1.count + node2.count)
for i in range(future_num) ] # #??
new_node = ClusterNode(vec = new_vec,
left = node1,
right = node2,
distance = min_dist,
id = currentclustid,
count = node1.count + node2.count)
currentclustid -= 1
del nodes[part2], nodes[part1]
nodes.append(new_node) # 一定要先 del 索引较大的
self.nodes = nodes
self.calc_label()
def calc_label(self):
"""
调取聚类的结果
"""
for i, node in enumerate(self.nodes):
# 将节点的所有叶节点都分类
self.leaf_traversal(node, i)
def leaf_traversal(self, node: ClusterNode, label):
"""
递归遍历叶节点
"""
if node.left == None and node.right == None:
self.labels[node.id] = label
if node.left:
self.leaf_traversal(node.left, label)
if node.right:
self.leaf_traversal(node.right, label)
if __name__ == '__main__':
data = [[16.9,0],[38.5,0],[39.5,0],[80.8,0],[82,0],[834.6,0],[116.1,0]]
my = Hierarchical(4)
my.fit(data)
print('层次聚类效果:', np.array(my.labels))
运行程序,输出如下:
层次聚类效果:[3 3 3 2 2 0 1]
使用Scipy库中的层次聚类
linkage() 方法用于计算两个聚类簇 s 和 t 之间的距离 d(s, t),这个方法的使用在层次聚类之前。当 s 和 t 形成一个新的聚类簇 u 时,s 和 t 从森林(已经形成的聚类簇群)中移除,用新的聚类簇 u 代替。当森林中只有一个聚类簇时算法停止,而这个聚类簇就成了聚类树的根。
距离矩阵在每次迭代中都将被保存,d[i,j] 对应于第 i 个聚类簇与第 j 个聚类簇之间的距离。每次迭代必须更新新形成的聚类簇之间的距离矩阵。
linkage() 函数的格式为:
linkage(y,method = 'single',metric = 'euclidean')
其中,各参数含义:- y:距离矩阵,可以是一维压缩向量(距离向量),也可以是二维观测向量(坐标矩阵)。如果 y 是一维压缩向量,则 y 必须是 n 个初始观测值的组合,n 是坐标矩阵中成对的观测值;
-
method:指计算类间距离的方法,常用的有 3 种:
- single:最近邻,把类与类间距离最近的作为类间距。
- complete:最远邻,把类与类间距离最远的作为类间距。
- average:平均距离,类与类间所有 pairs 距离的平均。
其他的 method 还有 weighted、centroid 等。函数返回 (n-1)∗4 的矩阵 Z。
【实例】利用 Scipy 库中的层次聚类法对给定数据进行聚类。
#导入相应的包
import scipy
import scipy.cluster.hierarchy as sch
from scipy.cluster.vq import vq,kmeans,whiten
import numpy as np
import matplotlib.pylab as plt
#生成待聚类的数据点,这里生成了20个点,每个点4维:
data = [[16.9,0],[38.5,0],[39.5,0],[80.8,0],[82,0],[834.6,0],[116.1,0]]
#加一个标签进行区分
A = []
for i in range(len(data)):
a = chr(i + ord('A'))
A.append(a)
'''层次聚类'''
#生成点与点之间的距离矩阵,这里用的欧氏距离:
disMat = sch.distance.pdist(data,'euclidean')
#进行层次聚类:
Z = sch.linkage(disMat,method = 'average')
#将层级聚类结果以树状图表示出来并保存为plot_dendrogram.png
fig = plt.figure()
P = sch.dendrogram(Z,labels = A)
f = sch.fcluster(Z,t = 30,criterion = 'distance') #聚类,这里t阈值的选择很重要
print('打印类标签:',f) #打印类标签
print('打印Z值:',Z)
plt.show()
运行程序,输出如下:
打印类标签:[1 1 1 2 2 4 3]
打印Z值:[[ 1. 2. 1. 2. ]
[ 3. 4. 1.2 2. ]
[ 0. 7. 22.1 3. ]
[ 6. 8. 34.7 3. ]
[ 9. 10. 61.33333333 6. ]
[ 5. 11. 772.3 7. ]]
效果如下图所示:
图 5 聚类树
以上结果 Z 共有四列:
- 第一、二列:聚类簇的编号,在初始距离前每个初始值被从 0~n-1 进行标识,每生成一个新的聚类簇就在此基础上增加一对新的聚类簇进行标识;
- 第三列表示前两个聚类簇之间的距离;
- 第四列表示新生成聚类簇所包含的元素的个数。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: