DBSCAN聚类算法详解(Python实现)
DBSCAN 算法是一种基于密度的聚类算法,这类密度聚类算法一般假定类别可以通过样本分布的紧密程度决定。同一类别的样本,它们之间是紧密相连的,也就是说,在该类别任意样本周围一定有同类别的样本存在。
通过将紧密相连的样本划为一类,这样就得到了一个聚类类别。通过将所有各组紧密相连的样本划为各个不同的类别,就得到了最终的所有聚类类别结果。
下图为 DBSCAN 算法概念的相关效果:
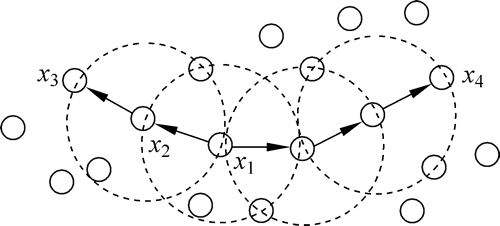
图 1 DBSCAN算法概念的相关效果
图中的 x1 为核心对象;x2 由 x1 密度直达;x3 由 x1 密度可达;x3 与 x4 密度相连。
作为一种算法,DBSCAN 算法也存在缺点,主要表现在:
【实例】 DBSCAN 聚类算法的 Python 实现。
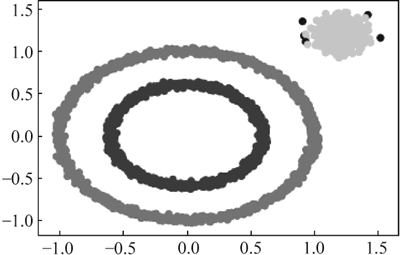
图 2 DBSCAN聚类效果
利用 sklearn 中的 DBSCAN 类进行实现,代码为:
通过将紧密相连的样本划为一类,这样就得到了一个聚类类别。通过将所有各组紧密相连的样本划为各个不同的类别,就得到了最终的所有聚类类别结果。
DBSCAN算法相关概念
首先需要了解与 DBSCAN 有关的几个概念。- ε-邻域:一个对象在半径为 ε 内的区域,简单来说就是以给定的一个数据为圆心画一个半径为 ε 的圆。
- 核心对象(core object):如果 xj 的 ε- 邻域至少包含 minPts 个样本,即 |Nε(xj)|≥minPts,则 xj 是一个核心对象。
- 密度直达(directly density-reachable):如果 xj 位于 xi 的 ε 邻域中,且 xi 是核心对象,则称 xj 由 xi 密度直达。
- 密度可达(density-reachable):对 xi 与 xj,如果存在样本序列 p1,p2,…,pn,其中 p1=xi,pn=xj 且 pi+1 由 pi 密度直达,则称 xj 由 xi 密度可达。
- 密度相连(density-connected):对 xi 与 xj,如果存在 xk 使得 xi 与 xj 均由 xk 密度可达,则称 xi 与 xj 密度相连。
- 簇:基于密度聚类的簇就是最大的密度相连的所有对象的集合。
- 噪声点:不属于任何簇中的对象称为噪声点。
下图为 DBSCAN 算法概念的相关效果:

图 1 DBSCAN算法概念的相关效果
图中的 x1 为核心对象;x2 由 x1 密度直达;x3 由 x1 密度可达;x3 与 x4 密度相连。
DBSCAN算法的优缺点
DBSCAN 算法的优点主要表现在:- 与 K-Means 算法相比,不需要手动确定簇的个数 K,但需要确定邻域 r 和密度阈值 minPts;
- 能发现任意形状的簇;
- 能有效处理噪声点(邻域 r 和密度阈值 minPts 参数的设置可以影响噪声点)。
作为一种算法,DBSCAN 算法也存在缺点,主要表现在:
- 在创建树的过程中要计算每个样本间的距离,计算复杂度较高;
- 算法对于异常值比较敏感,影响聚类效果;
- 容易形成链状的簇。
DBSCAN算法实现
前面已对 DBSCAN 算法的相关概念、优缺点进行了介绍,下面通过实例来演示 DBSCAN 算法的实现。【实例】 DBSCAN 聚类算法的 Python 实现。
from sklearn import datasets
import numpy as np
import random
import matplotlib.pyplot as plt
import time
import copy
# def定义函数+函数名(参数),返回值:return()
def find_neighbor(j, x, eps):
N = list()
for i in range(x.shape[0]):
temp = np.sqrt(np.sum(np.square(x[j] - x[i]))) # 计算欧氏距离
# 如果距离小于eps
if temp <= eps:
# append用于在列表末尾添加新的对象
N.append(i)
# 返回邻居的索引
return set(N)
def DBSCAN(X, eps, min_Pts):
k = -1
neighbor_list = [] # 用来保存每个数据的邻域
omega_list = [] # 核心对象集合
gama = set([x for x in range(len(X))]) # 初始时将所有点标记为未访问
cluster = [-1 for _ in range(len(X))] # 聚类
for i in range(len(X)):
neighbor_list.append(find_neighbor(i, X, eps))
# 取倒数第一个进行判断,如果大于设定的样本数,即为核心点
if len(neighbor_list[-1]) >= min_Pts:
omega_list.append(i) # 将样本加入核心对象集合
omega_list = set(omega_list) # 转换为集合便于操作
while len(omega_list) > 0:
# 深复制gama
gama_old = copy.deepcopy(gama)
j = random.choice(list(omega_list)) # 随机选取一个核心对象
# k计数,从0开始
k = k + 1
# 初始化Q
Q = list()
# 记录访问点
Q.append(j)
# 从gama中移除j,剩余未访问点
gama.remove(j)
while len(Q) > 0:
# 将第一个点赋值给q,Q队列输出给q,先入先出
q = Q[0]
Q.remove(q)
if len(neighbor_list[q]) >= min_Pts:
# &:按位与运算符,参与运算的两个值,如果两个相应位都为1,则该位的结果为1,
# 否则为0
delta = neighbor_list[q] & gama
deltalist = list(delta)
for i in range(len(delta)):
# 在Q中增加访问点
Q.append(deltalist[i])
# 从gama中移除访问点,剩余未访问点
gama = gama - delta
# 原始未访问点:剩余未访问点=访问点
Ck = gama_old - gama
Cklist = list(Ck)
for i in range(len(Ck)):
# 类型为k
cluster[Cklist[i]] = k
# 剩余核心点
omega_list = omega_list - Ck
return cluster
# 创建一个包含较小圆的大圆的样本集
X1, y1 = datasets.make_circles(n_samples=2000, factor=0.6, noise=0.02)
# 生成聚类算法的测试数据
X2, y2 = datasets.make_blobs(n_samples=400, n_features=2, centers=[[1.2, 1.2]], cluster_std=[[0.1]], random_state=9)
X = np.concatenate((X1, X2))
# 判断为邻域的半径
eps = 0.08
# 判断为核心点的样本数
min_Pts = 10
begin = time.time()
C = DBSCAN(X, eps, min_Pts)
end = time.time() - begin
plt.figure()
plt.scatter(X[:, 0], X[:, 1], c=C)
plt.show()
print(end)
print(X)
运行程序,输出如下,效果如下图所示:
54.39235258102417 [[-0.62951597 -0.04543715] [-0.22258548 0.56494867] [0.12975336 0.60202833] ... [1.3182636 1.23193706] [1.18114518 1.2700325] [1.06090269 1.20967997]]

图 2 DBSCAN聚类效果
利用 sklearn 中的 DBSCAN 类进行实现,代码为:
from sklearn.cluster import DBSCAN
import matplotlib.pyplot as plt
model = DBSCAN(eps=0.08, min_samples=10, metric='euclidean', algorithm='auto')
"""
eps:邻域半径
min_samples:对应minPts
metrics:邻域内距离计算方法,可选项如下.
欧氏距离:euclidean
曼哈顿距离:manhattan
切比雪夫距离:chebyshev
闵可夫斯基距离:minkowski
带权重的闵可夫斯基距离:wminkowski
标准化欧氏距离:seuclidean
马氏距离:mahalanobis
algorithm:最近邻搜索算法参数,算法一共有三种,
第一种是暴力实现brute,
第二种是KD树实现kd_tree,
第三种是球树实现ball_tree,
auto则会在上面三种算法中做权衡
"""
model.fit(X)
plt.figure()
plt.scatter(X[:, 0], X[:, 1], c=model.labels_)
plt.show()
得到效果与图 2 一致。 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: