K-means聚类算法详解
在非监督聚类算法中,最具代表性的是 K-means 算法,该算法的主要作用是将相似的样本自动归到一个类别中。
聚类的目的是将数据集中的样本划分为若干个不相交的子集,每个子集称为一个簇。聚类既能作为一个单独的过程,用于寻找数据内在的分布结构,也能作为分类等其他学习任务的预处理过程。
聚类是机器学习中新算法出现最多、最快的领域,一个重要的原因是聚类不存在客观标准,给定数据集总能从某个角度找到以往算法未覆盖的某种标准,从而设计出新算法。
K-means 算法十分简单易懂,而且非常有效,但是 K 值和 K 个初始聚类中心的确定对于聚类效果的好坏有很大的影响。众多研究者基于此提出了各自行之有效的解决方案,新的改进算法仍然不断被提出。
例如,要判定一个球是篮球、足球还是排球。解决这类问题的方法是先给出各种类型的球让算法学习,然后根据学习得到的经验对一个球的类型做出判定。这就像还没长大的小朋友,爸爸妈妈先拿各种道具球教他们,告诉他们每种球是什么样子的,接下来这些孩子就会认不同类型的球了。这种方法称为监督学习,它有训练和预测两个阶段,在训练阶段,用大量的样本进行学习,得到一个判定球类型的模型。
聚类的目标也是确定一个物体的类别,但和分类不同的是,这里没有事先定义好的类别,聚类算法要自己想办法把一批样本分成多个类,保证每一类中的样本是相似的,而不同类的样本是不同的。
以球的聚类为例,假设有一堆球,但事先没有说明有哪些类别,也没有一个训练好的判定类别的模型,聚类算法要自动将这堆球进行归类。这就相当于家长并没有事先告诉孩子们各种球是什么样子的,孩子们需要自己将球进行归类,而且这些球可能是他们不认识的。这里没有统一的、确定的划分标准,有些孩子将颜色相似的球归在了一起,而另一些孩子将大小相似的球归在了一起,还有一些孩子将纹理相似的球归在了一起。
聚类算法将一堆没有标签的数据自动划分成几类,并且保证同一类数据有相似的特征。
假设有四个牧师去郊区布道,一开始牧师们随意选了几个布道点,并且把这几个布道点的情况公告给了郊区所有的村民,于是每个村民到离自己家最近的布道点去听课。
听课之后,大家觉得距离太远了,于是每个牧师统计了一下自己的课上所有村民的地址,搬到了所有地址的中心地带,并且在海报上更新了自己的布道点的位置。牧师每一次移动不可能离所有人都更近,有的人发现 A 牧师移动以后自己去 B 牧师处听课更近,于是每个村民又去了离自己最近的布道点。
就这样,牧师每个礼拜更新自己的位置,村民根据自己的情况选择布道点,最终稳定了下来。可以看到,牧师的目的是使每个村民到其最近中心点的距离和最小。
与上述例子相似,K-means 算法的基本思想是,通过迭代寻找 K 个聚类的一种划分方案。其步骤是,先将数据分为 K 组,随机选择 K 个初始聚类中心(也可以随机选取 K 个对象作为初始聚类中心),然后计算每个对象与各个聚类中心之间的距离,把每个对象分配给距离它最近的聚类中心。
聚类中心以及分配给它的对象就代表一个聚类。每分配一个样本,聚类中心就会根据聚类中现有的对象被重新计算。这个过程将不断重复,直到满足某个终止条件。终止条件可以是没有(或最小数目)对象被重新分配给不同的聚类,或者没有(或最小数目)聚类中心再发生变化(或者发生的变化小于一定的阈值)。
经过上述分析,可以得到 K-means 算法进行聚类的步骤:

需要做的是将这些数据自动分为三个类别。待分类数据初始状态如下图所示。
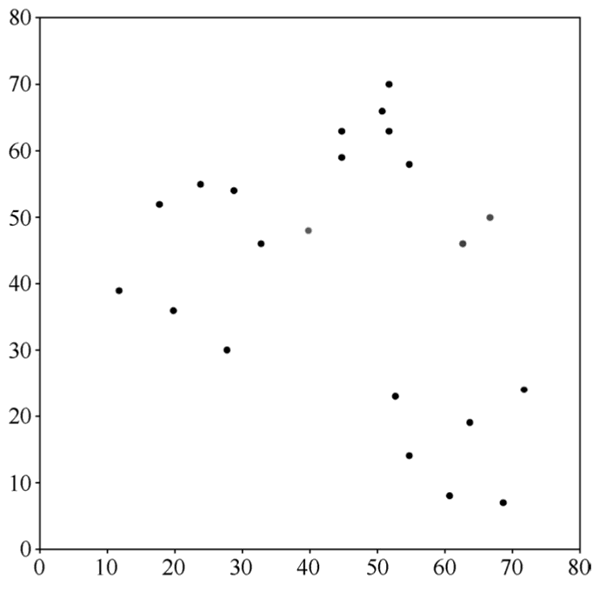
图 2 待分类数据初始状态
图 2 中每一个黑色的点代表一个待分类的数据。除此之外,还有一个红色的点、一个绿色的点和一个蓝色的点,这三个点是根据 K-means 算法随机生成的三个类的初始中心点,假设这三个类分别为 R 类、G 类和 B 类。
有了初始中心点之后,下一步就是计算黑色的数据点与每个类别的中心点之间的距离,按照就近划分的原则,对所有数据点进行自动分类,第一次自动分类结果如下图所示,有 2 个数据点离 R 类的中心点最近,所以划分为 R 类;有 11 个数据点离 G 类的中心点最近,所以划分为 G 类;有 6 个数据点离 B 类的中心点最近,所以划分为 B 类。
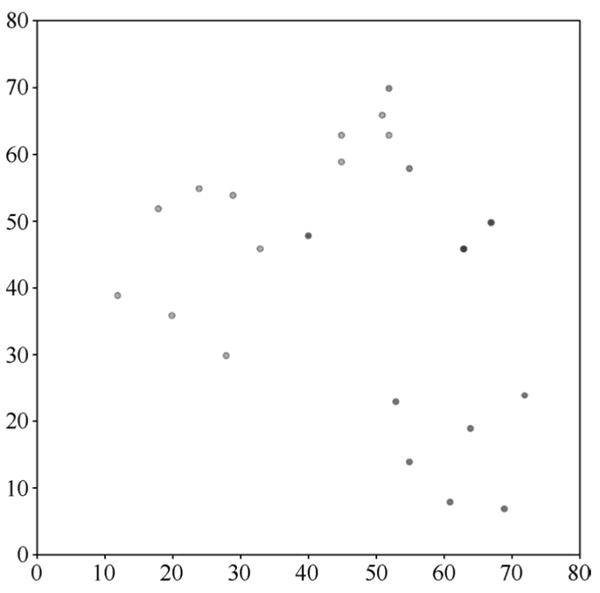
图 3 第一次自动分类结果
以第一次自动分类结果为依据,计算出每一个类别的新中心点,根据新的类别中心点,重新对每个数据点进行自动分类。

图 4 第二次自动分类结果
如上图中相应箭头所指向的数据点所示,箭头的长度表示类别中心点调整的幅度。在这一轮的调整中,由于之前属于 R 类的两个数据点离新的 G 类中心点比离新的 R 类中心点更近,所以由原来的 R 类重新划分到了 G 类。B 类的数据点没有发生任何变化,但是其类别中心点离所有的 B 类数据点更近了。
以第二次自动分类结果为依据,再一次计算出每一个类别的新中心点,根据新的类别中心点,重新对每个数据点进行自动分类。这一次分类之后,每个类别的数据点和第二次自动分类后的数据点完全一致,所以 K-means 算法执行结束,得到最终的分类结果,如下图所示。
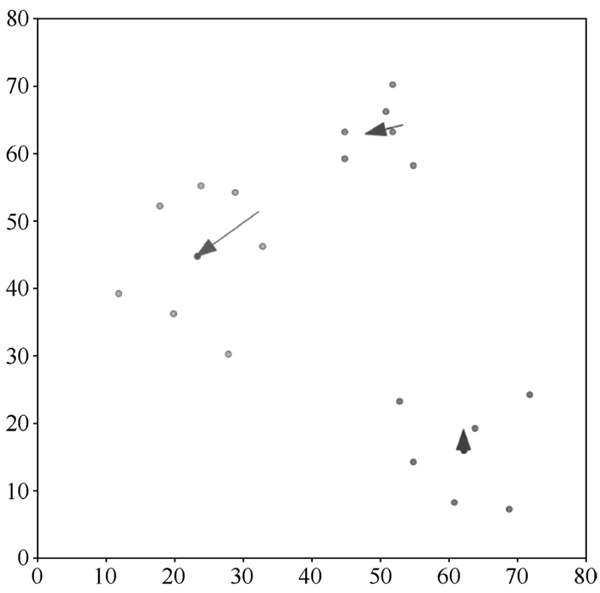
图 5 第三次自动分类结果
K-means 算法在具体应用的时候,每次执行会由于一些条件的设置不同而得到不一样的结果,其中比较重要的几个设置如下。
比如,一个游戏公司想把所有玩家分成顶级、高级、中级、初级四类,那么 K=4;一个房地产公司想把当地的商品房分成高、中、低三档,那么 K=3。
按需选择虽然合理,但未必能保证在执行 K-means 算法时能够得到清晰的分界线。
对于如下图所示的这种初始分布比较好的二维样本,可以比较清楚地看出初始 K 值应该为 3。

图 6 可以应用观察法的情况
这种方法虽然简单,但是要求原始数据维度低,一般是 2 维(平面散点)或者 3 维(立体散点),否则人类肉眼无法观察。对于高维数据,通常先利用 PCA 算法降维,再进行肉眼观察。
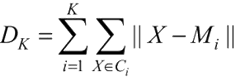
这里的距离可以采用欧氏距离。对于不同的 K,最后会得到不同的中心点和类别,所以会有不同的度量。
对上面的例子用不同的 K 去计算,会得到不同的结果。把 K 作为横坐标,DK 作为纵坐标,可以得到如下图所示的折线图。

图 8 手肘法折线图
很显然,K 越大,距离和越小。但是注意到 K=3 是一个拐点,就像人的肘部一样,K=3 之前下降很快,K=3 之后趋于平稳。手肘法认为这个拐点就是最佳的 K。
手肘法是一种经验方法,其效果因人而异,特别是遇到模棱两可的情况时。相比于直接观察法,手肘法的一个优点是适用于高维的样本数据。
这种方法对经验的依赖度很高,如果经验丰富,那么得到的结果可能比较好;如果经验不够,那么得到的结果可能会很糟。
在计算了全部样本点的密度后,选择密度最大的样本点作为第 1 个分类中心。它对应样本分布的一个最高的峰值点。在选择第 2 个分类中心时,可以人为规定一个数 r>0,在离开第 1 个代表点距离 r 以外选择次大的密度点作为第 2 个分类中心,其余代表点的选择与此类似。这样就可以避免分类中心集中在一起的问题。
这种方法的劣势是初始计算量比较大。
这种压缩方法的本质是量化矢量(Vector Quaintization),通过 K-means 聚类得到量化表,将每个像素用量化表中的矢量来表示,然后记录每个像素对应的索引值,这样原来使用 24bit 来表示一个像素,现在只需要存储记录索引值所需要的 bit 数就可以了,因此实现了图像压缩。

图 9 K-means图像压缩
上图所示的分辨率分别是 128×128 像素的三通道原图,以及颜色数目压缩为 2 个、4 个、8 个、16 个、32 个、64 个和 128 个的效果。
可以看到,当保存的颜色数目太少时,画质会有明显的降低,甚至无法识别出其中的物体(比如颜色数目为 2 个的时候),但是当保留的颜色数目逐渐增加到 128 个的时候,虽然信息损失了 50%(原始的颜色数目为 256 个),但是对画质的影响没有想象的大。
聚类的目的是将数据集中的样本划分为若干个不相交的子集,每个子集称为一个簇。聚类既能作为一个单独的过程,用于寻找数据内在的分布结构,也能作为分类等其他学习任务的预处理过程。
聚类是机器学习中新算法出现最多、最快的领域,一个重要的原因是聚类不存在客观标准,给定数据集总能从某个角度找到以往算法未覆盖的某种标准,从而设计出新算法。
K-means 算法十分简单易懂,而且非常有效,但是 K 值和 K 个初始聚类中心的确定对于聚类效果的好坏有很大的影响。众多研究者基于此提出了各自行之有效的解决方案,新的改进算法仍然不断被提出。
什么是聚类
分类问题是机器学习中最常见的一类问题,它的目标是确定一个物体所属的类别。例如,要判定一个球是篮球、足球还是排球。解决这类问题的方法是先给出各种类型的球让算法学习,然后根据学习得到的经验对一个球的类型做出判定。这就像还没长大的小朋友,爸爸妈妈先拿各种道具球教他们,告诉他们每种球是什么样子的,接下来这些孩子就会认不同类型的球了。这种方法称为监督学习,它有训练和预测两个阶段,在训练阶段,用大量的样本进行学习,得到一个判定球类型的模型。
聚类的目标也是确定一个物体的类别,但和分类不同的是,这里没有事先定义好的类别,聚类算法要自己想办法把一批样本分成多个类,保证每一类中的样本是相似的,而不同类的样本是不同的。
以球的聚类为例,假设有一堆球,但事先没有说明有哪些类别,也没有一个训练好的判定类别的模型,聚类算法要自动将这堆球进行归类。这就相当于家长并没有事先告诉孩子们各种球是什么样子的,孩子们需要自己将球进行归类,而且这些球可能是他们不认识的。这里没有统一的、确定的划分标准,有些孩子将颜色相似的球归在了一起,而另一些孩子将大小相似的球归在了一起,还有一些孩子将纹理相似的球归在了一起。
聚类算法将一堆没有标签的数据自动划分成几类,并且保证同一类数据有相似的特征。
K-means算法介绍
这里可以用一个例子来说明 K-means 算法的大致过程,即著名的牧师—村民模型。假设有四个牧师去郊区布道,一开始牧师们随意选了几个布道点,并且把这几个布道点的情况公告给了郊区所有的村民,于是每个村民到离自己家最近的布道点去听课。
听课之后,大家觉得距离太远了,于是每个牧师统计了一下自己的课上所有村民的地址,搬到了所有地址的中心地带,并且在海报上更新了自己的布道点的位置。牧师每一次移动不可能离所有人都更近,有的人发现 A 牧师移动以后自己去 B 牧师处听课更近,于是每个村民又去了离自己最近的布道点。
就这样,牧师每个礼拜更新自己的位置,村民根据自己的情况选择布道点,最终稳定了下来。可以看到,牧师的目的是使每个村民到其最近中心点的距离和最小。
与上述例子相似,K-means 算法的基本思想是,通过迭代寻找 K 个聚类的一种划分方案。其步骤是,先将数据分为 K 组,随机选择 K 个初始聚类中心(也可以随机选取 K 个对象作为初始聚类中心),然后计算每个对象与各个聚类中心之间的距离,把每个对象分配给距离它最近的聚类中心。
聚类中心以及分配给它的对象就代表一个聚类。每分配一个样本,聚类中心就会根据聚类中现有的对象被重新计算。这个过程将不断重复,直到满足某个终止条件。终止条件可以是没有(或最小数目)对象被重新分配给不同的聚类,或者没有(或最小数目)聚类中心再发生变化(或者发生的变化小于一定的阈值)。
经过上述分析,可以得到 K-means 算法进行聚类的步骤:
- 从数据中确定 K 个初始聚类中心。
- 计算每个聚类对象到聚类中心的距离,按照就近划分的原则将每个聚类对象划分到对应的类别。
- 根据重新聚类之后的结果,再次计算每个聚类中心。
- 判断是否满足停止迭代的条件,如果已经满足,则停止迭代;否则继续操作,直到达到最大迭代次数。
K-means算法求解步骤
现在假设有如下所示的一批二维坐标数据:
需要做的是将这些数据自动分为三个类别。待分类数据初始状态如下图所示。

图 2 待分类数据初始状态
图 2 中每一个黑色的点代表一个待分类的数据。除此之外,还有一个红色的点、一个绿色的点和一个蓝色的点,这三个点是根据 K-means 算法随机生成的三个类的初始中心点,假设这三个类分别为 R 类、G 类和 B 类。
有了初始中心点之后,下一步就是计算黑色的数据点与每个类别的中心点之间的距离,按照就近划分的原则,对所有数据点进行自动分类,第一次自动分类结果如下图所示,有 2 个数据点离 R 类的中心点最近,所以划分为 R 类;有 11 个数据点离 G 类的中心点最近,所以划分为 G 类;有 6 个数据点离 B 类的中心点最近,所以划分为 B 类。

图 3 第一次自动分类结果
以第一次自动分类结果为依据,计算出每一个类别的新中心点,根据新的类别中心点,重新对每个数据点进行自动分类。

图 4 第二次自动分类结果
如上图中相应箭头所指向的数据点所示,箭头的长度表示类别中心点调整的幅度。在这一轮的调整中,由于之前属于 R 类的两个数据点离新的 G 类中心点比离新的 R 类中心点更近,所以由原来的 R 类重新划分到了 G 类。B 类的数据点没有发生任何变化,但是其类别中心点离所有的 B 类数据点更近了。
以第二次自动分类结果为依据,再一次计算出每一个类别的新中心点,根据新的类别中心点,重新对每个数据点进行自动分类。这一次分类之后,每个类别的数据点和第二次自动分类后的数据点完全一致,所以 K-means 算法执行结束,得到最终的分类结果,如下图所示。

图 5 第三次自动分类结果
K-means 算法在具体应用的时候,每次执行会由于一些条件的设置不同而得到不一样的结果,其中比较重要的几个设置如下。
1、K值的确定
对于 K 值的确定,通常有以下几种方法。1) 按需选择
简单地说就是按照建模的需求和目的来选择 K 值。比如,一个游戏公司想把所有玩家分成顶级、高级、中级、初级四类,那么 K=4;一个房地产公司想把当地的商品房分成高、中、低三档,那么 K=3。
按需选择虽然合理,但未必能保证在执行 K-means 算法时能够得到清晰的分界线。
2) 观察法
观察法就是用肉眼观察,看所有数据点大概聚成几堆。对于如下图所示的这种初始分布比较好的二维样本,可以比较清楚地看出初始 K 值应该为 3。

图 6 可以应用观察法的情况
这种方法虽然简单,但是要求原始数据维度低,一般是 2 维(平面散点)或者 3 维(立体散点),否则人类肉眼无法观察。对于高维数据,通常先利用 PCA 算法降维,再进行肉眼观察。
3) 手肘法
手肘法本质上是一种间接的观察法。这里需要介绍一些背景知识。当 K-means 算法完成后,将得到 K 个类别的中心点 Mi,i=1,2,…,K,以及每个原始点所对应的类别 Ci,i=1,2,…,K。通常采用所有样本点到它所在的类别的中心点的距离和作为模型的度量,记为 DK。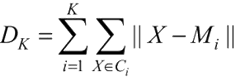
这里的距离可以采用欧氏距离。对于不同的 K,最后会得到不同的中心点和类别,所以会有不同的度量。
对上面的例子用不同的 K 去计算,会得到不同的结果。把 K 作为横坐标,DK 作为纵坐标,可以得到如下图所示的折线图。

图 8 手肘法折线图
很显然,K 越大,距离和越小。但是注意到 K=3 是一个拐点,就像人的肘部一样,K=3 之前下降很快,K=3 之后趋于平稳。手肘法认为这个拐点就是最佳的 K。
手肘法是一种经验方法,其效果因人而异,特别是遇到模棱两可的情况时。相比于直接观察法,手肘法的一个优点是适用于高维的样本数据。
2、初始的K个类别中心的确定
对于初始的 K 个类别中心的确定,通常有以下几种方法。1) 凭经验选择
这种方法是根据问题的性质,依据经验从数据点中找出从直观上看来比较合适的代表点。这种方法对经验的依赖度很高,如果经验丰富,那么得到的结果可能比较好;如果经验不够,那么得到的结果可能会很糟。
2) 随机选择 K 个样本点作为 K 个类别的中心
这种方法对随机选择的K个样本点是否符合真实数据类别中心的分布要求比较高,所以是一种结果不太可控的方法。3) 将全部数据随机分成 K 类,计算每类的重心,将这些重心作为每类的代表点
这种方法和第 2 种方法类似,只是其计算得到的 K 个类别中心,相对来说出现较大偏差的可能性稍小一点。4) 用密度法选择初始分类中心
这里的密度是指具有统计性质的样本密度。一种求法是,以每个样本点为球心,用某个正数 r 为半径确定一个球形区域,落在该球内的样本点数就是该点的密度。在计算了全部样本点的密度后,选择密度最大的样本点作为第 1 个分类中心。它对应样本分布的一个最高的峰值点。在选择第 2 个分类中心时,可以人为规定一个数 r>0,在离开第 1 个代表点距离 r 以外选择次大的密度点作为第 2 个分类中心,其余代表点的选择与此类似。这样就可以避免分类中心集中在一起的问题。
这种方法的劣势是初始计算量比较大。
K-means算法实例
图像的每一个点的像素值都可以视作一个三维向量(RGB 三通道图像),那么,使用 K-means 算法对这些点进行聚类,就很容易得到几个中心点和几类,把同一类的数据点(像素点)用中心点表示就可以得到压缩后的图像。这种压缩方法的本质是量化矢量(Vector Quaintization),通过 K-means 聚类得到量化表,将每个像素用量化表中的矢量来表示,然后记录每个像素对应的索引值,这样原来使用 24bit 来表示一个像素,现在只需要存储记录索引值所需要的 bit 数就可以了,因此实现了图像压缩。

图 9 K-means图像压缩
上图所示的分辨率分别是 128×128 像素的三通道原图,以及颜色数目压缩为 2 个、4 个、8 个、16 个、32 个、64 个和 128 个的效果。
可以看到,当保存的颜色数目太少时,画质会有明显的降低,甚至无法识别出其中的物体(比如颜色数目为 2 个的时候),但是当保留的颜色数目逐渐增加到 128 个的时候,虽然信息损失了 50%(原始的颜色数目为 256 个),但是对画质的影响没有想象的大。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: