Python K-means聚类算法详解(附带实例)
聚类类似于分类,不同的是,聚类所划分的类是未知的,也就是说不知道数据应该属于哪类,需要通过一定的算法自动分类。
在实际应用中,聚类是一个将在某些方面相似的数据进行分类汇总的过程(简单地说就是将相似的数据聚在一起),如图 1 和图 2 所示。

图 1 聚类前
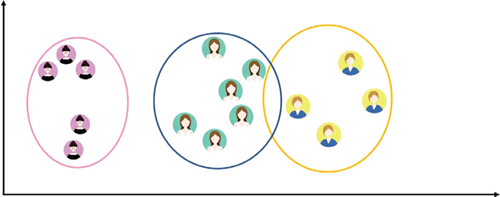
图 2 聚类后
聚类分析主要的应用领域如下:
k-means 算法是一种聚类算法,它是一种无监督学习算法,目的是将相似的对象归到同一个簇中。簇内的对象越相似,聚类的效果就越好。
传统的聚类算法包括划分方法、层次方法、基于密度方法、基于网格方法和基于模型方法。本节主要介绍 k-means 聚类算法,它是划分方法中较典型的一种,也被称为 k 均值聚类算法。
给定一个数据集合和需要的聚类数目 k,k 由用户指定,k-means 聚类算法将根据某个距离函数反复把数据分入 k 个聚类中。
这个过程将不断重复直到满足某个终止条件。终止条件可以是以下的任何一个:
伪代码如下:
首先导入 sklearn.cluster 模块的 KMeans() 方法,程序代码如下:
接下来就可以在程序中使用 KMeans() 方法了。KMeans() 方法的语法格式如下:
主要属性:
主要方法:
【实例】对一组数据聚类。
Scikit-Learn的make_blobs() 方法用于生成聚类算法的测试数据,直观地说,make_blobs() 方法可以根据用户指定的特征数量、质心数量、范围等生成几类数据,这些数据可用于测试聚类算法的效果。
make_blobs() 方法的语法格式如下:
【实例】生成用于聚类的测试数据(500 个样本,每个样本有两个特征),程序代码如下:
接下来,通过 KMeans() 方法对测试数据进行聚类,程序代码如下:
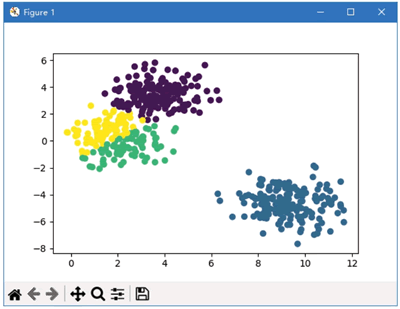
图 3 聚类散点图
从分析结果得知,相似的数据聚在一起,分成了 4 堆,也就是 4 类,并以不同的颜色显示,看上去清晰直观。
在实际应用中,聚类是一个将在某些方面相似的数据进行分类汇总的过程(简单地说就是将相似的数据聚在一起),如图 1 和图 2 所示。

图 1 聚类前

图 2 聚类后
聚类分析主要的应用领域如下:
- 商业:聚类分析被用来发现不同的客户群,并且通过购买模式刻画不同客户群的特征;
- 生物学:聚类分析被用来对动植物和对基因进行分类,获取对种群固有结构的认识;
- 保险行业:聚类分析通过一个高的平均消费来鉴定汽车保险单持有者的分类,同时根据住宅类型、价值和地理位置来判断一个城市的房产分类;
- 因特网:聚类分析被用来在网上进行文档归类;
- 电子商务:聚类分析在电子商务网站建设和数据挖掘中应用广泛,通过分组聚类获取有相似浏览行为的客户,并分析客户的共同特征,更好地帮助商家了解自己的客户,以便向客户提供更合适的服务。
k-means 算法是一种聚类算法,它是一种无监督学习算法,目的是将相似的对象归到同一个簇中。簇内的对象越相似,聚类的效果就越好。
传统的聚类算法包括划分方法、层次方法、基于密度方法、基于网格方法和基于模型方法。本节主要介绍 k-means 聚类算法,它是划分方法中较典型的一种,也被称为 k 均值聚类算法。
K-means聚类概述
k-means 聚类也称 k 均值聚类,是著名的聚类算法,由于简洁和高效,它成为所有聚类算法中应用最为广泛的一种。给定一个数据集合和需要的聚类数目 k,k 由用户指定,k-means 聚类算法将根据某个距离函数反复把数据分入 k 个聚类中。
K-means聚类算法原理
随机选取 k 个数据作为初始质心(质心即簇中所有数据的中心),然后将集中的数据分配到一个簇中,具体来说,就是为每个数据找到距其最近的质心,并将其分配给该质心所对应的簇。这一步完成之后,每个簇的质心更新为该簇所有数据的平均值。这个过程将不断重复直到满足某个终止条件。终止条件可以是以下的任何一个:
- 没有(或最小数目)对象被重新分配给不同的簇;
- 没有(或最小数目)簇中心发生变化;
- 误差平方和达到局部最小。
伪代码如下:
创建 k 个点作为起始质心,可以随机选择(位于数据边界内)
当任意一个点的簇分配结果发生改变时,初始化为 True
对数据集中每个数据,重新分配质心
对每个质心
计算质心与数据之间的距离
将数据分配到距其最近的簇
对每一个簇,计算簇中所有数据的平均值并将该值作为新的质心
通过以上介绍,相信你对 k-means 聚类算法已经有了初步的认识。在 Python 中应用该算法无须手动编写代码,因为 Python 第三方模块 Scikit-Learn 已经帮我们写好了,在性能和稳定性上比自己编写好得多,只需在程序中调用即可。 Python聚类模块
Scikit-Learn 的 cluster 模块用于聚类分析,该模块提供了很多聚类算法,下面主要介绍 KMeans() 方法,该方法通过 k-means 聚类算法实现聚类分析。首先导入 sklearn.cluster 模块的 KMeans() 方法,程序代码如下:
from sklearn.cluster import KMeans
接下来就可以在程序中使用 KMeans() 方法了。KMeans() 方法的语法格式如下:
sklearn.cluster.KMeans(
n_clusters=8,
*,
init='k-means++',
n_init='warn',
max_iter=300,
tol=0.0001,
verbose=0,
random_state=None,
copy_x=True,
algorithm='lloyd'
)
参数说明:| 参数名 | 说明 |
|---|---|
| n_clusters | 整型,默认值为 8,生成的聚类数,即质心(centroids)数。 |
| init |
取值 k-means++(默认)、random 或 shape=(n_clusters, n_features) 的数组向量。
|
| n_init | 整型,默认 10,用不同初始质心运行算法的次数。 |
| max_iter | 整型,默认 300,单次 k-means 的最大迭代次数。 |
| tol | 浮点型,默认 0.0001,控制求解精度。 |
| verbose | 整型,默认 0,冗长模式开关。 |
| random_state | 整型或随机数生成器,设置随机种子。默认使用 NumPy 的随机数生成器。 |
| copy_x |
布尔值,默认 True。 True:不修改原始数据。 False:直接在原始数据上操作,可能产生细微差异。 |
| algorithm | 算法实现方式,取值为 lloyd(默认)、elkan、auto、full。 |
主要属性:
- cluster_centers_:返回数组,表示分类簇的均值向量;
- labels_:返回数组,表示每个样本数据所属的类别标记;
- inertia_:返回数组,表示每个样本数据与它们各自质心的距离之和。
主要方法:
- fit(X[, y]):计算 k-means 聚类;
- fit_predictt(X[, y]):计算簇质心并为每个样本数据预测类别;
- predict(X):为每个样本数据估计最近的簇;
- score(X[, y]):计算聚类误差。
【实例】对一组数据聚类。
import numpy as np
from sklearn.cluster import KMeans
X = np.array([[1,10],[1,11],[1,12],[3,20],[3,23],[3,21],[3,25]])
kmodel = KMeans(n_clusters=2, n_init='auto') # 调用 KMeans 方法实现聚类(两类)
y_pred = kmodel.fit_predict(X) # 预测类别
print("预测类别:", y_pred)
print("聚类中心坐标值:\n", kmodel.cluster_centers_)
print("类别标记:", kmodel.labels_)
运行程序,结果如下:
预测类别:[0 0 0 1 1 1 1]
聚类中心坐标值:
[[ 1. 11. ]
[ 3. 22.25]]
类别标记:[0 0 0 1 1 1 1]
聚类数据生成器
前面举了一个简单的聚类示例,但是聚类效果并不明显。接下面生成专门的聚类算法测试数据,可以更好地诠释聚类算法,展示聚类效果。Scikit-Learn的make_blobs() 方法用于生成聚类算法的测试数据,直观地说,make_blobs() 方法可以根据用户指定的特征数量、质心数量、范围等生成几类数据,这些数据可用于测试聚类算法的效果。
make_blobs() 方法的语法格式如下:
sklearn.datasets.make_blobs(
n_samples=100,
n_features=2,
centers=3,
cluster_std=1.0,
center_box=(-10.0, 10.0),
shuffle=True,
random_state=None
)
主要参数说明:
- n_samples:待生成的样本总数;
- n_features:每个样本的特征数;
- centers:类别数;
- cluster_std:每个类别的方差,例如,生成两类数据,其中一类比另一类具有更大的方差,可以将 cluster_std 设置为 [1.0, 3.0]。
【实例】生成用于聚类的测试数据(500 个样本,每个样本有两个特征),程序代码如下:
from sklearn.datasets import make_blobs from matplotlib import pyplot as plt X, y = make_blobs(n_samples=500, n_features=2, centers=3)
接下来,通过 KMeans() 方法对测试数据进行聚类,程序代码如下:
from sklearn.cluster import KMeans y_pred = KMeans(n_clusters=4, random_state=9, n_init='auto').fit_predict(X) plt.scatter(X[:, 0], X[:, 1], c=y_pred) plt.show()运行程序,结果如下图所示:

图 3 聚类散点图
从分析结果得知,相似的数据聚在一起,分成了 4 堆,也就是 4 类,并以不同的颜色显示,看上去清晰直观。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: