kNN算法(k邻近算法)详解(附带实例,Python实现)
监督学习要解决的问题可分成两类:回归(regression)和分类(classification)。监督学习的算法有很多,而且很多算法已经被收集到成熟的算法库中,使用者可以直接调用,其中 k邻近(k-nearest neighbor,kNN)算法就是常用的经典算法之一。
kNN 算法采用测量不同特征值之间的距离方法进行分类,即是给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的 k 个实例,这 k 个实例的多数属于某个类,就把该输入实例分类到这个类中。
kNN 算法是一种监督学习算法,其基本操作的三个要点如下:
kNN 算法不具有显式的学习过程。它是懒惰学习(lazy learning)的著名代表,此类学习技术在训练阶段仅仅是把样本保存起来,训练时间开销为零,待收到测试样本后再进行处理。
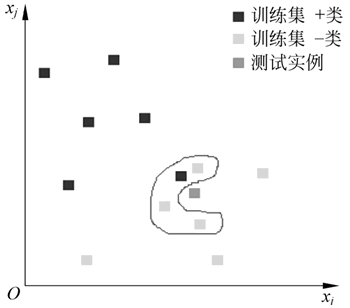
图 1 分类决策效果
如图 1 所示,根据欧氏距离,选择 k=4 个离测试实例最近的训练实例(圈处),再根据多数表决的分类决策规则,即这 4 个实例多数属于“-类”,可推断测试实例为“-类”。
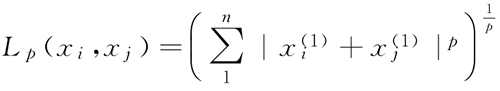
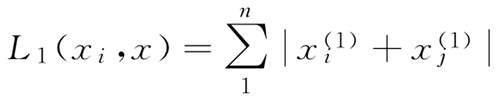
当 p=2 时,称为欧氏距离(Euclidean distance):

当 p=∞ 时,它是各个坐标距离的最大值,如下图所示:

图 5 距离的最大值
注意:
说明:
【实例】利用 kNN 算法分析鸢尾花的数据集。
kNN 算法采用测量不同特征值之间的距离方法进行分类,即是给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的 k 个实例,这 k 个实例的多数属于某个类,就把该输入实例分类到这个类中。
kNN 算法是一种监督学习算法,其基本操作的三个要点如下:
- 第一,确定距离度量;
- 第二,k 值的选择(找出训练集中与带估计点最靠近的 k 个实例点);
-
第三,分类决策规则:
- 在“分类”任务中可使用“投票法”,即选择这个实例中出现最多的标记类别作为预测结果;
- 在“回归”任务中可使用“平均法”,即将这 k 个实例的实值输出标记的平均值作为预测结果;
- 还可基于距离远近进行加权平均或加权投票,距离越近的实例权重越大。
kNN 算法不具有显式的学习过程。它是懒惰学习(lazy learning)的著名代表,此类学习技术在训练阶段仅仅是把样本保存起来,训练时间开销为零,待收到测试样本后再进行处理。
kNN算法的三要素
距离度量、k 值的选择及分类决策规则是 kNN 算法的三个基本要素。
图 1 分类决策效果
如图 1 所示,根据欧氏距离,选择 k=4 个离测试实例最近的训练实例(圈处),再根据多数表决的分类决策规则,即这 4 个实例多数属于“-类”,可推断测试实例为“-类”。
1) 距离度量
特征空间中的两个实例点的距离是两个实例点相似程度的反映。kNN 算法的特征空间一般是 n维实数向量空间 Rn。度量的距离是其他 Lp 范式距离,一般为欧式距离。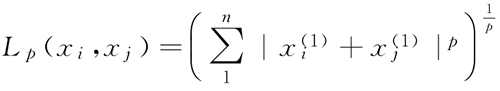
当 p=1 时,称为曼哈顿距离(Manhattan distance):式中,p≥1。
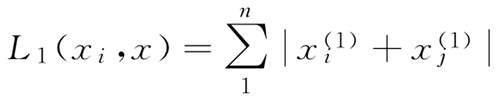
当 p=2 时,称为欧氏距离(Euclidean distance):

当 p=∞ 时,它是各个坐标距离的最大值,如下图所示:

图 5 距离的最大值
2) k值的选择
k 值的选择常用的方法有:- 从 k=1 开始,使用检验集估计分类器的误差率;
- 重复该过程,每次 k 增值 1,允许增加一个近邻;
- 选取产生最小误差率的 k。
注意:
- 一般 k 的取值不超过 20,上限是 n 的开方,随着数据集的增大,k 的值也要增大。
- 一般 k 值选取比较小的数值,并采用交叉验证法选择最优的 k 值。
说明:
- 过小的 k 值模型中,输入样本点会对近邻的训练样本点十分敏感,如果引入了噪声,则会导致预测出错。对噪声的低容忍性会使得模型变得过拟合;
- 过大的 k 值模型中,就相当于选择了范围更大的领域内的点作为决策依据,可以降低估计误差。但邻域内其他类别的样本点也会对该输入样本点的预测产生影响;
- 如果 k=N,N 为所有样本点,那么 kNN 算法模型每次都将会选取训练数据中数量最多的类别作为预测类别,训练数据中的信息将不会被利用。
3) 分类决策规则
kNN 的分类决策规则就是对输入新样本的邻域内所有样本进行统计数目。邻域的定义就是,以新输入样本点为中心,离新样本点距离最近的 k 个点所构成的区域。kNN算法实现
前面已对 kNN 算法的定义、三要素等进行了介绍,下面直接通过实例演示利用 Python 实现 kNN 算法。【实例】利用 kNN 算法分析鸢尾花的数据集。
from sklearn import datasets
#导入内置数据集模块
from sklearn.neighbors import KNeighborsClassifier
#导入sklearn.neighbors模块中kNN类
import numpy as np
iris = datasets.load_iris()
#print(iris)
#导入鸢尾花的数据集,iris是一个数据集,内部有样本数据
iris_x = iris.data
iris_y = iris.target
indices = np.random.permutation(len(iris_x))
#permutation接收一个数作为参数(150),产生一个0~149一维数组,只不过是随机打乱的
iris_x_train = iris_x[indices[:-10]]
#随机选取140个样本作为训练数据集
iris_y_train = iris_y[indices[:-10]]
#并且选取这140个样本的标签作为训练数据集的标签
iris_x_test = iris_x[indices[-10:]]
#剩下的10个样本作为测试数据集
iris_y_test = iris_y[indices[-10:]]
#并且把剩下10个样本对应标签作为测试数据集的标签
knn = KNeighborsClassifier()
#定义一个kNN分类器对象
knn.fit(iris_x_train,iris_y_train)
#调用该对象的训练方法,主要接收两个参数:训练数据集及其样本标签
iris_y_predict = knn.predict(iris_x_test)
#调用该对象的测试方法,主要接收一个参数:测试数据集
score = knn.score(iris_x_test,iris_y_test,sample_weight = None)
#调用该对象的打分方法,计算出准确率
print('测试的结果 = ')
print(iris_y_predict)
#输出测试的结果
print('原始测试数据集的正确标签 = ')
print(iris_y_test)
#输出原始测试数据集的正确标签,以方便对比
print('准确率计算结果:',score)
#输出准确率计算结果
运行程序,输出如下:
测试的结果 =
[0 0 2 2 2 2 0 0 0 0]
原始测试数据集的正确标签 =
[0 0 2 1 2 2 0 0 0 0]
准确率计算结果:0.9
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: