Python KNN算法的具体实现(附带实例)
K 近邻算法(KNN)是一种简单但也很常用的分类算法,它也可以应用于回归计算。
KNN 是无参数学习,这意味着它不会对底层数据的分布做出任何假设。它是基于实例,即该算法没有显式的学习模型。相反,它选择的是记忆训练实例,并在一个有监督的学习环境中使用。
KNN 算法的实现过程主要包括距离计算方式的选择、k 值的选取以及分类的决策规则三部分。
给定训练集:Xtrain=(x(1), x(2), …, x(i)),测试集:Xtest=(x'(1), x'(2), …, x'(j))。则欧几里得距离为:
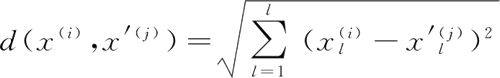
曼哈顿距离为:
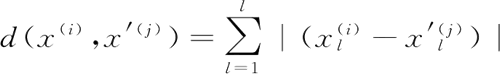
一般会先选择较小的 k 值,然后进行交叉验证选取最优的 k 值。k 值较小时,整体模型会变得复杂,且对近邻的训练数据点较为敏感,容易出现过拟合。k 值较大时,模型则会趋于简单,此时较远的训练数据点也会起到预测作用,容易出现欠拟合。
【实例】 KNN 算法预测数据。
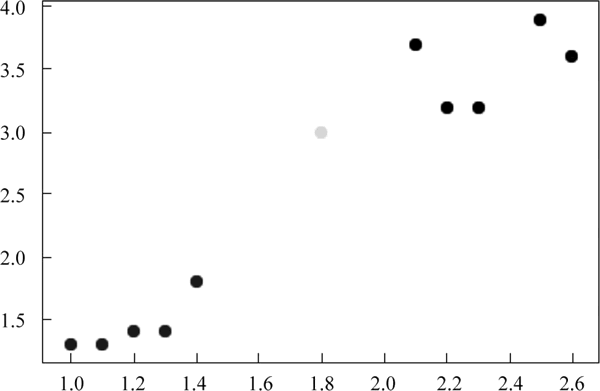
图 1 KNN 分类效果
KNN 是无参数学习,这意味着它不会对底层数据的分布做出任何假设。它是基于实例,即该算法没有显式的学习模型。相反,它选择的是记忆训练实例,并在一个有监督的学习环境中使用。
KNN 算法的实现过程主要包括距离计算方式的选择、k 值的选取以及分类的决策规则三部分。
KNN距离计算方式的选择
选择一种距离计算方式,计算测试数据与各个训练数据之间的距离。距离计算方式一般选择欧氏距离或曼哈顿距离。给定训练集:Xtrain=(x(1), x(2), …, x(i)),测试集:Xtest=(x'(1), x'(2), …, x'(j))。则欧几里得距离为:
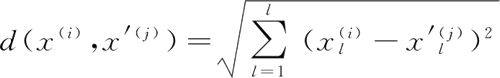
曼哈顿距离为:
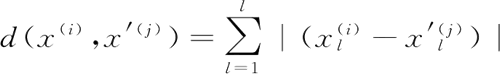
k值的选取
在计算测试数据与各个训练数据之间的距离之后,首先按照距离递增次序进行排序,然后选取距离最小的k个点。一般会先选择较小的 k 值,然后进行交叉验证选取最优的 k 值。k 值较小时,整体模型会变得复杂,且对近邻的训练数据点较为敏感,容易出现过拟合。k 值较大时,模型则会趋于简单,此时较远的训练数据点也会起到预测作用,容易出现欠拟合。
分类的决策规则
常用的分类决策规则是取 k 个近邻训练数据中类别出现次数最多者作为输入新实例的类别。即首先确定前 k 个点所在类别的出现频率,对于离散分类,返回前 k 个点出现频率最多的类别作预测分类;对于回归则返回前 k 个点的加权值作为预测值。【实例】 KNN 算法预测数据。
import numpy as np
import matplotlib.pyplot as plt
from math import sqrt
from collections import Counter # 统计工具包,待会用来统计最短距离最多的点的个数
x = [[1.0,1.3],[1.1,1.3],[1.2,1.4],[1.3,1.4],[1.4,1.8],[2.3,3.2],
[2.1,3.7],[2.2,3.2],[2.5,3.9],[2.6,3.6]]
# x 中的每一个元素代表,图上的每一个点
# y 列表里只有 0,1 两个数,代表 x 里的点分为两类,y 里面 0 的个数代表 x 里面点是"0"这一类的个数
y = [0,0,0,0,0,1,1,1,1,1]
X = np.array(x)
Y = np.array(y)
# 将列表转换为数组,这样做是为了便于用函数求最大、最小、排序、均值等的计算
plt.scatter(X[Y==0,0],X[Y==0,1],c='red')
plt.scatter(X[Y==1,0],X[Y==1,1],c='blue') # 将数据点可视化
newdata = [1.8,3.0] # 这是我要测试的数据点
plt.scatter(newdata[0],newdata[1],c='yellow')
# 步骤一:为了求数据点到我每一个测试点的距离,用欧氏距离格式求
dis = []
for i in X:
d = sqrt(np.sum((i - newdata)**2))
dis.append(d)
# 步骤二:使用该函数,让距离从小到大排序,注意这里排的是索引值
near = np.argsort(dis)
# 步骤三:设 k 值为 3,则取最小距离前三个的类别,哪个类别个数多,就把新数据判给哪个类
k = 3
# 步骤四:确定前 k 个点所在类别的出现频率
topk = [Y[i] for i in near[:3]]
print(topk) # 输出最短距离的前三个点都是什么类别
v = Counter(topk) # 统计 topk 里,即最短的三个点里,它们所属类别的个数
# 步骤五:最后确定要判别的点的类别
v.most_common(1) # 表现出最频繁出现的类别
v = v.most_common(1)[0][0] # 得出了 newdata 的类别了
print(v)
plt.show()
运行程序,输出如下:
[1,1,1]
Counter({1:3})
1

图 1 KNN 分类效果
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: