半监督学习详解(附带实例,Python实现)
半监督学习(semi-supervised learning, SSL)是模式识别和机器学习领域研究的重点问题,是监督学习与无监督学习相结合的一种学习方法。
当使用半监督学习时,将会要求尽量少的人员来从事工作,同时,又能够带来比较高的准确性,因此,半监督学习正越来越受到人们的重视。
半监督学习的有效性通常基于如下假设:
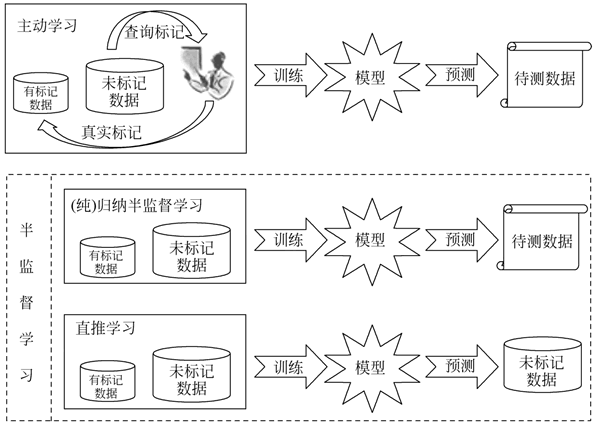
图 1 半监督学习流程图
假设每个样本可以从不同的角度训练出不同的分类器,然后用这些从不同角度训练出来的分类器对无标签样本进行分类,再选出认为可信的无标签样本加入训练集中。
生成式方法可以直接关注半监督学习和决策中的条件概率问题,避免对边缘概率或联合概率的建模以及求解,然而该方法对一些假设条件比较苛刻,一旦假设的 p(x|yi) 与样本数据的实际分布情况差距比较大,其分类效果往往不佳。
标签传播算法(LPA)是基于图的半监督学习算法,基本思路是从已标记的节点标签信息来预测未标记的节点标签信息。
【实例】用半监督学习做数字识别。假设有一份数据集,共 330 个数字,其中前十个是已知的,已经标注好了,后 320 个未知的,需要预测出来。步骤如下:
可以通过改变参数 max_iterations 将这个值增加到 30 以上。

图 2 半监督实现数字识别
当使用半监督学习时,将会要求尽量少的人员来从事工作,同时,又能够带来比较高的准确性,因此,半监督学习正越来越受到人们的重视。
半监督思想
半监督思想是在标记样本数量较少的情况下,通过在模型训练中直接引入无标记样本,充分捕捉数据整体潜在分布,以改善如传统无监督学习过程盲目性、监督学习在训练样本不足导致的学习效果不佳等问题。半监督学习的有效性通常基于如下假设:
- 平滑假设:稠密数据区域的两个距离很近的样例的类标签相似;
- 聚类假设:当两个样例位于同一聚类簇时,具有相同类标签的概率很大;
- 流形假设:高维数据嵌入低维流形中,当两个样例位于低维流形中的一个小局部邻域内时,具有相似的类标签。当模型假设不正确时,无标签的样本可能无法有效地提供增益信息,反而会恶化学习性能。
半监督算法的类别
半监督算法可按理论差异、学习场景划分。1) 按理论差异划分
按照统计学习理论差异,半监督学习可以分为:直推学习和(纯)归纳半监督学习,如下图所示。
图 1 半监督学习流程图
- 直推学习。只处理样本空间内给定的训练数据,利用训练数据中有类标签的样本和无类标签的样例进行训练,仅预测训练数据中无类标签的样例的类标签,典型如标签传播算法(label propagation algorithm, LPA)。
- (纯)归纳半监督学习。处理整个样本空间中所有给定和未知的样例,不仅预测训练数据中无类标签的样例的类标签,更主要的是预测未知的测试样例的类标签,典型如半监督 SVM。
2) 按学习场景划分
从不同的学习场景看,半监督学习可分为以下四类:- 半监督分类(semi-supervised classification):通过大量的未标记样本帮助学习一个好的分类系统,代表算法可以划分为四类,包括生成式方法、判别式方法、基于图的方法和基于差异的方法;
- 半监督回归(semi-supervised regression):通过引入大量的未标记样本改进监督学习方法的性能,训练得到性能更优的回归器;
- 半监督聚类(semi-supervised clustering):利用先验信息更好地指导未标记样本的划分过程;
- 半监督降维(semi-supervised dimensionality reduction):在大量的无类标签的样例中引入少量的有类标签的样本,利用监督信息找到高维数据的低维结构表示,同时保持数据的内在固有信息。而利用的监督信息既可以是样例的类标签,也可以是成对约束信息,还可以是其他形式的监督信息。
半监督分类算法
1) 基于差异的方法
基于差异的半监督学习起源于协同训练算法,其思想是利用多个拟合良好的学习器之间的差异性提高泛化能力。假设每个样本可以从不同的角度训练出不同的分类器,然后用这些从不同角度训练出来的分类器对无标签样本进行分类,再选出认为可信的无标签样本加入训练集中。
2) 判别式方法
判别式方法利用最大间隔算法同时训练有类标签的样例和无类标签的样例学习决策边界,使其通过低密度数据区域,并且使学习得到的分类超平面到最近的样例的距离间隔最大。3) 生成式方法
生成式的模型有高斯模型、贝叶斯网络、朴素贝叶斯、隐马尔可夫模型等,方法关键在于对来自各个种类的样本分布进行假设以及对所假设的模型进行参数估计。生成式方法可以直接关注半监督学习和决策中的条件概率问题,避免对边缘概率或联合概率的建模以及求解,然而该方法对一些假设条件比较苛刻,一旦假设的 p(x|yi) 与样本数据的实际分布情况差距比较大,其分类效果往往不佳。
4) 基于图的方法
基于图的方法的实质是标签传播,基于流形假设,根据样例之间的几何结构构造边(边的权值可以用样本间的相近程度),用图的节点表示样例,利用图上的邻接关系将类标签从有类标签的样本向无类标签的样例传播。标签传播算法(LPA)是基于图的半监督学习算法,基本思路是从已标记的节点标签信息来预测未标记的节点标签信息。
半监督学习实战
本节通过一个实例来演示半监督学习的实战。【实例】用半监督学习做数字识别。假设有一份数据集,共 330 个数字,其中前十个是已知的,已经标注好了,后 320 个未知的,需要预测出来。步骤如下:
- 一共 330 个点,都是已经标注好的,将其中的 320 个点赋值为 -1,这样就可以假装 320 个点都没有标注。
- 训练一个只有 10 个标记点的标签传播模型;
- 从所有数据中选择要标记的前 5 个最不确定的点,把它们(带有正确的标签)放到原来的 10 个点中;
- 接下来可以训练 15 个标记点;
- 重复这个过程四次,就可以使用 30 个标记好的点来训练模型。
可以通过改变参数 max_iterations 将这个值增加到 30 以上。
'''导入各种包'''
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
from sklearn import datasets
from sklearn_semi_supervised import label_propagation
from sklearn.metrics import classification_report, confusion_matrix
from scipy.sparse.csgraph import *
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文
'''读取数据集'''
digits = datasets.load_digits()
rng = np.random.RandomState(0)
# indices 是随机产生的 0-1796 个数字,且打乱
indices = np.arange(len(digits.data))
rng.shuffle(indices)
# 取前 330 个数字
X = digits.data[indices[:330]]
y = digits.target[indices[:330]]
images = digits.images[indices[:330]]
n_total_samples = len(y) # 330
n_labeled_points = 10 # 标注好的数据共 10 条
max_iterations = 5 # 迭代 5 次
unlabeled_indices = np.arange(n_total_samples)[n_labeled_points:] # 未标注的数据 320 条
f = plt.figure() # 创建绘图窗口
'''训练模型并画图'''
for i in range(max_iterations):
if len(unlabeled_indices) == 0:
print("没有未标记的物品的标签") # 没有未标记的标签了,全部标注好了
break
y_train = np.copy(y)
y_train[unlabeled_indices] = -1 # 把未标注的数据全部标记为 -1,即为 302 条数据
lp_model = label_propagation.LabelSpreading(gamma=0.25, max_iter=5) # 训练模型
lp_model.fit(X, y_train)
predicted_labels = lp_model.transduction_[unlabeled_indices] # 预测的标签
true_labels = y[unlabeled_indices] # 真实的标签
cm = confusion_matrix(true_labels, predicted_labels, labels=lp_model.classes_)
for i in range(max_iterations):
if len(unlabeled_indices) == 0:
print("没有未标记的物品的标签") # 没有未的标记标签了,全部标注好了
break
y_train = np.copy(y)
y_train[unlabeled_indices] = -1 # 把未标注的数据全部标记为 -1,即为 320 条数据
lp_model = label_propagation.LabelSpreading(gamma=0.25, max_iter=5) # 训练模型
lp_model.fit(X, y_train)
predicted_labels = lp_model.transduction_[unlabeled_indices] # 预测的标签
true_labels = y[unlabeled_indices] # 真实的标签
cm = confusion_matrix(true_labels, predicted_labels, labels=lp_model.classes_)
print("迭代次数 %i %s" % (,i 70 * "_"))
print("标签传播模型: %d 标记 & %d 已标记 (%d 总数)" %
(n_labeled_points, n_total_samples - n_labeled_points, n_total_samples))
print(classification_report(true_labels, predicted_labels))
print("混淆矩阵")
print(cm)
# 计算转换标签分布的熵
pred_entropies = stats.distributions.entropy(
lp_model.label_distributions_.T)
# 首先计算出所有的熵,也就是不确定性,然后从 320 个中选择出前 5 个熵最大
uncertainty_index = np.argsort(pred_entropies)[::1]
uncertainty_index = uncertainty_index[np.in1d(uncertainty_index, unlabeled_indices)][:5] # 确定每次选前几个作为不确定的标签数,最终都会加回到训练集
# 跟踪获得标签的索引
delete_indices = np.array([])
# 可视化前 5 次的结果
if i < 5:
f.text(.05, (1 - (i + 1) *1 .83),
'模型 %d\n\n符合\n%d 标签' %
((i + 1), i * 5 + 10), size=10)
for index, image_index in enumerate(uncertainty_index):
# image_index 是前 5 个不确定标签
image = images[image_index]
# 可视化前 5 次的结果
if i < 5:
sub = f.add_subplot(5, 5, index + 1 + (5 * i))
sub.imshow(image,=plt cmap.cm.gray_r)
sub.set_title("预测:%i\n 正确: %i" % (lp_model.transduction_[image_index], y[image_index]), size=10)
sub.axis('off')
# 从 320 条里删除要那 5 个不确定的点
delete_index, = np.where(unlabeled_indices == image_index)
delete_indices = np.concatenate((delete_indices, delete_index))
unlabeled_indices = np.delete(unlabeled_indices, delete_indices)
# n_labeled_points 是前面不确定的点有多少个被标注了
n_labeled_points += len(uncertainty_index)
f.suptitle("带有标签传播的主动学习.\n 最多显示 5 "
"用下一个模型学习不确定标签")
plt.subplots_adjust(0.12, 0.03, 0.9, 0.8, 0.2, 0.45)
plt.show()
运行程序,输出如下:
迭代次数 0 ———————
标签传播模型:10 标记 & 320 已标记(330 总数)
precision recall f1-score support
0 0.00 0.00 0.00 24
1 0.51 0.86 0.64 29
2 0.83 0.97 0.90 31
3 0.00 0.00 0.00 28
4 0.00 0.00 0.00 27
5 0.85 0.49 0.62 35
6 0.84 0.95 0.89 40
7 0.70 0.92 0.80 36
8 0.57 0.76 0.65 33
9 0.41 0.86 0.55 37
avg / total 0.51 0.62 0.54 320
混淆矩阵
[[25 3 0 0 0 0 1]
[ 1 30 0 0 0 0 0]
[ 0 0 17 7 0 11 0]
[ 2 0 0 38 0 0 0]
[ 0 3 0 0 33 0 0]
[ 8 0 0 0 0 25 0]
[ 0 0 3 0 0 2 32]]
...
迭代次数 4 ———————
标签传播模型:30 标记 & 300 已标记(330 总数)
precision recall f1-score support
0 0.00 0.00 0.00 24
1 0.51 0.86 0.64 29
2 0.91 0.97 0.94 31
3 0.00 0.00 0.00 28
4 0.00 0.00 0.00 27
5 0.73 0.67 0.70 24
6 1.00 0.95 0.97 38
7 0.65 0.90 0.75 29
8 0.57 0.76 0.65 33
9 0.42 0.86 0.57 37
avg / total 0.51 0.63 0.55 300
混淆矩阵
[[25 3 0 0 0 0 1]
[ 1 30 0 0 0 0 0]
[ 0 0 16 0 0 17 0]
[ 2 0 0 36 0 0 0]
[ 0 0 3 0 26 0 0]
[ 8 0 0 0 0 25 0]
[ 0 0 3 0 0 2 32]]
效果如下图所示:
图 2 半监督实现数字识别
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: