K近邻算法详解(附带Python实例)
K 近邻算法是最简单的分类器,没有显式的学习过程或训练过程,属于懒惰学习(lazy learning)。当对数据的分布只有很少或者没有任何先验知识时,K 近邻算法是一个不错的选择。
K近邻算法的原理
K 近邻算法除了可以用来解决分类问题,还可用来解决回归问题。它有着非常简单的原理:当对测试样本进行分类时,首先通过扫描训练样本集,找到与该测试样本最相似的 k 个训练样本,根据这个样本的类别进行投票确定测试样本的类别。也即可通过单个样本与测试样本的相似程度进行加权。如果需要以测试样本对应每类的概率的形式输出,可以通过 k 个样本中不同类别的样本数量分布来进行估计。
K 近邻算法三要素分别为:距离度量、k 值的选择、分类决策规则。
1) 距离度量
特征空间中两个实例点之间的距离是二者相似程度的反映,所以 K 近邻算法中一个重要的问题是计算样本之间的距离,以确定训练样本中哪些样本与测试样本更加接近。在实际应用中,距离计算方法往往需要根据应用的场景和数据本身的特点来选择。当已有的距离方法不能满足实际应用需求时,还需要有针对性地提出适合具体问题的距离度量方法。
设特征空间 χ 是 n 维实数向量空间:
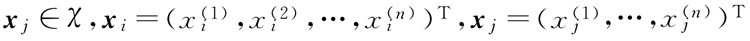
则 xi、xj 的 Lp 距离定义为:
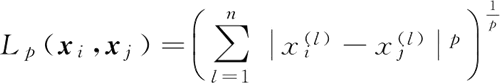
- 当 p=2 时,为欧氏距离(Euclidean distance);
- 当 p=1 时,为曼哈顿距离(Manhattan distance);
- 当 p=∞ 时,为各个坐标距离的最大值。
下图为二维空间中,与原点的 Lp 距离为 1 的点的图形(Lp=1)。
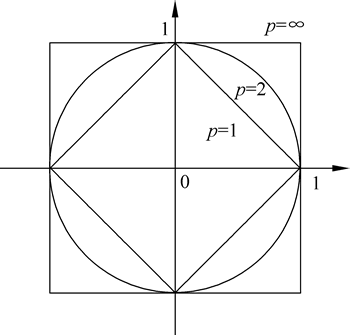
图 3 Lp距离间的关系
2) k值的选择
正常情况下,从 k=1 开始,随着 k 的逐渐增大,K 近邻算法的分类效果会逐渐提升;在增大到某个值后,随着k的进一步增大,K 近邻算法的分类效果会逐渐下降。k 值较小,相当于用较小的邻域中的训练实例进行预测,只有距离近的(相似的)起作用:
- 单个样本影响大;
- “学习”的近似误差(approximation error)会减小,但估计误差(estimation error)会增大;
- 噪声敏感;
- 整体模型变得复杂,容易发生过拟合。
k 值较大,这时距离远的(不相似的)也会起作用:
- 近似误差会增大,但估计误差会减小;
- 整体的模型变得简单。
3) 分类决策规则
分类决策规则一般都是多数表决规则(majority voting rule),为新数据点距离最近的数据点的多数类决定新数据点的类别,实现函数如下:
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,
weights='uniform',
algorithm= '',
leaf_size= '30',
p=2,
metric= 'minkowski',
metric_params=None,
n_jobs=None
)
K近邻算法的实现
K 近邻算法的完整实现过程如下:- 确定 k 的大小和距离计算方法;
-
从训练样本中得到k个与测试最相似的样本:
- 计算测试数据与各个训练数据之间的距离;
- 按照距离的递增关系进行排序;
- 选取距离最小的k个点;
- 确定前 k 个点所在类别的出现频率;
- 返回前 k 个点中出现频率最高的类别作为测试数据的预测分类。
- 根据 k 个组相似样本的类别,通过投票的方式来确定测试样本的类别。
【实例】sklearn的K近邻算法实现。实现步骤如下:
1) 导入包、导入数据。
import numpy as np import matplotlib.pyplot as plt from sklearn import datasets from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score #加载分类模型 from sklearn.linear_model import LogisticRegression from sklearn.svm import SVC iris=datasets.load_iris() X= iris.data[:, :2] #加载Iris数据集的目标 y= iris.target #加载Iris数据集的前两个特征
2) 划分数据。
from sklearn.neighbors import KNeighborsClassifier X_train, X_test, y_train, y_test=train_test_split(X, y, stratify=y, random_state=0)
3) 交叉验证。
from sklearn.model_selection import cross_val_score #导入包
knn_3_clf=KNeighborsClassifier(n_neighbors=3) #实例化对象, k取3, 最近的3个点
knn_5_clf=KNeighborsClassifier(n_neighbors=5)
knn_3_scores=cross_val_score(knn_3_clf, X_train, y_train, cv=10) #训练, 10折
knn_5_scores=cross_val_score(knn_5_clf, X_train, y_train, cv=10)
print("knn_3平均分数:", knn_3_scores.mean(), "knn_3标准:", knn_3_scores.std())
print("knn_3平均分数:", knn_5_scores.mean(), "knn_3标准:", knn_5_scores.std())
knn_3平均分数:0.7983333333333333 knn_3标准:0.09081421817216852
knn_3平均分数:0.8066666666666666 knn_3标准:0.05593205754956987
all_scores=[]
for n_neighbors in range(3, 9, 1):
knn_clf=KNeighborsClassifier(n_neighbors=n_neighbors)
all_scores.append(n_neighbors, cross_val_score(knn_clf, X_train, y_train, cv=10).mean()))
print(sorted(all_scores, key=lambda x:x[0], reverse=True)) #按索引输出
print(sorted(all_scores, key=lambda x:x[1], reverse=True)) #从高分到低分输出
执行结果为:
[(8, 0.7983333333333333), (7, 0.8261111111111111), (6, 0.8233333333333335),
(5, 0.8066666666666666), (4, 0.8511111111111112), (3, 0.7983333333333333)]
[(4, 0.8511111111111112), (7, 0.8261111111111111), (6, 0.8233333333333335),
(5, 0.8066666666666666), (3, 0.7983333333333333), (8, 0.7983333333333333)]
4) 图解。
import mglearn mglearn.plots.plot_knn_classification(n_neighbors=1)
当 k=3 时, 效果如下图所示:
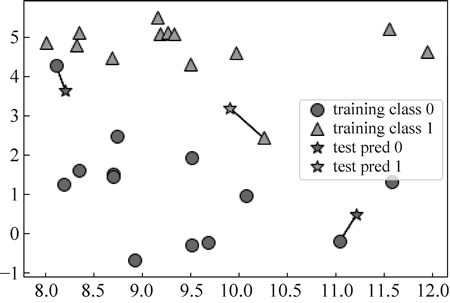
图 4 数据图解效果
5) 分类。
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] #显示中文
X, y=mglearn.datasets.make_forge()
X_train, X_test, y_train, y_test=train_test_split(X, y, random_state=0)
print(X_test.shape)
print(y_test.shape)
print(X_test)
print(y_test) #在测试集上真实的值
from sklearn.neighbors import KNeighborsClassifier
clf=KNeighborsClassifier(n_neighbors=3)
clf.fit(X_train, y_train)
print("测试集预测:", clf.predict(X_test)) #在测试集上预测的值
print("测试集准确性:{:.2f}".format(clf.score(X_test, y_test))) #精度
fig, axes=plt.subplots(1, 3, figsize=(10, 3)) #1行3列
for n_neighbors, ax in zip([1, 3, 9], axes): #n_neighbors=[1, 3, 9], ax=1, 2, 3(循环取值)
clf=KNeighborsClassifier(n_neighbors=n_neighbors).fit(X, y)
mglearn.plots.plot_2d_separator(clf, X, fill=True, eps=0.5, ax=ax, alpha=.4)
#产生可视化的决策边界
mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax)
ax.set_title("{}近邻(s)".format(n_neighbors))
ax.set_xlabel("特征0")
ax.set_ylabel("特征1")
axes[0].legend(loc=3)
X.shape
y.shape
运行程序, 输出如下:
(7, 2)
(7, )
[[11.54155807 5.21116083]
[10.06393839 0.99078055]
[9.49123469 4.33224792]
[8.18378052 1.29564214]
[8.30988863 4.80623966]
[10.24028948 2.45544401]
[8.34468785 1.63824349]]
[1 0 1 0 1 1 0]
测试集预测:[1 0 1 0 1 0 0]
测试集准确性:0.86
(26, )
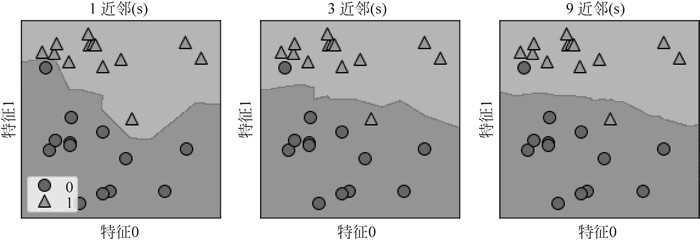
图 5 分类效果
6) 回归。
mglearn.plots.plot_knn_regression(n_neighbors=1)运行程序,效果如下图所示:
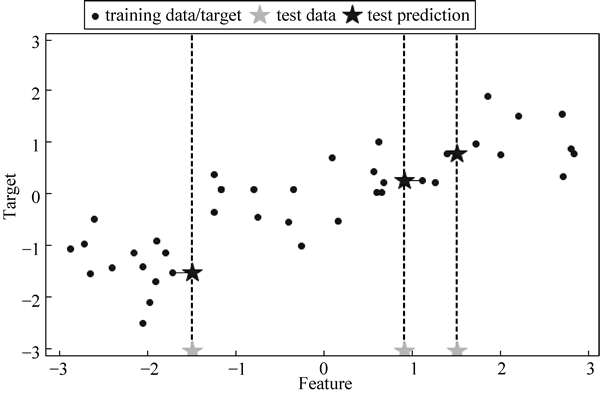
图 6 回归图1
从图 6 中可以看出, 从 test data 中产生 test prediction, 然后找出最近的一个点:
mglearn.plots.plot_knn_regression(n_neighbors=3)运行程序, 效果如下图所示:
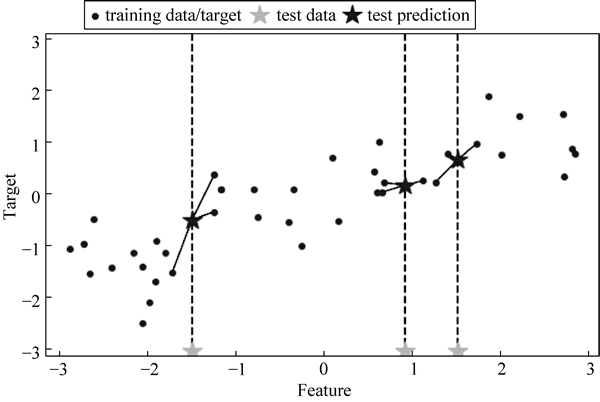
图 7 找出最近的一个点
从图 7 中可以看出, 从 test data 中产生 test prediction, 然后找出最近的 3 个点:
#步骤:导入包、实例化、训练、预测、打分
from sklearn.neighbors import KNeighborsRegressor
X, y=mglearn.datasets.make_wave(n_samples=40)
#将wave数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test=train_test_split(X, y, random_state=0)
#实例化模型, 并将要考虑的邻居数量设置为3
reg=KNeighborsRegressor(n_neighbors=3)
#使用训练数据和训练目标拟合模型
reg.fit(X_train, y_train)
print("测试集预测:\n", reg.predict(X_test))
print("预测集:{:.2f}".format(reg.score(X_test, y_test)))
运行程序, 输出如下:
测试集预测:
[-0.05396539 0.35686046 1.13671923 -1.89415682 -1.13881398 -1.63113382
0.35686046 0.91241374 -0.44680446 -1.13881398]
预测集:0.83
import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
#创建1000个数据点, 均匀分布在-3和3之间
line = np.linspace(-3, 3, 1000).reshape(-1, 1)
for n_neighbors, ax in zip([1, 3, 9], axes):
#使用1、3或9个邻居进行预测
reg = KNeighborsRegressor(n_neighbors=n_neighbors) #实例化
reg.fit(X_train, y_train) #用reg对象的fit方法训练
ax.plot(line, reg.predict(line)) #用reg对象的predict预测
ax.plot(X_train, y_train, '^', c=mglearn.cm2(0), markersize=8)
ax.plot(X_test, y_test, 'v', c=mglearn.cm2(1), markersize=8)
ax.set_title(
"{}近邻(s)\n 训练分数:{:.2f}测试分数:{:.2f}".format(
n_neighbors, reg.score(X_train, y_train), #循环设置标题
reg.score(X_test, y_test)))
ax.set_xlabel("特征")
ax.set_ylabel("目标")
axes[0].legend(["预测模型", "训练数据/目标",
"测试数据/目标"], loc="best") #图例、说明
运行程序, 效果如下图所示: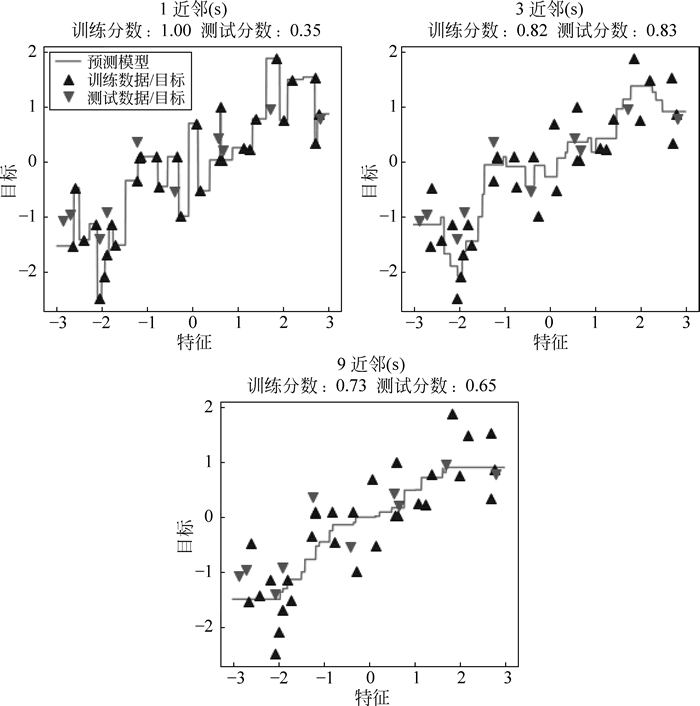
图 8 数据拟合效果
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: