K-Means聚类算法详解(附带实例)
聚类(clustering)是一种寻找数据之间内在结构的技术。聚类把全体数据实例组织成一些相似组,而这些相似组被称作簇。处于相同簇中的数据实例彼此相同,处于不同簇中的实例彼此不同。K-Means、AgglomerativeClustering、DBSCAN、MeanShift、SpectralClustering 等是常用的聚类方法。
K-Means 算法又名 K 均值算法,K-Means 算法中的 K 表示的是聚类为 K 个簇,Means 代表取每一个聚类中数据值的均值作为该簇的中心,或者称为质心,即用每一个类的质心对该簇进行描述。
K-Means 算法预先指定初始聚类数以及初始化聚类中心,按照样本之间的距离大小,把样本集根据数据对象与聚类中心之间的相似度划分为类簇,不断更新聚类中心的位置,不断降低类簇的误差平方和(Sum of Squared Error,SSE),当 SSE 不再变化或目标函数收敛时,聚类结束,得到最终结果。
K-Means 算法的核心思想是:
空间中数据对象与聚类中心间的欧氏距离计算公式为:
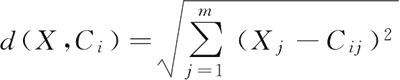
其中,X 为数据对象;Ci 为第 i 个聚类中心;m 为数据对象的维度;Xj、Cij 为 X 和 Ci 的第 j 个属性值。
整个数据集的 SSE 计算公式为:

其中,SSE 的大小表示聚类结果的好坏;k 为簇的个数。
基于原型的聚类即每个聚类都由一个原型表示,原型通常是具有连续特征的相似点的质心(平均值)。虽然 K-Means 算法非常擅长识别具有球形形状的聚类,但这种聚类算法的缺点是必须先验地指定聚类的数量 K。
肘法和轮廓图是评估聚类质量的有用技术,可帮助确定最佳聚类数K。
【实例】使用 sklearn 实现 K-Means 聚类。
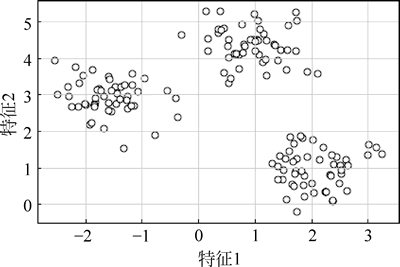
图 3 散点图
接下来,下一个问题是如何衡量对象之间的相似性。可以将相似度定义为距离的反义词,对具有连续特征的样本进行聚类的常用距离是点 x 和 y 之间的平方欧几里得距离。
在 m 维空间中,有:
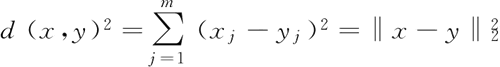
式中,索引 j 指的是实例输入 x 和 y 的第 j 个维度(特征列)。其余部分将使用上标 i 和 j 分别表示实例(数据记录)的索引和集群索引。
接下来,使用 sklearn cluster 模块中的类将它应用到实例数据集:
下面通过代码可视化 K-Means 算法在数据集中识别的集群以及集群质心。存储 cluster_centers_ 拟合 K-Means 对象的属性如下:
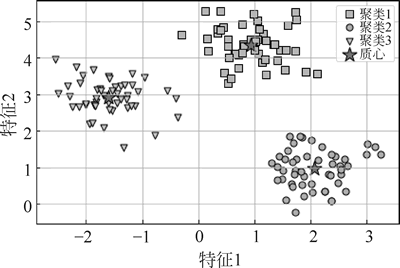
图 5 K-Means聚类效果
在图 5 中,可以看到 K-Means 将 3 个质心放在每个球体的中心。尽管 K-Means 在这个数据集上运行良好,但仍然存在必须先验地指定聚类数量 K 的缺点。
在实际应用中,要选择的集群数量可能并不总是那么明显,尤其是当使用无法可视化的高维数据集时。
K-Means 算法又名 K 均值算法,K-Means 算法中的 K 表示的是聚类为 K 个簇,Means 代表取每一个聚类中数据值的均值作为该簇的中心,或者称为质心,即用每一个类的质心对该簇进行描述。
K-Means算法原理
K-Means 算法是一种典型的基于划分的聚类算法,属于无监督学习算法。K-Means 算法预先指定初始聚类数以及初始化聚类中心,按照样本之间的距离大小,把样本集根据数据对象与聚类中心之间的相似度划分为类簇,不断更新聚类中心的位置,不断降低类簇的误差平方和(Sum of Squared Error,SSE),当 SSE 不再变化或目标函数收敛时,聚类结束,得到最终结果。
K-Means 算法的核心思想是:
- 先从数据集中随机选取K个初始聚类中心 Ci(1≤i≤k),计算其余数据对象与聚类中心 Ci 的欧氏距离,找出离目标数据对象最近的聚类中心 Ci,并将数据对象分配到聚类中心 Ci 所对应的簇中;
- 接着计算每个簇中数据对象的平均值,将该值当作新的聚类中心,进行下一次迭代,直到聚类中心不再变化或达到最大的迭代次数时停止。
空间中数据对象与聚类中心间的欧氏距离计算公式为:
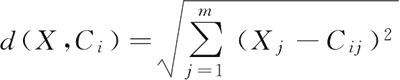
其中,X 为数据对象;Ci 为第 i 个聚类中心;m 为数据对象的维度;Xj、Cij 为 X 和 Ci 的第 j 个属性值。
整个数据集的 SSE 计算公式为:

其中,SSE 的大小表示聚类结果的好坏;k 为簇的个数。
K-Means算法步骤
K-Means 算法的实质是 EM 算法(Expectation-Maximization algorithm,最大期望算法)的模型优化过程,具体步骤如下:- 随机选择 K 个样本作为初始簇类的均值向量。
- 将每个样本数据集划分离它距离最近的簇。
- 根据每个样本所属的簇,更新簇类的均值向量。
- 重复 2、3 步,当达到设置的迭代次数或簇类的均值向量不再改变时,模型构建完成,输出聚类算法结果。
K-Means算法的缺陷
K-Means算法非常简单且使用广泛,但是主要存在以下 4 个缺陷。- K 值需要预先给定,属于预先知识,很多情况下 K 值的估计是非常困难的,对于像计算全部微信用户的交往圈这样的场景就完全没办法用 K-Means 算法进行。对于可以确定K值不会太大但不明确精确的 K 值的场景,可以进行迭代运算,然后找出对应的 K 值,这个值往往能较好地描述有多少个簇类;
- K-Means 算法对初始选取的聚类中心点是敏感的,不同的随机种子点得到的聚类结果完全不同;
- K-Means 算法并不适合所有的数据类型。它不能处理非球形簇、不同尺寸和不同密度的簇;
- 易陷入局部最优解。
使用sklearn进行K-Means聚类
K-Means 算法实现非常容易,并且与其他聚类算法相比,它的计算效率也非常高,这是它受欢迎的原因。K-Means 算法属于基于原型的聚类类别。基于原型的聚类即每个聚类都由一个原型表示,原型通常是具有连续特征的相似点的质心(平均值)。虽然 K-Means 算法非常擅长识别具有球形形状的聚类,但这种聚类算法的缺点是必须先验地指定聚类的数量 K。
肘法和轮廓图是评估聚类质量的有用技术,可帮助确定最佳聚类数K。
【实例】使用 sklearn 实现 K-Means 聚类。
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
# 支持中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 生成数据
X, y = make_blobs(n_samples=150,
n_features=2,
centers=3,
cluster_std=0.5,
shuffle=True,
random_state=0)
# 绘制散点图
plt.scatter(X[:, 0],
X[:, 1],
c='white',
marker='o',
edgecolor='black',
s=50)
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.grid()
plt.tight_layout()
plt.show()
运行程序,数据集由 150 个随机生成的点大致分为 3 个密度较高的区域,通过二维散点图可视化如下图所示。
图 3 散点图
接下来,下一个问题是如何衡量对象之间的相似性。可以将相似度定义为距离的反义词,对具有连续特征的样本进行聚类的常用距离是点 x 和 y 之间的平方欧几里得距离。
在 m 维空间中,有:
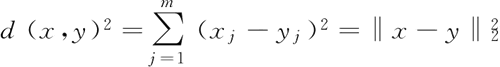
式中,索引 j 指的是实例输入 x 和 y 的第 j 个维度(特征列)。其余部分将使用上标 i 和 j 分别表示实例(数据记录)的索引和集群索引。
接下来,使用 sklearn cluster 模块中的类将它应用到实例数据集:
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3,
init='random',
n_init=10,
max_iter=300,
tol=1e-04,
random_state=0)
y_km = km.fit_predict(X)
当使用欧几里得距离度量将 K-Means 应用于真实世界的数据时,要确保在相同的尺度上测量特征,并在必要时应用 Z-score 标准化或 Min-Max 缩放。下面通过代码可视化 K-Means 算法在数据集中识别的集群以及集群质心。存储 cluster_centers_ 拟合 K-Means 对象的属性如下:
import matplotlib.pyplot as plt
plt.scatter(X[y_km == 0, 0],
X[y_km == 0, 1],
s=50, c='lightgreen',
marker='s', edgecolor='black',
label='聚类1')
plt.scatter(X[y_km == 1, 0],
X[y_km == 1, 1],
s=50, c='orange',
marker='o', edgecolor='black',
label='聚类2')
plt.scatter(X[y_km == 2, 0],
X[y_km == 2, 1],
s=50, c='lightblue',
marker='v', edgecolor='black',
label='聚类3')
plt.scatter(km.cluster_centers_[:, 0],
km.cluster_centers_[:, 1],
s=250, marker='*',
c='red', edgecolor='black',
label='质心')
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.legend(scatterpoints=1)
plt.grid()
plt.tight_layout()
plt.show()
运行程序,效果如下图所示:
图 5 K-Means聚类效果
在图 5 中,可以看到 K-Means 将 3 个质心放在每个球体的中心。尽管 K-Means 在这个数据集上运行良好,但仍然存在必须先验地指定聚类数量 K 的缺点。
在实际应用中,要选择的集群数量可能并不总是那么明显,尤其是当使用无法可视化的高维数据集时。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: