回归分析是什么意思(PyTorch实现)
回归分析就是从一组样本数据出发,确定变量之间的数学关系式,并对这些关系式的可信程度进行各种统计检验,从影响某一特定变量的诸多变量中找出哪些变量的影响显著,哪些不显著。利用所求的关系式,根据一个或几个变量的取值来预测或控制另一个特定变量的取值,同时给出这种预测或控制的精确程度。
线性回归主要用来解决连续性数值预测的问题,它目前在经济、金融、社会、医疗等领域都有广泛的应用。
例如,早期关于吸烟对死亡率和发病率影响的证据来自采用回归分析方法的观察性研究。为了在分析观测数据时减少伪相关,除最感兴趣的变量外,通常研究人员还会在他们的回归模型里包括一些额外变量。例如,假设我们有一个回归模型,在这个回归模型中,吸烟行为是我们最感兴趣的独立变量,其相关变量是经数年观察得到的吸烟者寿命。
研究人员可能将社会经济地位当成一个额外的独立变量,以确保任何经观察所得的吸烟对寿命的影响不是由于教育或收入差异引起的。然而,我们不可能把所有可能混淆结果的变量都加入实证分析中。例如,某种不存在的基因可能会增加人死亡的概率,还会让人的吸烟量增加。因此,比起采用观察数据的回归分析得出的结论,随机对照试验常能产生更令人信服的因果关系证据。
此外,回归分析还在以下诸多方面得到了很好的应用:
线性回归就是能够用一个直线较为精确地描述数据之间的关系。这样当出现新的数据的时候,就能够预测出一个简单的值。线性回归中常见的就是房屋面积和房价的预测问题。只有一个自变量的情况称为一元回归,大于一个自变量的情况称为多元回归。
多元线性回归模型是日常工作中应用频繁的模型,公式如下:
对于误差项有如下几个假设条件:
如果想让我们的预测值尽量准确,就必须让真实值与预测值的差值最小,即让误差平方和最小,用公式来表达如下,具体推导过程可参考相关的资料。
对于误差平方和损失函数的求解方法有很多种,典型的如最小二乘法、梯度下降等。因此,通过以上异同点,总结如下。
最小二乘法的特点:
梯度下降法的特点:
我们知道,因变量 y 值有来自两个方面的影响:
如果一个回归直线预测得非常准确,它就需要让来自 x 的影响尽可能大,而让来自无法预测干扰项的影响尽可能小,也就是说 x 影响占比越高,预测效果就越好。如何定义这些影响,并形成指标,这就涉及总平方和(SSD)、回归平方和(SSR)与残差平方和(SSE)的概念。
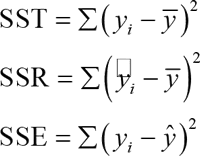
SST、SSR、SSE 三者之间的关系如下图所示:
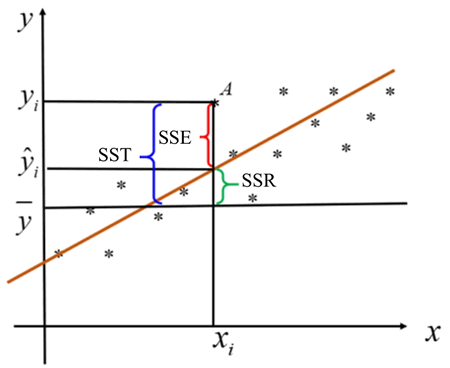
图 2 SST、SSR、SSE三者的关系
它们之间的关系是:SSR 越高,则代表回归预测越准确,观测点越靠近直线,即越大,直线拟合越好。因此,判定系数的定义就自然地引出来了,我们一般称为 R2。
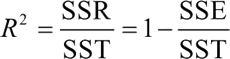
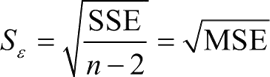
估计标准误差与判定系数相反,Sɛ 反映了预测值与真实值之间误差的大小。误差越小,就说明拟合度越高;相反,误差越大,就说明拟合度越低。
这里我们仅研究部分住房价格影响因素,如房屋的面积、户型、类型、配套设施、地理位置等,具体如下表所示。
操作步骤如下:
① 导入相关第三方库,代码如下:
② 读取训练数据和测试数据,代码如下:
③ 合并数据集,代码如下:
④ 数据预处理,代码如下:
⑤ 数据类型转换,数组转换成张量,代码如下:
⑥ 设置数据迭代器,代码如下:
这样,在训练过程中,每次迭代时,train_data 会返回一个包含 64 个样本的批次。而在测试时,test_data 会按顺序加载数据,不会打乱样本的顺序。这些数据加载器使得在模型训练和测试时能够方便地获取数据批次。
⑦ 设置网络结构,代码如下:
这段代码定义了一个神经网络模型 Net,并使用训练数据和测试数据进行训练和评估。它还计算并打印了每次训练迭代的训练集损失和测试集损失。
⑧ 模型评估与预测,代码如下:
运行建模步骤中的代码,模型的输出如下:
线性回归主要用来解决连续性数值预测的问题,它目前在经济、金融、社会、医疗等领域都有广泛的应用。
例如,早期关于吸烟对死亡率和发病率影响的证据来自采用回归分析方法的观察性研究。为了在分析观测数据时减少伪相关,除最感兴趣的变量外,通常研究人员还会在他们的回归模型里包括一些额外变量。例如,假设我们有一个回归模型,在这个回归模型中,吸烟行为是我们最感兴趣的独立变量,其相关变量是经数年观察得到的吸烟者寿命。
研究人员可能将社会经济地位当成一个额外的独立变量,以确保任何经观察所得的吸烟对寿命的影响不是由于教育或收入差异引起的。然而,我们不可能把所有可能混淆结果的变量都加入实证分析中。例如,某种不存在的基因可能会增加人死亡的概率,还会让人的吸烟量增加。因此,比起采用观察数据的回归分析得出的结论,随机对照试验常能产生更令人信服的因果关系证据。
此外,回归分析还在以下诸多方面得到了很好的应用:
- 客户需求预测:通过海量的买家和卖家交易数据等,对未来商品的需求进行预测;
- 电影票房预测:通过历史票房数据、影评数据等公众数据,对电影票房进行预测;
- 湖泊面积预测:通过研究湖泊面积变化的多种影响因素,构建湖泊面积预测模型;
- 房地产价格预测:利用相关历史数据分析影响商品房价格的因素并进行模型预测;
- 股价波动预测:公司在搜索引擎中的搜索量代表了该股票被投资者关注的程度;
- 人口增长预测:通过历史数据分析影响人口增长的因素,对未来人口数进行预测。
回归分析建模
线性回归(Linear Regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间的关系进行建模的一种分析方式。线性回归就是能够用一个直线较为精确地描述数据之间的关系。这样当出现新的数据的时候,就能够预测出一个简单的值。线性回归中常见的就是房屋面积和房价的预测问题。只有一个自变量的情况称为一元回归,大于一个自变量的情况称为多元回归。
多元线性回归模型是日常工作中应用频繁的模型,公式如下:
y=β0+β1x1+β2x2+…+βkxk+ε其中,x1,…,xk 是自变量,y 是因变量,β0 是截距,β1,…,βk 是变量回归系数,ε 是误差项的随机变量。
对于误差项有如下几个假设条件:
- 误差项 ε 是一个期望为 0 的随机变量。
- 对于自变量的所有值,ε 的方差都相同。
- 误差项 ε 是一个服从正态分布的随机变量,且相互独立。
如果想让我们的预测值尽量准确,就必须让真实值与预测值的差值最小,即让误差平方和最小,用公式来表达如下,具体推导过程可参考相关的资料。
J(β)=∑(y-Xβ)2损失函数只是一种策略,有了策略,我们还要用适合的算法进行求解。在线性回归模型中,求解损失函数就是求与自变量相对应的各个回归系数和截距。有了这些参数,我们才能实现模型的预测(输入 x,输出 y)。
对于误差平方和损失函数的求解方法有很多种,典型的如最小二乘法、梯度下降等。因此,通过以上异同点,总结如下。
最小二乘法的特点:
- 得到的是全局最优解,因为一步到位,直接求极值,所以步骤简单;
- 线性回归的模型假设,这使最小二乘法的优越性前提,否则不能推出最小二乘是最佳(方差最小)的无偏估计。
梯度下降法的特点:
- 得到的是局部最优解,因为是一步一步迭代的,而非直接求得极值;
- 既可以用于线性模型,又可以用于非线性模型,没有特殊的限制和假设条件;
- 在回归分析过程中,还需要进行线性回归诊断,回归诊断是对回归分析中的假设以及数据的检验与分析,主要的衡量值是判定系数和估计标准误差。
1) 判定系数
回归直线与各观测点的接近程度成为回归直线对数据的拟合优度,而评判直线拟合优度需要一些指标,其中一个就是判定系数。我们知道,因变量 y 值有来自两个方面的影响:
- 来自 x 值的影响,也就是我们预测的主要依据。
- 来自无法预测的干扰项 ε 的影响。
如果一个回归直线预测得非常准确,它就需要让来自 x 的影响尽可能大,而让来自无法预测干扰项的影响尽可能小,也就是说 x 影响占比越高,预测效果就越好。如何定义这些影响,并形成指标,这就涉及总平方和(SSD)、回归平方和(SSR)与残差平方和(SSE)的概念。
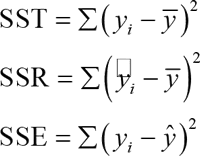
- SST(总平方和):误差的总平方和。
- SSR(回归平方和):由 x 与 y 之间的线性关系引起的 y 变化,反映了回归值的分散程度。
- SSE(残差平方和):除 x 影响外的其他因素引起的 y 变化,反映了观测值偏离回归直线的程度。
SST、SSR、SSE 三者之间的关系如下图所示:

图 2 SST、SSR、SSE三者的关系
它们之间的关系是:SSR 越高,则代表回归预测越准确,观测点越靠近直线,即越大,直线拟合越好。因此,判定系数的定义就自然地引出来了,我们一般称为 R2。
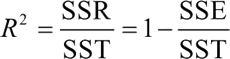
2) 估计标准误差
判定系数 R2 的意义是由 x 引起的影响占总影响的比例来判断拟合程度。当然,我们也可以从误差的角度来评估,也就是用残差 SSE 进行判断。估计标准误差 Sε 是均方残差的平方根,可以度量实际观测点在直线周围散布的情况。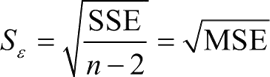
估计标准误差与判定系数相反,Sɛ 反映了预测值与真实值之间误差的大小。误差越小,就说明拟合度越高;相反,误差越大,就说明拟合度越低。
住房价格回归预测
本例利用深度学习的方法对某地的房价进行预测,销售者根据预测的结果选择适合自己的房屋。这里我们仅研究部分住房价格影响因素,如房屋的面积、户型、类型、配套设施、地理位置等,具体如下表所示。
| 字段名称 | 字段说明 |
|---|---|
| Id | 住房编号 |
| Area | 房屋面积 |
| Shape | 房屋户型 |
| Style | 房屋类型 |
| Utilities | 配套设施,如通不通水电气 |
| Neighborhood | 地理位置 |
| Price | 销售价格 |
操作步骤如下:
① 导入相关第三方库,代码如下:
#导入相关库 import torch import numpy as np import pandas as pd from torch.utils.data import DataLoader,TensorDataset import time strat = time.perf_counter()
② 读取训练数据和测试数据,代码如下:
# 读取'./回归分析/train.csv'文件的数据,并赋值给变量 o_train
o_train = pd.read_csv('./回归分析/train.csv')
# 读取'./回归分析/test.csv'文件的数据,并赋值给变量 o_test
o_test = pd.read_csv('./回归分析/test.csv')
这段代码用于读取名为 train.csv 和 test.csv 的文件中的数据,并将其分别赋值给变量 o_train 和 o_test,这样可以在后续的数据分析和回归分析中使用这些数据。③ 合并数据集,代码如下:
# 合并 o_train 和 o_test 数据的'Area'到'Neighborhood'列 all_features = pd.concat((o_train.loc[:, 'Area':'Neighborhood'], o_test.loc[:,'Area':'Neighborhood'])) # 合并 o_train 和 o_test 数据的'Price'列 all_labels = pd.concat((o_train.loc[:, 'Price'], o_test.loc[:, 'Price']))在上述代码中,使用 pd.concat() 函数将两个数据 o_train 和 o_test 的特定列进行合并,loc[:] 选择了数据的所有行,而 'Area':'Neighborhood' 或 'Price' 指定了要合并的列范围。
④ 数据预处理,代码如下:
# 提取所有特征中数值类型的特征索引 numeric_feats = all_features.dtypes[all_features.dtypes!= "object"].index # 提取所有特征中对象类型的特征索引 object_feats = all_features.dtypes[all_features.dtypes == "object"].index # 对数值类型的特征进行标准化处理 all_features[numeric_feats] = all_features[numeric_feats].apply(lambda x: (x - x.mean()) / (x.std())) # 对对象类型的特征进行独热编码 all_features = pd.get_dummies(all_features, prefix=object_feats, dummy_na=True) # 用所有特征的均值填充缺失值 all_features = all_features.fillna(all_features.mean())这段代码主要进行了数据预处理的操作。这样的处理可以帮助模型更好地理解和处理数据,提高模型的准确性和泛化能力。
⑤ 数据类型转换,数组转换成张量,代码如下:
# 将NumPy数组转换为 Torch 张量 train_features = torch.from_numpy(train_features) # 在第 1 个维度上对张量进行 unsqueeze 操作,增加一维 train_labels = torch.from_numpy(train_labels).unsqueeze(1) # 将NumPy数组转换为 Torch 张量 test_features = torch.from_numpy(test_features) # 在第 1 个维度上对张量进行 unsqueeze 操作,增加一维 test_labels = torch.from_numpy(test_labels).unsqueeze(1) # 创建一个包含训练特征和标签的张量数据集 train_set = TensorDataset(train_features, train_labels) # 创建一个包含测试特征和标签的张量数据集 test_set = TensorDataset(test_features, test_labels)将 NumPy 数组转换为 Torch 张量,然后在第一个维度上对张量进行 unsqueeze 操作,增加一维,接着创建包含训练特征和标签的张量数据集 train_set 以及包含测试特征和标签的张量数据集 test_set。
⑥ 设置数据迭代器,代码如下:
#创建一个数据加载器train_data,用于加载训练数据。数据集使用train_set,批大小设置为 64,并且数据会被打乱(shuffle=True) train_data = DataLoader(dataset=train_set, batch_size=64, shuffle=True) #创建另一个数据加载器test_data,用于加载测试数据。数据集使用test_set,批大小同样为 64,但数据不会被打乱(shuffle=False) test_data = DataLoader(dataset=test_set, batch_size=64, shuffle=False)在上述代码中,DataLoader 是 PyTorch 中的一个数据加载器,用于将数据集划分为小批次,并在训练时按顺序循环加载这些批次。
这样,在训练过程中,每次迭代时,train_data 会返回一个包含 64 个样本的批次。而在测试时,test_data 会按顺序加载数据,不会打乱样本的顺序。这些数据加载器使得在模型训练和测试时能够方便地获取数据批次。
⑦ 设置网络结构,代码如下:
class Net(torch.nn.Module): # 定义一个名为 Net 的 torch.nn.Module 子类
def __init__(self, n_feature, n_output): # 构造函数
super(Net, self).__init__() # 调用父类的构造函数
# 定义三层全连接层
self.layer1 = torch.nn.Linear(n_feature, 600) # 输入 n_feature → 600
self.layer2 = torch.nn.Linear(600, 1200) # 600 → 1200
self.layer3 = torch.nn.Linear(1200, n_output) # 1200 → n_output
def forward(self, x): # 前向传播方法
x = self.layer1(x) # 第一层
x = torch.relu(x) # ReLU 激活
x = self.layer2(x) # 第二层
x = torch.relu(x) # ReLU 激活
x = self.layer3(x) # 输出层
return x # 返回结果
# 创建网络实例:输入特征 44,输出 1
net = Net(44, 1)
# 优化器:Adam,学习率 1e-4
optimizer = torch.optim.Adam(net.parameters(), lr=1e-4)
# 损失函数:均方误差
criterion = torch.nn.MSELoss()
# 用于记录训练与测试损失的列表
losses = []
eval_losses = []
# 训练循环 100 轮
for i in range(100):
train_loss = 0.0
net.train() # 训练模式
for tdata, tlabel in train_data: # 遍历训练集
y_ = net(tdata) # 前向传播
loss = criterion(y_, tlabel) # 计算损失
optimizer.zero_grad() # 清零梯度
loss.backward() # 反向传播
optimizer.step() # 更新参数
train_loss += loss.item() # 累计损失
# 记录本轮平均训练损失
losses.append(train_loss / len(train_data))
# 测试阶段
eval_loss = 0.0
net.eval() # 评估模式
with torch.no_grad(): # 不计算梯度
for edata, elabel in test_data: # 遍历测试集
y_ = net(edata)
loss = criterion(y_, elabel)
eval_loss += loss.item()
eval_losses.append(eval_loss / len(test_data))
# 打印当前轮次与损失
print('训练次数:{},训练集损失:{:.4f},测试集损失:{:.4f}'.format(
i, losses[-1], eval_losses[-1]))
这段代码定义了一个神经网络模型 Net,并使用训练数据和测试数据进行训练和评估。它还计算并打印了每次训练迭代的训练集损失和测试集损失。
- 首先,在 __init__ 方法中定义了模型的各层结构。
- 其次,在 forward 方法中定义了前向传播的计算过程。
- 然后,在训练循环中,通过遍历训练数据进行前向传播、计算损失、反向传播和参数更新,并累计训练损失。然后在评估循环中,使用测试数据计算评估损失并累计。
- 最后,打印出每次迭代的训练集损失和测试集损失。
⑧ 模型评估与预测,代码如下:
y_ = net(test_features) # 对测试特征进行网络前向传播
y_pre = y_ * std + mean # 对预测值进行标准化处理
print('测试集预测值:', y_pre.squeeze().detach().cpu().numpy()) # 打印测试集预测值
# 计算并打印模型的平均误差
print('模型平均误差:', abs(y_pre - (test_labels*std + mean)).mean().cpu().item())
end = time.perf_counter() # 获取当前时间
print('模型运行时间:', end - strat) # 打印模型运行时间
这段代码主要是对模型的预测结果进行处理和评估,并输出相关信息。运行建模步骤中的代码,模型的输出如下:
测试集预测值:[12131.775 17357.338 20287.695 18685.883 18266.16 12643.363 13423.217 10104.598 27613.428] 模型平均误差:4383.65234375 模型运行时间:19.38353670000015从结果可以看出,模型平均误差约为 4384 元,由于数据集较小,虽然使用了 CPU 进行建模,但是模型的运行时间也较快,约为 19.38秒。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: