逻辑回归算法(Python实现)
逻辑回归是一种常用的分类算法,尽管名为“回归”,但它其实是用于解决二分类问题的,即目标变量只有两种可能的类别。逻辑回归可以推广到多分类问题,即多项逻辑回归。
逻辑回归的基本思想是,通过线性函数将特征组合起来,并通过逻辑函数(sigmoid 函数),将线性函数的输出映射到 [0,1] 区间,得到每个类别的预测概率。根据预测概率的大小,将样本分到相应的类别。
线性函数的形式为:
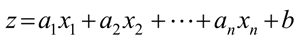
式中,x1, x2,…, xn 为特征;a1,a2,…,an 为各个特征的权重;b 为模型的截距。
逻辑函数的形式为:
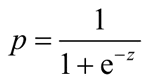
式中,e 为自然对数的底;z 为线性函数的输出。
逻辑回归模型的训练是通过优化算法(如梯度下降算法)找到最佳的权重和截距,使模型的预测概率与实际类别之间的对数损失(log-loss)最小。对数损失的公式为:
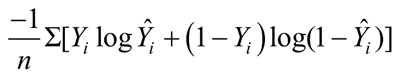
式中, Yi 为实际类别,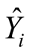 为预测概率, n 为样本数量,Σ 表示对所有样本进行求和。
为预测概率, n 为样本数量,Σ 表示对所有样本进行求和。
逻辑回归模型的优点包括模型简单、输出具有概率意义等,缺点包括只能处理线性可分的问题、对异常值敏感等。通过特征工程和正则化等手段,用户可以使用逻辑回归模型处理更复杂的情况。
假设有一个二元分类问题,模型可以为:
用户可以使用 Scikit-Learn 库的 LogisticRegression 类实现逻辑回归模型。以下是一个简单的例子:
在分类问题中,用户通常不仅关心模型的预测结果,即输入样本为哪一个类别,还关心模型对预测的确定程度。因此,模型的 predict_proba 方法可以提供更多信息,帮助用户理解模型的预测结果。
在使用逻辑回归模型时,用户需要注意几个问题:
在实际问题中,用户可能需要处理更复杂的情况,这时用户可能需要利用更复杂的模型,或使用一些预处理和特征工程的技术,以提高模型的性能。
逻辑回归的基本思想是,通过线性函数将特征组合起来,并通过逻辑函数(sigmoid 函数),将线性函数的输出映射到 [0,1] 区间,得到每个类别的预测概率。根据预测概率的大小,将样本分到相应的类别。
线性函数的形式为:
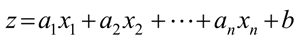
式中,x1, x2,…, xn 为特征;a1,a2,…,an 为各个特征的权重;b 为模型的截距。
逻辑函数的形式为:
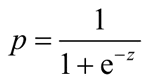
式中,e 为自然对数的底;z 为线性函数的输出。
逻辑回归模型的训练是通过优化算法(如梯度下降算法)找到最佳的权重和截距,使模型的预测概率与实际类别之间的对数损失(log-loss)最小。对数损失的公式为:
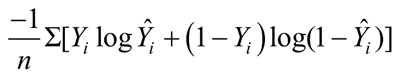
式中, Yi 为实际类别,
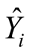 为预测概率, n 为样本数量,Σ 表示对所有样本进行求和。
为预测概率, n 为样本数量,Σ 表示对所有样本进行求和。逻辑回归模型的优点包括模型简单、输出具有概率意义等,缺点包括只能处理线性可分的问题、对异常值敏感等。通过特征工程和正则化等手段,用户可以使用逻辑回归模型处理更复杂的情况。
假设有一个二元分类问题,模型可以为:
p = 1 / (1 + e^(-z))上面这段代码表示逻辑函数,该函数在逻辑回归和深度学习等领域中经常使用。逻辑函数的作用是将输入的连续实值“压缩”到 0~1。如果输入值为正无穷,则输出会趋近于 1;如果输入值为负无穷,则输出会趋近于 0。逻辑函数通常被用来将线性回归的输出转化为概率。
用户可以使用 Scikit-Learn 库的 LogisticRegression 类实现逻辑回归模型。以下是一个简单的例子:
from sklearn.linear_model import LogisticRegression # 初始化逻辑回归模型 lr = LogisticRegression() # 训练模型 lr.fit(X_train, y_train) # 预测 y_pred = lr.predict(X_test) # 预测概率 y_pred_prob = lr.predict_proba(X_test)
- lr=LogisticRegression():初始化 LogisticRegression 模型,并将该模型实例化为 lr;
- lr.fit(X_train, y_train):用训练数据集 (X_train, y_train) 训练模型。模型会学习如何将输入数据 X(特征)映射到输出数据 y(目标变量)。X_train 是输入的特征数据,y_train 是对应的目标变量;
- y_pred=lr.predict(X_test):用训练好的模型对测试集 X_test 进行预测,生成预测结果 y_pred;
- y_pred_prob=lr.predict_proba(X_test):生成测试样本为某种类别的概率。y_pred_prob 是一个二维数组,每一行对应一个输入样本,每一列对应一个类别。每个元素是模型预测输入样本属于此类别的概率。
在分类问题中,用户通常不仅关心模型的预测结果,即输入样本为哪一个类别,还关心模型对预测的确定程度。因此,模型的 predict_proba 方法可以提供更多信息,帮助用户理解模型的预测结果。
在使用逻辑回归模型时,用户需要注意几个问题:
- 由于逻辑回归假设特征和标签的关系是线性的,如果实际关系是非线性的,则逻辑回归可能无法很好地拟合数据;
- 逻辑回归可能受到多重共线性的影响,如果特征之间存在高度相关性,则可能会影响模型的稳定性和解释性;
- 逻辑回归需要足够的数据保证模型的稳定性和准确性,如果数据量过小或类别不平衡,则可能会导致模型性能不佳。
在实际问题中,用户可能需要处理更复杂的情况,这时用户可能需要利用更复杂的模型,或使用一些预处理和特征工程的技术,以提高模型的性能。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: