逻辑分类算法详解(Python实现)
逻辑(logistic)回归是一种广义线性回归(Generalized Linear Model),因此与多重线性回归分析有很多相同之处。
它们的模型形式基本上相同,都具有 w'x+b,其中 w 和 b 是待求参数,其区别在于它们的因变量不同,多重线性回归直接将 w'x+b 作为因变量,即 y=w'x+b,而逻辑回归则通过函数 L 将 w'x+b 对应为一个隐状态 p,p=L(w'x+b),然后根据 p 与 1-p 的大小决定因变量的值。
如果 L 是 logistic 函数,即为 logistic 回归,如果 L 是多项式函数即为多项式回归。
实际中最为常用的就是二分类的逻辑回归。逻辑回归模型的适用条件:
逻辑回归主要在流行病学中应用较多,比较常用的情形是探索某疾病的危险因素,根据危险因素预测某疾病发生的概率,等等。
例如,想探讨胃癌发生的危险因素,可以选择两组人群,一组是胃癌组,另一组是非胃癌组,两组人群肯定有不同的体征和生活方式等。这里的因变量就是是否是胃癌,即“是”或“否”,自变量就可以包括很多了,例如年龄、性别、饮食习惯、幽门螺旋杆菌感染等。自变量既可以是连续的,也可以是分类的。
逻辑回归虽然名字里带“回归”,但是它实际上是一种分类方法,主要用于两分类问题(即输出只有两种,分别代表两个类别),所以利用了逻辑函数(或称为 Sigmoid 函数),函数形式为:
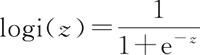
对应的函数图像可用下图来表示:
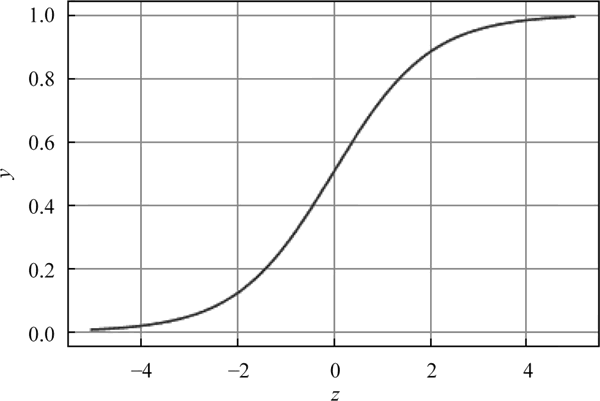
图 2 逻辑回归图像
通过图 2 可以发现逻辑函数是单调递增函数,并且在 z=0 时为回归的基本方程,将回归方程写入其中为:
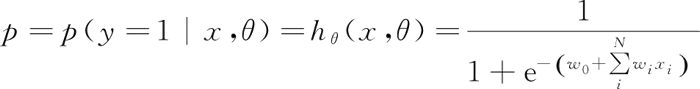
对于模型的训练而言,实质上来说就是利用数据求解出对应模型的特定 ω。从而得到一个针对当前数据的特征逻辑回归模型。而对于多分类而言,将多个二分类的逻辑回归组合,即可实现多分类。
【实例】根据给定的数据实现一个线性模型。
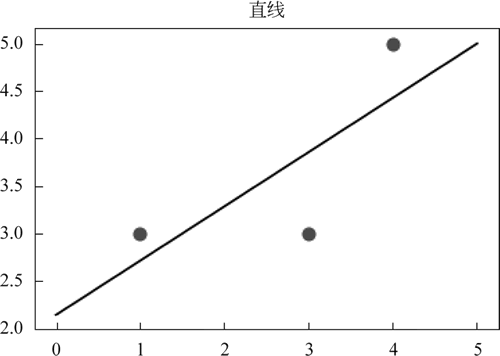
图 4 两个点以及函数
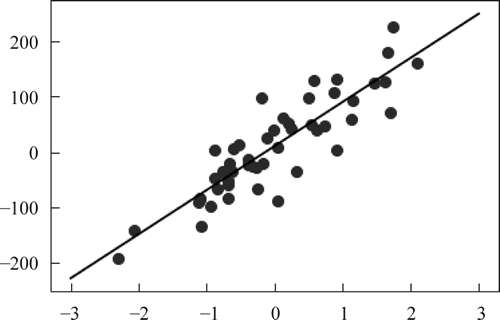
图 5 简单分类效果
通过运行上面的代码可以发现,训练集和测试集的得分均为 1.00,这说明模型的高度拟合,但是这也是因为没有在数据中加入影响因素 noise 导致的,在实际的数据集中会有各种因素的影响,下面代码加入 noise 再进行测试:
在对上述代码运行后,可以发现训练集和测试集间的得分存在一定的差异,这是因为模型过拟合导致的。在现实生活中,拟合存在以下三种情况:
以上就是一个简单的线性模型实现。
【实例】利用逻辑回归对尾花(iris)数据进行分类。
1) 导入函数库。
2) 数据库读取。
3) 数据信息简单查看。
4) 可视化描述。
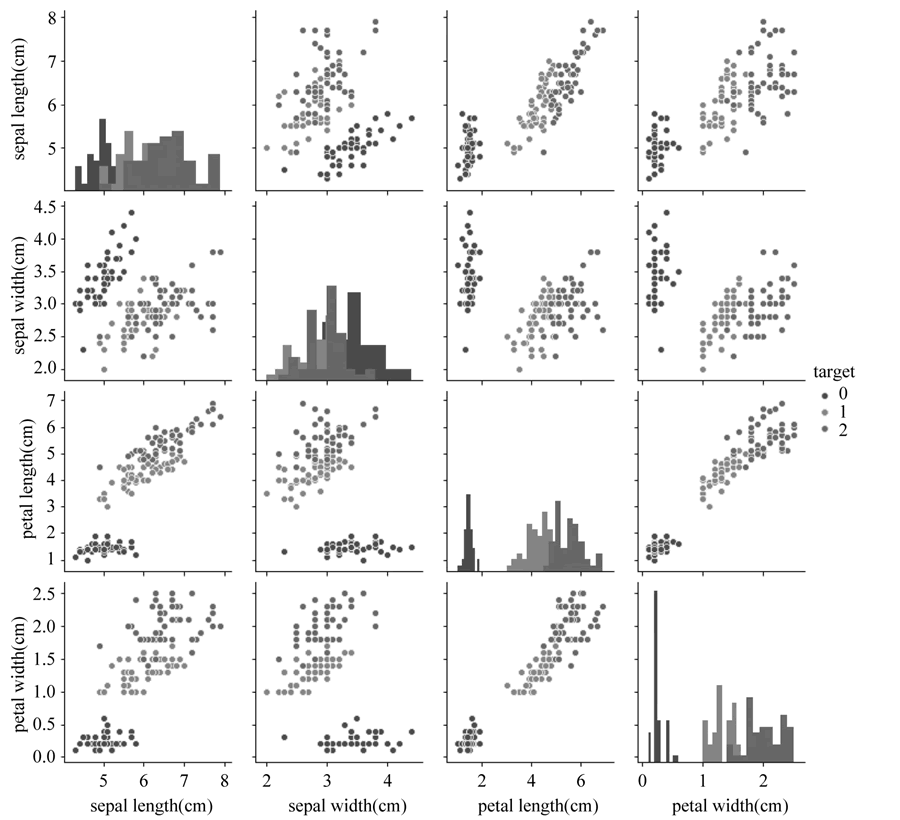
图 6 特征与标签组合的散点可视化
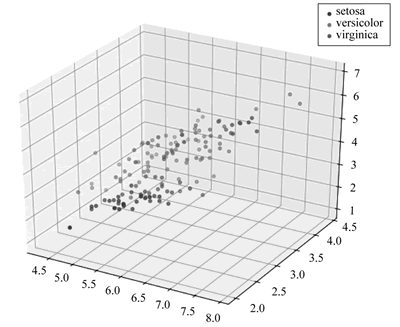
图 7 前三个特征的三维散点图
它们的模型形式基本上相同,都具有 w'x+b,其中 w 和 b 是待求参数,其区别在于它们的因变量不同,多重线性回归直接将 w'x+b 作为因变量,即 y=w'x+b,而逻辑回归则通过函数 L 将 w'x+b 对应为一个隐状态 p,p=L(w'x+b),然后根据 p 与 1-p 的大小决定因变量的值。
如果 L 是 logistic 函数,即为 logistic 回归,如果 L 是多项式函数即为多项式回归。
逻辑回归概述
逻辑回归的因变量可以是二分类的,也可以是多分类的,但是二分类的更为常用,也更加容易解释,多分类可以使用 Softmax 方法进行处理。实际中最为常用的就是二分类的逻辑回归。逻辑回归模型的适用条件:
- 因变量为二分类的分类变量或某事件的发生率,并且是数值型变量。但是需要注意,重复计数现象指标不适用于逻辑回归;
- 残差和因变量都要服从二项分布。二项分布对应的是分类变量,所以不是正态分布,即不需要用最小二乘法,而是用最大似然法来解决方程估计和检验问题;
- 自变量和逻辑概率是线性关系;
- 各观测对象间相互独立。
逻辑回归的主要用途
根据逻辑回归的特点,它的用途主要表现在以下几方面:- 寻找危险因素:寻找某一疾病的危险因素等;
- 预测:根据模型,预测在不同的自变量情况下,发生某病或某种情况的概率有多大;
- 判别:实际上跟预测有些类似,也是根据模型,判断某人患有某病或属于某种情况的概率有多大,也就是看一下这个人有多大的可能性患有某病。
逻辑回归主要在流行病学中应用较多,比较常用的情形是探索某疾病的危险因素,根据危险因素预测某疾病发生的概率,等等。
例如,想探讨胃癌发生的危险因素,可以选择两组人群,一组是胃癌组,另一组是非胃癌组,两组人群肯定有不同的体征和生活方式等。这里的因变量就是是否是胃癌,即“是”或“否”,自变量就可以包括很多了,例如年龄、性别、饮食习惯、幽门螺旋杆菌感染等。自变量既可以是连续的,也可以是分类的。
逻辑回归原理
当 z≥0 时,y≥0.5,分类为 1,当 z<0 时,y<0.5 时,分类为 0,其对应的 y 值可以视为类别 1 的概率预测值。逻辑回归虽然名字里带“回归”,但是它实际上是一种分类方法,主要用于两分类问题(即输出只有两种,分别代表两个类别),所以利用了逻辑函数(或称为 Sigmoid 函数),函数形式为:
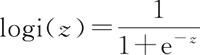
对应的函数图像可用下图来表示:

图 2 逻辑回归图像
通过图 2 可以发现逻辑函数是单调递增函数,并且在 z=0 时为回归的基本方程,将回归方程写入其中为:
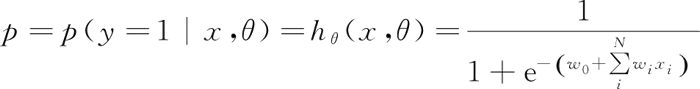
对于模型的训练而言,实质上来说就是利用数据求解出对应模型的特定 ω。从而得到一个针对当前数据的特征逻辑回归模型。而对于多分类而言,将多个二分类的逻辑回归组合,即可实现多分类。
逻辑分类的实现
下面通过一个简单实例来演示逻辑分类问题。【实例】根据给定的数据实现一个线性模型。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
X, y = make_regression(n_samples=100, n_features=2, n_informative=2, random_state=38)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=8)
lr = LinearRegression().fit(X_train, y_train)
print('lr.coef_:{}\n'.format(lr.coef_[:]))
print('lr.intercept_:{}\n'.format(lr.intercept_))
X, y = make_regression(n_samples=50, n_features=1, n_informative=1, noise=50, random_state=1)
reg = LinearRegression()
reg.fit(X, y)
z = np.linspace(-3, 3, 200).reshape(-1, 1)
plt.scatter(X, y, c='b', s=60)
plt.plot(z, reg.predict(z), c='k')
plt.rcParams['font.sans-serif'] = [u'SimHei']
X = [[1], [4], [3]]
y = [3, 5, 3]
lr = LinearRegression().fit(X, y)
z = np.linspace(0, 5, 20)
plt.scatter(X, y, s=80)
plt.plot(z, lr.predict(z.reshape(-1, 1)), c='k')
plt.title('直线')
plt.show()
print('y = {:.3f}'.format(lr.coef_[0]), 'x', '+ {:.3f}'.format(lr.intercept_))
print('\n拟合数据时,求线性方程的系数')
print('直线的系数为:{:.2f}'.format(reg.coef_[0]))
print('直线的截距是:{:.2f}'.format(reg.intercept_))
print('训练集得分:{:.2f}'.format(lr.score(X_test, y_test)))
运行程序,输出如下:
lr.coef_:[70.38592453 7.43213621]
lr.intercep t_:-1.4210854715202004e-14
y=0.571 x+2.143

图 4 两个点以及函数

图 5 简单分类效果
通过运行上面的代码可以发现,训练集和测试集的得分均为 1.00,这说明模型的高度拟合,但是这也是因为没有在数据中加入影响因素 noise 导致的,在实际的数据集中会有各种因素的影响,下面代码加入 noise 再进行测试:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_diabetes
X, y = load_diabetes().data, load_diabetes().target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=8)
lr = LinearRegression().fit(X_train, y_train)
print('训练集得分:{:.2f}'.format(lr.score(X_train, y_train)))
print('测试集得分:{:.2f}'.format(lr.score(X_test, y_test)))
运行程序,输出如下:
训练集得分:0.53
测试集得分:0.?46
在对上述代码运行后,可以发现训练集和测试集间的得分存在一定的差异,这是因为模型过拟合导致的。在现实生活中,拟合存在以下三种情况:
- 欠拟合;
- 拟合;
- 过拟合(这种情况比欠拟合更加麻烦)。
以上就是一个简单的线性模型实现。
【实例】利用逻辑回归对尾花(iris)数据进行分类。
1) 导入函数库。
## 基础函数库 import numpy as np import pandas as pd ## 绘图函数库 import matplotlib.pyplot as plt import seaborn as sns
2) 数据库读取。
##利用sklearn中自带的iris数据作为数据载入,并利用Pandas转换为DataFrame格式 from sklearn.datasets import load_iris data = load_iris() iris_target = data.target iris_features = pd.DataFrame(data=data.data, columns=data.feature_names) #利用Pandas转换为DataFrame格式
3) 数据信息简单查看。
##利用.info()查看数据的整体信息 iris_features.info() <class 'pandas.core.frame.DataFrame'> RangeIndex: 150 entries, 0 to 149 Data columns (total 4 columns): sepal length (cm) 150 non-null float64 sepal width (cm) 150 non-null float64 petal length (cm) 150 non-null float64 petal width (cm) 150 non-null float64 dtypes: float64(4) memory usage: 4.8 KB #利用.head()查看数据的头部 iris_features.head()
4) 可视化描述。
##合并标签和特征信息 iris_all = iris_features.copy() ##进行浅拷贝,防止对于原始数据的修改 iris_all['target'] = iris_target ##特征与标签组合的散点可视化,如图 6 所示

图 6 特征与标签组合的散点可视化
sns.pairplot(data=iris_all,diag_kind='hist', hue= 'target') plt.show() #选取其前三个特征绘制三维散点图,如图 7 所示 from mpl_toolkits.mplot3d import Axes3D fig = plt.figure(figsize=(10,8)) ax = fig.add_subplot(111, projection='3d') iris_all_class0 = iris_all[iris_all['target']==0].values iris_all_class1 = iris_all[iris_all['target']==1].values iris_all_class2 = iris_all[iris_all['target']==2].values #'setosa'(0), 'versicolor'(1), 'virginica'(2) ax.scatter(iris_all_class0[:, 0], iris_all_class0[:, 1], iris_all_class0[:, 2], label='setosa') ax.scatter(iris_all_class1[:, 0], iris_all_class1[:, 1], iris_all_class1[:, 2], label='versicolor') ax.scatter(iris_all_class2[:, 0], iris_all_class2[:, 1], iris_all_class2[:, 2], label='virginica') plt.legend() plt.show()

图 7 前三个特征的三维散点图
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: