逻辑回归算法详解(附带实例,Python实现)
逻辑回归是机器学习中的一种分类算法,虽然名字中带有回归,但是它只是与回归之间有一定的联系。由于算法的简单和高效,在实际中应用非常广泛。
如果数据是有两个指标,可以用平面的点来表示数据,其中一个指标为 x 轴,另一个为 y 轴;如果数据有三个指标,可以用空间中的点表示数据;如果是 p 维(p>3),就是 p 维空间中的点。
从本质上来说,逻辑回归训练后的模型是平面的一条直线(p=2)或平面(p=3)或超平面(p>3)。并且这条线或平面把空间中的散点分成两半,属于同一类的数据大多数分布在曲线或平面的同一侧,如下图所示。

图 1 逻辑回归训练后的模型
如图 1 所示,其中点的个数是样本个数,两种颜色代表两种指标。直线可以看成经这些样本训练后得出的划分样本的直线,对于之后的样本的 p1 与 p2 的值,可以根据这条直线判断它属于哪一类。
这个函数就是 sigmoid 函数,形式为:
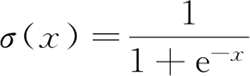
此处可以设函数为:
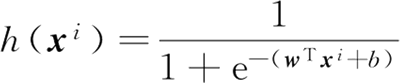
其中,xi 为测试集第 i 个数据,是 p 维列向量:
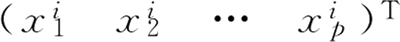
w 是 p 列向量 w=(w1w2…wp)T,为待求参数;b 是一个数,也是待求参数。
用以下 Python 代码实现 sigmoid 函数的图像绘制:
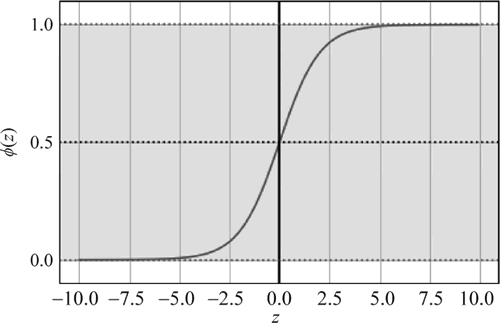
图 5 sigmoid曲线
对于样本 i,其类别为 yi∈(0, 1)。对于样本 i,可以把 h(xi) 看成是一种概率。yi 对应 1 时,概率是 h(xi),即 xi 属于 1 的可能性;yi 对应 0 时,概率是 1-h(xi),即 xi 属于 0 的可能性。构造极大似然函数:
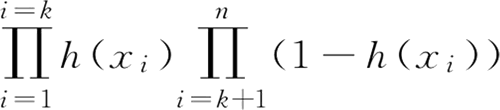
其中,i 从 1~k 属于类别 1 的个数为 k;i 从 k+1~n 属于类别 0 的个数为 n-k。由于 y 是标签 0 或 1 ,所以上面的式子可写成:
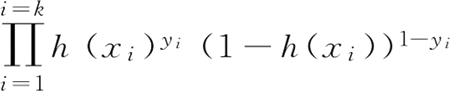
这样不管 y 是 0 还是 1,其中始终有一项会变成 0 次方,也就是 1,和第一个式子是等价的。
为了方便,对式子取对数。因为是求式子的最大值,可以转换成式子乘以 -1,之后求最小值。同时对于 n 个数据,累加后值会很大,之后如果用梯度下降容易导致梯度爆炸。所以可以除以样本总数 n。
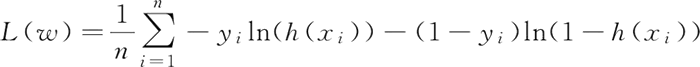
求最小值方法很多,机器学习中常用梯度下降系列方法,也可以采用牛顿法或求导数为零时 w 的数值等。
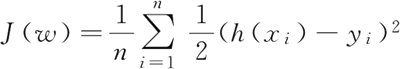
上式是比较直观的,即让预测函数 h(xi) 与实际的分类 1 或 0 越接近越好,也就是损失函数越小越好。
【实例 1】逻辑回归的实现。
【实例 2】利用 Python 中 sklearn 包进行逻辑回归分析。
1) 提出问题,根据已有数据探究“学习时长”与“是否通过考虑”之间关系建立预测模型。
2) 理解数据:
① 导入包和数据:
② 查看数据:
③ 绘制散点图查看数据分布情况:
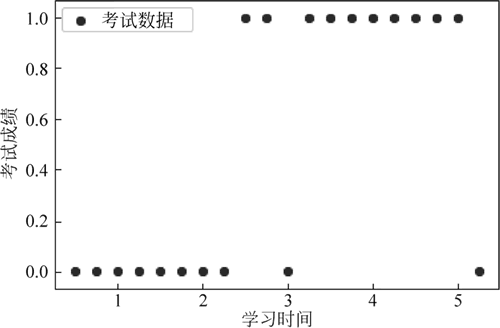
从图中可以看出,当学习时间高于某一阈值时,一般都能够通过考试,下面利用逻辑回归方法建立模型。
3) 构建模型。
① 拆分训练集并利用散点图观察,效果如下图所示:
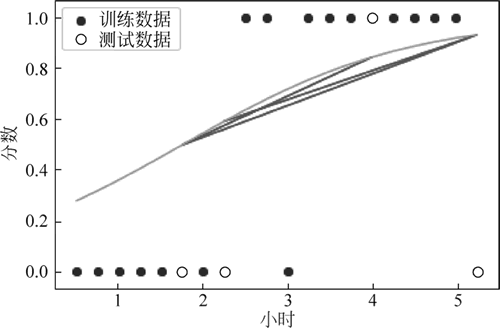
图 11 拆分训练集
② 导入模型:
4) 模型评估:
①模型评分(即准确率):
② 发指定某个点的预测情况:
③ 求出逻辑回归函数并绘制曲线:
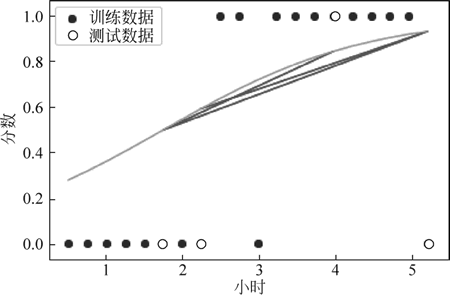
图 12 逻辑回归曲线
④ 得到模型混淆矩阵:
⑤ 绘制模型 ROC 曲线,效果如图 13 所示。
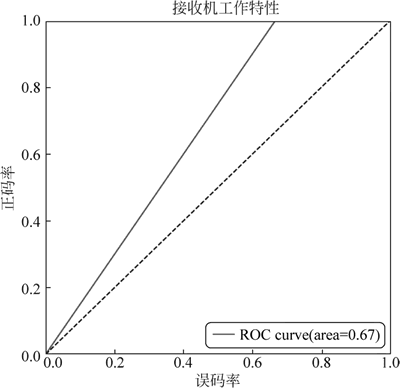
图 13 ROC曲线
逻辑回归所处理的数据
逻辑回归是用来进行分类的。例如,我们给出一个人的[身高,体重]这两个指标,然后判断这个人是属于“胖”还是“瘦”。对于这个问题,可以先测量 n 个人的身高、体重以及对应的指标“胖”“瘦”,分别用 0 和 1 来表示“胖”和“瘦”,把这 n 组数据输入模型进行训练。训练之后再把待分类的一个人的身高、体重输入模型中,看这个人是属于“胖”还是“瘦”。如果数据是有两个指标,可以用平面的点来表示数据,其中一个指标为 x 轴,另一个为 y 轴;如果数据有三个指标,可以用空间中的点表示数据;如果是 p 维(p>3),就是 p 维空间中的点。
从本质上来说,逻辑回归训练后的模型是平面的一条直线(p=2)或平面(p=3)或超平面(p>3)。并且这条线或平面把空间中的散点分成两半,属于同一类的数据大多数分布在曲线或平面的同一侧,如下图所示。

图 1 逻辑回归训练后的模型
如图 1 所示,其中点的个数是样本个数,两种颜色代表两种指标。直线可以看成经这些样本训练后得出的划分样本的直线,对于之后的样本的 p1 与 p2 的值,可以根据这条直线判断它属于哪一类。
逻辑回归算法原理
首先处理二分类问题。由于分成两类,设其中一类标签为 0,另一类为 1。我们需要一个函数,对于输入的每一组数据,都能映射成 0~1 的数。并且如果函数值大于 0.5,就判定属于 1,否则属于 0。而且函数中需要待定参数,通过利用样本训练,使得这个参数能够对训练集中的数据有很准确的预测。这个函数就是 sigmoid 函数,形式为:
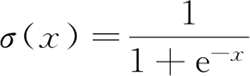
此处可以设函数为:
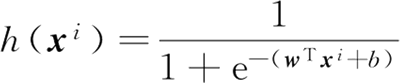
其中,xi 为测试集第 i 个数据,是 p 维列向量:
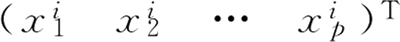
w 是 p 列向量 w=(w1w2…wp)T,为待求参数;b 是一个数,也是待求参数。
用以下 Python 代码实现 sigmoid 函数的图像绘制:
import matplotlib.pyplot as plt
import numpy as np
def sigmoid(z):
return 1.0/(1.0 + np.exp(-z))
z = np.arange(-10,10,0.1)
p = sigmoid(z)
plt.plot(z,p)
#画一条竖直线,如果不设定x的值,则默认是0
plt.axvline(x = 0,color = 'k')
plt.axhspan(0.0,1.0,facecolor = '0.7',alpha = 0.4)
#画一条水平线,如果不设定y的值,则默认是0
plt.axhline(y = 1,ls = 'dotted',color = '0.4')
plt.axhline(y = 0,ls = 'dotted',color = '0.4')
plt.axhline(y = 0.5,ls = 'dotted',color = 'k')
plt.ylim(-0.1,1.1)
#确定y轴的坐标
plt.yticks([0.0,0.5,1.0])
plt.ylabel('$\phi(z)$')
plt.xlabel('z')
ax = plt.gca()
ax.grid(True)
plt.show()
运行程序,效果如下图所示:
图 5 sigmoid曲线
逻辑回归求解参数
下面通过介绍两种方法求解逻辑回归的参数。1) 极大似然估计
极大似然估计是数理统计中参数估计的一种重要方法。其思想是如果一个事件发生了,那么发生这个事件的概率就是最大的。对于样本 i,其类别为 yi∈(0, 1)。对于样本 i,可以把 h(xi) 看成是一种概率。yi 对应 1 时,概率是 h(xi),即 xi 属于 1 的可能性;yi 对应 0 时,概率是 1-h(xi),即 xi 属于 0 的可能性。构造极大似然函数:
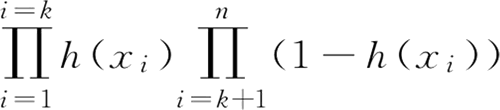
其中,i 从 1~k 属于类别 1 的个数为 k;i 从 k+1~n 属于类别 0 的个数为 n-k。由于 y 是标签 0 或 1 ,所以上面的式子可写成:
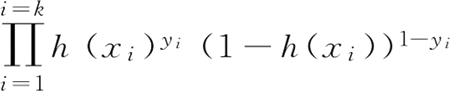
这样不管 y 是 0 还是 1,其中始终有一项会变成 0 次方,也就是 1,和第一个式子是等价的。
为了方便,对式子取对数。因为是求式子的最大值,可以转换成式子乘以 -1,之后求最小值。同时对于 n 个数据,累加后值会很大,之后如果用梯度下降容易导致梯度爆炸。所以可以除以样本总数 n。
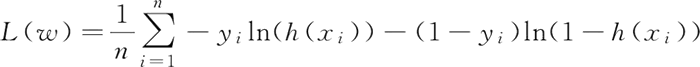
求最小值方法很多,机器学习中常用梯度下降系列方法,也可以采用牛顿法或求导数为零时 w 的数值等。
2) 损失函数
逻辑回归中常用交叉熵损失函数。交叉熵损失函数和上面极大似然法得到的损失函数是相同的,这里不再赘述。另一种也可以采用平方损失函数(均方误差),即: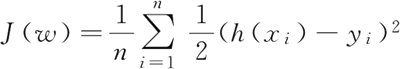
上式是比较直观的,即让预测函数 h(xi) 与实际的分类 1 或 0 越接近越好,也就是损失函数越小越好。
逻辑回归实战
前面已对逻辑回归所处理的数据、算法原理、求解参数等进行了介绍,下面通过两个实例演示如何利用 Python 实现逻辑回归。【实例 1】逻辑回归的实现。
# coding: utf-8
import numpy as np
import math
from sklearn import datasets
from collections import Counter
infinity = float(-2**31)
def sigmoidFormatrix(Xb, thetas):
params = - Xb.dot(thetas)
r = np.zeros(params.shape[0]) # 返回一个 np 数组
for i in range(len(r)):
r[i] = 1 / (1 + math.exp(params[i]))
return r
def sigmoidFormatrix2(Xb, thetas):
params = - Xb.dot(thetas)
r = np.zeros(params.shape[0]) # 返回一个 np 数组
for i in range(len(r)):
r[i] = 1 / (1 + math.exp(params[i]))
if r[i] >= 0.5:
r[i] = 1
else:
r[i] = 0
return r
def sigmoid(Xi, thetas):
params = - np.sum(Xi * thetas)
r = 1 / (1 + math.exp(params))
return r
class LinearLogisticRegression(object):
thetas = None
m = 0
# 训练
def fit(self, X, y, alpha = 0.01, accuracy = 0.00001):
# 插入第一列为1,构成Xb矩阵
self.thetas = np.full((X.shape[1]+1, 0.5))
self.m = X.shape[0]
a = np.full((self.m,1),1)
Xb = np.column_stack((a,X))
dimension = X.shape[1] + 1
# 梯度下降迭代
count = 1
while True:
oldJ = self.costFunc(Xb, y)
c = sigmoidFormatrix(Xb, self.thetas) - y
for j in range(dimension):
self.thetas[j] = self.thetas[j] - alpha * np.sum(c * Xb[:,j])
newJ = self.costFunc(Xb, y)
if newJ == oldJ or math.fabs(newJ - oldJ) < accuracy:
print("代价函数迭代到最小值,退出!")
print("收敛到:",newJ)
break
print("迭代第",count,"次!")
print("代价函数上一次的差:",(newJ - oldJ))
count += 1
# 预测
def costFunc(self, Xb, y):
sum = 0.0
for i in range(self.m):
yPre = sigmoid(Xb[i,:], self.thetas)
# print("yPre:",yPre)
if yPre == 1 or yPre == 0:
return infinity
sum += y[i] * math.log(yPre + (1 - y[i]) * math.log(1 - yPre))
return -1/self.m * sum
def predict(self, X):
a = np.full((len(X),1),1)
Xb = np.column_stack((a,X))
return sigmoidFormatrix2(Xb, self.thetas)
def score(self, X_test, y_test):
y_predict = myLogistic.predict(X_test)
re = (y_test == y_predict)
rel = Counter(re)
a = rel[True] / (rel[True] + rel[False])
return a
# if __name__ == "__main__":
from sklearn.model_selection import train_test_split
iris = datasets.load_iris()
X = iris['data']
y = iris['target']
X = X[y!= 2]
y = y[y!= 2]
X_train,X_test, y_train, y_test = train_test_split(X,y)
myLogistic = LinearLogisticRegression()
myLogistic.fit(X_train, y_train)
y_predict = myLogistic.predict(X_test)
print("参数:",myLogistic.thetas)
print("测试数据准确度:",myLogistic.score(X_test, y_test))
print("训练数据准确度:",myLogistic.score(X_train, y_train))
'''
sklearn 中的逻辑回归
'''
from sklearn.linear_model import LogisticRegression
print("sklearn 中的逻辑回归:")
logr = LogisticRegression()
logr.fit(X_train,y_train)
print("准确度:",logr.score(X_test,y_test))
运行程序,输出如下:
迭代第1次! 代价函数上一次的差:1.92938627909 迭代第2次! 代价函数上一次的差:0.572955749349 迭代第3次! 代价函数上一次的差:-4.91189833803 ... 迭代第239次! 代价函数上一次的差:-1.00784667506e-05 迭代第240次! 代价函数上一次的差:-1.0016786397e-05 代价函数迭代到最小值,退出! 收敛到:0.00339620832005 参数:[ 1.01342939e-03 -8.05476241e-01 -2.19136784e + 00 3.61585103e + 00 1.86218001e + 00] 测试数据准确度:1.0 训练数据准确度:1.0 sklearn中的逻辑回归: 准确度:1.0
【实例 2】利用 Python 中 sklearn 包进行逻辑回归分析。
1) 提出问题,根据已有数据探究“学习时长”与“是否通过考虑”之间关系建立预测模型。
2) 理解数据:
① 导入包和数据:
# 导入包
import warnings
import pandas as pd
import numpy as np
from collections import OrderedDict
import matplotlib.pyplot as plt
warnings.filterwarnings('ignore')
# 创建数据(学习时间与是否通过考试)
dataDict = {'学习时间': list(np.arange(0.50,5.50,0.25)),
'考试成绩':[0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1]}
dataOrDict = OrderedDict(dataDict)
dataDF = pd.DataFrame(dataOrDict)
dataDF.head()
| 学习时间 | 考试成绩 | |
|---|---|---|
| 0 | 0.50 | 0 |
| 1 | 0.75 | 0 |
| 2 | 1.00 | 0 |
| 3 | 1.25 | 0 |
| 4 | 1.50 | 0 |
② 查看数据:
# 查看数据具体形式 dataDF.head() # 查看数据类型及缺失情况 dataDF.info() <class 'pandas.core.frame.DataFrame'> RangeIndex: 20 entries, 0 to 19 Data columns (total 2 columns): 学习时间 20 non-null float64 考试成绩 20 non-null int64 dtypes: float64(1), int64(1) memory usage: 400.0 bytes # 查看描述性统计信息 dataDF.describe()
| 学习时间 | 考试成绩 | |
|---|---|---|
| count | 20.000000 | 20.000000 |
| mean | 2.875000 | 0.500000 |
| std | 1.47902 | 0.512989 |
| min | 0.500000 | 0.000000 |
| 25% | 1.68750 | 0.000000 |
| 50% | 2.87500 | 0.500000 |
| 75% | 4.06250 | 1.000000 |
| max | 5.250000 | 1.000000 |
③ 绘制散点图查看数据分布情况:
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = [u'SimHei']
plt.rcParams['axes.unicode_minus'] = False
#提取特征和标签
exam_X = dataDf['学习时间']
exam_y = dataDf['考试成绩']
#绘制散点图
plt.scatter(exam_X,exam_y,color = 'b',label = '考试数据')
plt.legend(loc = 2)
plt.xlabel('学习时间')
plt.ylabel('考试成绩')
plt.show()
如下图所示:
从图中可以看出,当学习时间高于某一阈值时,一般都能够通过考试,下面利用逻辑回归方法建立模型。
3) 构建模型。
① 拆分训练集并利用散点图观察,效果如下图所示:
#拆分训练集和测试集
from sklearn.cross_validation import train_test_split
exam_X = exam_X.values.reshape(-1,1)
exam_y = exam_y.values.reshape(-1,1)
train_X,test_X,train_y,test_y = train_test_split(exam_X,exam_y,train_size = 0.8)
print('训练集数据大小为',train_X.size,train_y.size)
print('测试集数据大小为',test_X.size,test_y.size)
训练集数据大小为16 16
测试集数据大小为4 4
#散点图观察
plt.scatter(train_X,train_y,color = 'b',label = '训练数据')
plt.scatter(test_X,test_y,color = 'r',label = '测试数据')
plt.legend(loc = 2)
plt.xlabel('小时')
plt.ylabel('分数')
plt.show()

图 11 拆分训练集
② 导入模型:
from sklearn.linear_model import LogisticRegression
modelLR = LogisticRegression()
#训练模型
modelLR.fit(train_X,train_y)
LogisticRegression(C = 1.0,class_weight = None,dual = False,fit_intercept = True,
intercept_scaling = 1,max_iter = 100,multi_class = 'ovr',n_jobs = 1,
penalty = 'l2',random_state = None,solver = 'liblinear',tol = 0.0001,
verbose = 0,warm_start = False)
4) 模型评估:
①模型评分(即准确率):
modelLR.score(test_X,test_y) 0.5
② 发指定某个点的预测情况:
#学习时间确定时,预测为0和1的概率分别为多少? modelLR.predict_proba(3) array([[0.28148368, 0.71851632]]) #学习时间确定时,预测能否通过考试? modelLR.predict(3) array([1],dtype = int64)
③ 求出逻辑回归函数并绘制曲线:
#先求出回归函数y = a + bx,再代入逻辑函数中pred_y = 1/(1 + np.exp(-y))
b = modelLR.coef_
a = modelLR.intercept_
print('该模型对应的回归函数为:1/(1 + exp-(% f + % f * x))'%(a,b))
该模型对应的回归函数为:1/(1 + exp-(-1.332918 + 0.756677 * x))
#画出相应的逻辑回归曲线,如图 12 所示。
plt.scatter(train_X,train_y,color = 'b',label = '训练数据')
plt.scatter(test_X,test_y,color = 'r',label = '测试数据')
plt.plot(test_X,1/(1 + np.exp(-(a + b * test_X))),color = 'r')
plt.plot(exam_X,1/(1 + np.exp(-(a + b * exam_X))),color = 'y')
plt.legend(loc = 2)
plt.xlabel('小时')
plt.ylabel('分数')
plt.show()

图 12 逻辑回归曲线
④ 得到模型混淆矩阵:
from sklearn.metrics import confusion_matrix
#数值处理
pred_y = 1/(1 + np.exp(-(a + b * test_X)))
pred_y = pd.DataFrame(pred_y)
pred_y = round(pred_y,0).astype(int)
#混淆矩阵
confusion_matrix(test_y.astype(str),pred_y.astype(str))
array([[1,2],
[0,1]],dtype = int64)
从混淆矩阵可以看出:
- 该模型的准确率 ACC 为 0.75;
- 真正率 TPR 和假正率 FPR 分别为 0.50 和 0.00,说明该模型对负例的甄别能力更强。
⑤ 绘制模型 ROC 曲线,效果如图 13 所示。
from sklearn.metrics import roc_curve,auc #计算roc和auc
fpr,tpr,threshold = roc_curve(test_y,pred_y) #计算真正率和假正率
roc_auc = auc(fpr,tpr) #计算auc的值
plt.figure()
lw = 2
plt.figure(figsize = (10,10))
plt.plot(fpr,tpr,color = 'r',
lw = lw,label = 'ROC curve(area = % 0.2f)' % roc_auc)
#假正率为横坐标,真正率为纵坐标做曲线
plt.plot([0,1],[0,1],color = 'navy',lw = lw,linestyle = '--')
plt.xlim([0.0,1.0])
plt.ylim([0.0,1.0])
plt.xlabel('误码率')
plt.ylabel('正码率')
plt.title('接收机工作特性')
plt.legend(loc = "lower right")
plt.show()
图 13 中的实线以下部分面积等于 0.75,即误将一个反例划分为正例。
图 13 ROC曲线
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: