套索回归详解(Python实现)
良好的特征对于任何模型都是必需的,但是很多特征需要大量的计算来建立模型。考虑这样一个问题:特征是字典中出现的单词,这些特征可以达到数百万;如果考虑词的组合,这些数字可以达到数十亿;如果对其应用回归算法,模型则需要寻找数十亿个参数,并要花费大量的时间来训练。
特征选择(Feature Selection)是选择有用特征的过程,下面我们使用套索回归(Lasso Regression)来完成这项工作。
如果共有 D 个特征,则必须训练和测试 2D 个模型,如下表所示:
显然,当特征数量较大时,这并不是一个很好的方法。
在该算法中,第一次,训练 D 次模型;第二次,因为一个特征被移动到特征集中,所以训练 D-1 次模型;第三次,使用 D-2 个特征来创建模型。算法最终只剩下一个特征。该特征代表了所有特征(特征集中的 D-1 和可获取的特征集合中的 1,D-1+1=D)。因此,算法的复杂度如下:
贪心算法可以通过不同的方式进行训练。另一种方法是从所有特征开始,逐个删除特征。
岭回归选择特征的一种方法是包含系数大于某一阈值的特征。但是,这可能会错过一些系数权重较低,但在预测中非常重要的特征。
现在尝试通过改变岭目标来完成这项任务。在岭回归中,该模型的成本可写为以下形式:
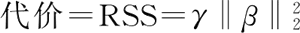
代替 L2 范数,如果使用 L1 范数,则公式为以下形式:
这就是套索回归(Lasso Regression)。γ 是一个调节参数,用于控制系数大小对模型成本造成的影响。
当增加调节参数 γ 的值时,系数开始向零移动。对于非常大的 γ值,模型中剩下的参数非常少(所有其他参数都被消除)。当模型开始训练迭代时,一旦系数命中为零,则保持在该值。
一个方法是在应用回归算法之前对特征进行标准化。通过使用标准化,可以使所有的特征都在相同的范围内,模型中的系数权重将更有意义。
【实例】利用套索回归对波士顿房价数据集进行分析。
当显示某数据的特征(斜率)是 0 的时候,表示是被模型忽略的。这里非 0 的特征数量只有 4 个,说明有过多的特征被忽略了。
为了降低欠拟合,需要降低 alpha 参数,也就是让模型显得“更复杂一点”。除了这么做,还需要增加 max_iter 参数,并适当修改它的值。该值表示运行迭代的最大次数。
但需要注意的是,不能为了继续提高模型的泛化能力而将 alpha 的值改为 0,这样该模型将与 Linear Regression 的结果类似,将出现过拟合的情况。例如:
接下来,就将 alpha 不同值情况下,模型的泛化能力结果用图形展示出来:
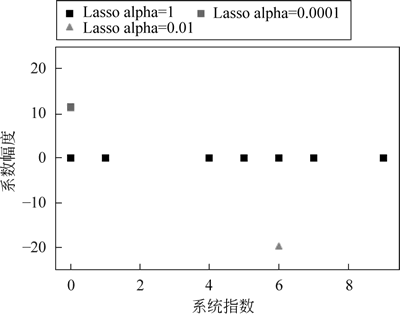
图:套索回归效果图
特征选择(Feature Selection)是选择有用特征的过程,下面我们使用套索回归(Lasso Regression)来完成这项工作。
全子集算法
一种方法是找到所有可能的特征组合并为每个组合的特征训练模型。
For i=1 to特征数量:
获取i特征的所有组合
训练选择的模型
用交叉验证法计算误差
选择误差最小的模型
该算法的运算时间复杂度是指数型。如果特征数量较少,则该算法是有效的;如果特征的数量很大,使用该算法的计算量则是非常大的。如果共有 D 个特征,则必须训练和测试 2D 个模型,如下表所示:
| 特征数量 D | 模型数量 |
|---|---|
| 4 | 16 |
| 8 | 256 |
| 16 | 65536 |
| 32 | 4294967296 |
显然,当特征数量较大时,这并不是一个很好的方法。
贪心算法
贪心算法(Greedy Algorithm)是基于可获得的特征集找到最佳的算法。我们在列表中添加这个特征,并从可获取的列表中删除该特征。
特征集=空
可获取的特征集=所有特征
For i=1 to特征数量:
利用当前最佳特征和特征集对模型进行拟合
从可获取列表中删除选定的特征并将其放在特征集中
使用交叉验证计算误差
选择具有最小误差的特征集
在以上算法中,训练误差将在每一步中得到下降,必须使用验证集方法来确定停止。在该算法中,第一次,训练 D 次模型;第二次,因为一个特征被移动到特征集中,所以训练 D-1 次模型;第三次,使用 D-2 个特征来创建模型。算法最终只剩下一个特征。该特征代表了所有特征(特征集中的 D-1 和可获取的特征集合中的 1,D-1+1=D)。因此,算法的复杂度如下:
D+D-1+D-2+…+3+2+1=O(D)2贪心算法比所有子集算法的计算效率高(D2<<2D)。
贪心算法可以通过不同的方式进行训练。另一种方法是从所有特征开始,逐个删除特征。
正则化
在岭回归中,已经对高系数值的系数进行惩罚以减少模型过拟合。系数的值可以很小,但不是零。如果系数为零,则在回归方程中将不考虑该属性。所以,可以删除这个属性。换句话说,所有非零系数的属性都是可选择的属性。岭回归选择特征的一种方法是包含系数大于某一阈值的特征。但是,这可能会错过一些系数权重较低,但在预测中非常重要的特征。
现在尝试通过改变岭目标来完成这项任务。在岭回归中,该模型的成本可写为以下形式:
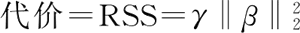
代替 L2 范数,如果使用 L1 范数,则公式为以下形式:
代价=RSS=γ‖β‖1此处 ‖β‖1=|β0|+|β1|+|β2|+…+|βd|。
这就是套索回归(Lasso Regression)。γ 是一个调节参数,用于控制系数大小对模型成本造成的影响。
当增加调节参数 γ 的值时,系数开始向零移动。对于非常大的 γ值,模型中剩下的参数非常少(所有其他参数都被消除)。当模型开始训练迭代时,一旦系数命中为零,则保持在该值。
一个方法是在应用回归算法之前对特征进行标准化。通过使用标准化,可以使所有的特征都在相同的范围内,模型中的系数权重将更有意义。
【实例】利用套索回归对波士顿房价数据集进行分析。
# 导入 numpy
import numpy as np
# 导入数据拆分工具
from sklearn.model_selection import train_test_split
# 导入糖尿病数据集并拆分成训练集和测试集:
from sklearn.datasets import load_diabetes
X, y = load_diabetes().data, load_diabetes().target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=8)
# 导入套索回归
from sklearn.linear_model import Lasso
# 使用套索回归拟合数据
lasso = Lasso().fit(X_train, y_train)
print('套索回归在训练数据集上得分:{:.2f}'.format(lasso.score(X_train, y_train)))
print('套索回归在测试数据集上得分:{:.2f}'.format(lasso.score(X_test, y_test)))
print('套索回归初始特征数:{}'.format(len(lasso.coef_)))
print('套索回归使用的特征数:{}'.format(np.sum(lasso.coef_ != 0)))
print('所有特征:\n', lasso.coef_)
print('所有不为零特征:\n', lasso.coef_ != 0)
运行结果为:
套索回归在训练数据集上得分:0.36
套索回归在测试数据集上得分:0.37
套索回归初始特征数:10
套索回归使用的特征数:3
所有特征:
[ 0. -0. 384.73421807 72.69325545 0.
0. -0. 0. 247.88881314 0. ]
所有不为零特征:
[False False True True False False False True False False]
结果显示,套索回归在训练集和测试集上的表现都不好,说明这个模型存在欠拟合的现象。当显示某数据的特征(斜率)是 0 的时候,表示是被模型忽略的。这里非 0 的特征数量只有 4 个,说明有过多的特征被忽略了。
为了降低欠拟合,需要降低 alpha 参数,也就是让模型显得“更复杂一点”。除了这么做,还需要增加 max_iter 参数,并适当修改它的值。该值表示运行迭代的最大次数。
# 降低 alpha 的值, 增大 max_iter 的值
lasso001 = Lasso(alpha=0.01, max_iter=100000).fit(X_train, y_train)
print('lasso001 在训练集的评估分数:', lasso001.score(X_train, y_train))
print('lasso001 在测试集的评估分数:', lasso001.score(X_test, y_test))
print('lasso001 模型保存的特征数量:', np.sum(lasso001.coef_ != 0))
# 降低 alpha 的值, 增大 max_iter 的值
lasso001 = Lasso(alpha=0.01, max_iter=100000).fit(X_train, y_train)
print('lasso001 在训练集的评估分数:', lasso001.score(X_train, y_train))
print('lasso001 在测试集的评估分数:', lasso001.score(X_test, y_test))
print('lasso001 模型保存的特征数量:', np.sum(lasso001.coef_ != 0))
以上代码中,调小了 alpha 的值,并加大了 max_iter 的值。模型的评估结果表现变得好了许多,并且,使用到的特征数量也有所增加。但需要注意的是,不能为了继续提高模型的泛化能力而将 alpha 的值改为 0,这样该模型将与 Linear Regression 的结果类似,将出现过拟合的情况。例如:
lasso00001 = Lasso(alpha=0.0001, max_iter=100000).fit(X_train, y_train)
print('lasso00001 在训练集的评估分数:', lasso00001.score(X_train, y_train))
print('lasso00001 在测试集的评估分数:', lasso00001.score(X_test, y_test))
print('lasso00001 模型保存的特征数量:', np.sum(lasso00001.coef_ != 0))
lasso00001 在训练集的评估分数: 0.5303811330981303
lasso00001 在测试集的评估分数: 0.45945096837060145
lasso00001 模型保存的特征数量: 10
结果表明,模型在训练集表现相当优异,而在测试集的表现一般,这种现象是因为近拟合造成的,它只能适配于训练的数据,而无法很好地适应于新的数据集。接下来,就将 alpha 不同值情况下,模型的泛化能力结果用图形展示出来:
# 图像显示中文说明
plt.rcParams['font.sans-serif'] = [u'SimHei']
plt.plot(lasso.coef_, 's', label='Lasso alpha=1')
plt.plot(lasso001.coef_, '^', label='Lasso alpha=0.01')
plt.plot(lasso00001.coef_, 's', label='Lasso alpha=0.0001')
plt.legend(ncol=2, loc=(0, 1.05))
plt.ylim(-25, 25)
plt.xlabel('系数指数')
plt.ylabel('系数幅度')
plt.show()
如下图所示:
图:套索回归效果图
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: