线性回归模型详解(Python实现)
线性回归是一种简单、常用的预测模型,用于预测一个连续变量(目标变量)与一个或多个特征(自变量)之间的关系。在这种模型中,假设目标变量与特征之间存在线性关系,即可以通过特征的加权求和预测目标变量,这就是“线性”的由来。
在简单线性回归中,模型只包含一个特征和一个目标变量,公式为:
在多元线性回归中,模型包含两个或两个以上的特征,公式为:
线性回归模型的训练是通过优化算法(如梯度下降算法)找到最佳的权重和截距,使模型的预测值与实际值之间的误差最小,这种误差通常用均方误差衡量,公式为:
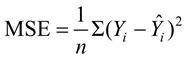 式中,Yi 为实际值,
式中,Yi 为实际值,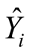 为预测值,n 为样本数量,∑ 表示对所有样本进行求和。
为预测值,n 为样本数量,∑ 表示对所有样本进行求和。
线性回归模型有许多优点,如模型简单、易于理解和解释,但也有一些局限性,如对异常值敏感,只能处理线性关系等。然而,通过特征工程(如特征转换、特征交互等),用户可以使用线性回归模型处理更复杂的情况。
假设有 m 个样本,每个样本有 n 个特征,用户的模型可以写成:
提示,最小化残差平方和是一种在回归分析中常用的目标函数或损失函数,基本思想是找到一组参数,使预测值和实际值之间的差异(残差)平方和最小。
在回归分析中,一个常见的假设是误差向量 ε 服从均值为 0 的正态分布。这样,就可以通过最小化残差平方和找到最优的参数向量 β。
在 y=Xβ+ε 模型中,用户的目标是找到最优的 β,使 ε 的二范数最小。这就是要找到 β,使下式最小:
实际上,最小化残差平方和是在求解以下优化问题:
以下是一个简单的例子:
至此,介绍了线性回归的基本知识和如何在 Python 中实现它。在实际问题中,用户可能需要处理更复杂的情况,如特征之间存在多重共线性,或数据不满足线性假设。在这些情况下,用户可能需要使用其他类型的回归模型,如岭回归、Lasso 回归等,或使用非线性模型。
在简单线性回归中,模型只包含一个特征和一个目标变量,公式为:
Y=aX+b
式中,Y 为目标变量;X 为特征;a 为模型的斜率;b 为模型的截距。在多元线性回归中,模型包含两个或两个以上的特征,公式为:
Y=a1x1+a2x2+⋯+anxn+b
式中,Y 为目标变量;x1,x2,...,xn 为特征;a1,a2,...,an 为各个特征的权重;b 为模型的截距。线性回归模型的训练是通过优化算法(如梯度下降算法)找到最佳的权重和截距,使模型的预测值与实际值之间的误差最小,这种误差通常用均方误差衡量,公式为:
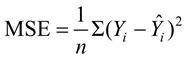
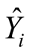 为预测值,n 为样本数量,∑ 表示对所有样本进行求和。
为预测值,n 为样本数量,∑ 表示对所有样本进行求和。线性回归模型有许多优点,如模型简单、易于理解和解释,但也有一些局限性,如对异常值敏感,只能处理线性关系等。然而,通过特征工程(如特征转换、特征交互等),用户可以使用线性回归模型处理更复杂的情况。
假设有 m 个样本,每个样本有 n 个特征,用户的模型可以写成:
y=Xβ+ε式中,y 是 m 维目标变量向量,X 是 m×n 维的特征矩阵,β 是 n 维参数向量,ε 是 m 维误差向量。用户的目标是找到最优的 β,使 ε 的二范数最小,即最小化残差平方和。
提示,最小化残差平方和是一种在回归分析中常用的目标函数或损失函数,基本思想是找到一组参数,使预测值和实际值之间的差异(残差)平方和最小。
在回归分析中,一个常见的假设是误差向量 ε 服从均值为 0 的正态分布。这样,就可以通过最小化残差平方和找到最优的参数向量 β。
在 y=Xβ+ε 模型中,用户的目标是找到最优的 β,使 ε 的二范数最小。这就是要找到 β,使下式最小:
||y-Xβ||2
上面这个式子的结果为残差平方和。这个式子的结果越小,说明用户的预测越接近实际值,也就是说,用户的模型性能越好。实际上,最小化残差平方和是在求解以下优化问题:
min(β||y-Xβ||2)
可以通过最小二乘法直接求得最优的 β。线性回归模型的具体实现
在 Python 中,用户可以使用 Scikit-Learn 库的 LinearRegression 类实现线性回归模型。以下是一个简单的例子:
from sklearn.linear_model import LinearRegression
# 初始化线性回归模型
lr = LinearRegression()
# 训练模型
lr.fit(X_train, y_train)
# 预测
y_pred = lr.predict(X_test)
# 打印参数
print('Coefficients:', lr.coef_)
print('Intercept:', lr.intercept_)
其中,X_train 和 y_train 是训练数据的特征和目标变量,X_test 是测试数据的特征。lr.coef_ 和 lr.intercept_ 分别是模型的系数和截距。至此,介绍了线性回归的基本知识和如何在 Python 中实现它。在实际问题中,用户可能需要处理更复杂的情况,如特征之间存在多重共线性,或数据不满足线性假设。在这些情况下,用户可能需要使用其他类型的回归模型,如岭回归、Lasso 回归等,或使用非线性模型。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: