广义线性回归详解(Python实现)
本节主要从函数模型以及边界决策函数两方面介绍广义线性回归。
假如说,存在训练集得出的 y,y 1=1,y 2=10,y 3=100,我们很难进行一个分类,并且它无法去拟合一个曲面,对于曲面,我们既想使用线性函数进行拟合,又希望拟合过程尽可能好,那么,可以对上式进行变形:
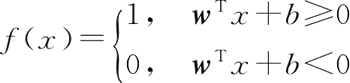
这个函数对于分类是否足够好呢?至少从难易上以及正确率上,一定是不错的。但是,这个函数是不可导的,并且分段梯度始终为 0,显然在后续的处理上是很麻烦的,因此,我们通常不会使用这种方法。这里直接引出 Sigmoid() 函数:
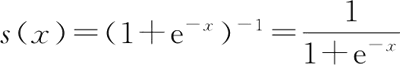
Sigmoid() 函数通常作为逻辑回归、神经网络等算法的默认配置,不过它虽然可以很好地作为一个默认函数,但它也是有缺点的,它的图像如下图所示:
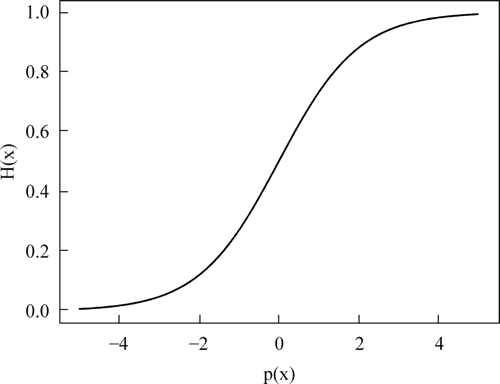
图:Sigmoid()函数图像
假定初始输入值过大,Sigmoid 仍然被限制在(-1,1)范围内,这时,对 Sigmoid() 函数进行求导会发现,Sigmoid() 函数的导数接近 0,我们称为易饱和性,所以我们应该尝试修改初始值,常用的方法就是放缩。
对于 Sigmoid() 函数,第一个缺点显然是容易解决的,但是第二个缺点更为严重。因此常使用双曲正切函数(Hyperbolic Tangent):
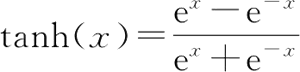
它的图像如下图所示:
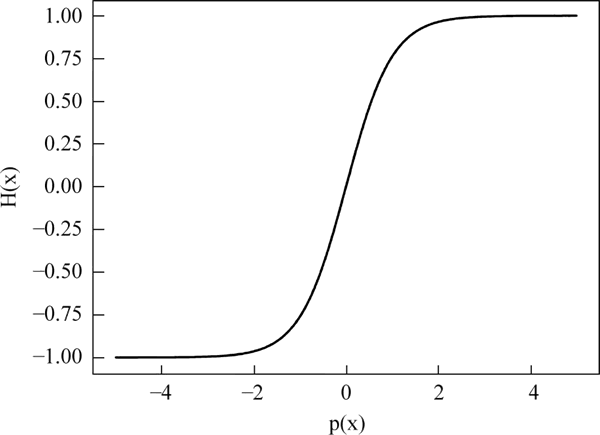
图 5 双曲正切函数图像
函数的期望为 ∫∞tanh(x)=0,但是同样存在易饱和的缺点。事实上,tanh() 函数就是对 Sigmoid() 函数的一个变形:
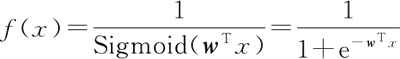
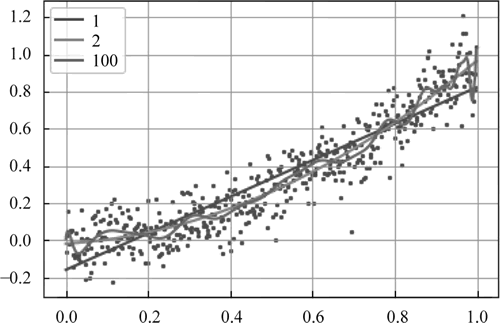
图 7 广义回归拟合效果
显示出的 coef_ 就是多项式参数。如 1 次拟合的结果为:
函数模型
广义线性回归通常也称为 Logistic 回归。先回忆一下线性回归的函数模型:f(x)=wTx+b这个函数可表示的是一条直线,一个平面或者超平面,不过它有致命的缺点,它在处理分类问题时,比如举一个二分类的例子,并不能很好地进行拟合。
假如说,存在训练集得出的 y,y 1=1,y 2=10,y 3=100,我们很难进行一个分类,并且它无法去拟合一个曲面,对于曲面,我们既想使用线性函数进行拟合,又希望拟合过程尽可能好,那么,可以对上式进行变形:
h(x)=g(wTx+b)从整体上来说,通过逻辑回归模型,将在整个实数范围上的 x 映射到有限个点上,这样就实现了对 x 的分类。因为每次利用一个 x,经过逻辑回归分析,就可以将它归入某一类 y 中。
边界决策函数
还是以二分类为例,对于一个二分类问题,最简单的方法就是当 wTx+b≥0,那么 y=1;当 wTx+b<0,那么 y=0。因此我们很快会想到分段函数(称为 Threshold() 函数):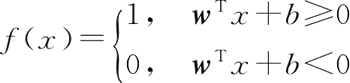
这个函数对于分类是否足够好呢?至少从难易上以及正确率上,一定是不错的。但是,这个函数是不可导的,并且分段梯度始终为 0,显然在后续的处理上是很麻烦的,因此,我们通常不会使用这种方法。这里直接引出 Sigmoid() 函数:
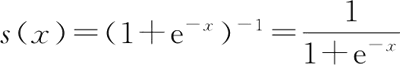
Sigmoid() 函数通常作为逻辑回归、神经网络等算法的默认配置,不过它虽然可以很好地作为一个默认函数,但它也是有缺点的,它的图像如下图所示:

图:Sigmoid()函数图像
假定初始输入值过大,Sigmoid 仍然被限制在(-1,1)范围内,这时,对 Sigmoid() 函数进行求导会发现,Sigmoid() 函数的导数接近 0,我们称为易饱和性,所以我们应该尝试修改初始值,常用的方法就是放缩。
对于 Sigmoid() 函数,第一个缺点显然是容易解决的,但是第二个缺点更为严重。因此常使用双曲正切函数(Hyperbolic Tangent):
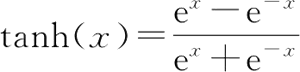
它的图像如下图所示:

图 5 双曲正切函数图像
函数的期望为 ∫∞tanh(x)=0,但是同样存在易饱和的缺点。事实上,tanh() 函数就是对 Sigmoid() 函数的一个变形:
tanh(x)=2Sigmoid(2x)-1不过通常为了加速运算,仅使用 Sigmoid() 函数即可,所以 Logistic() 函数模型就是:
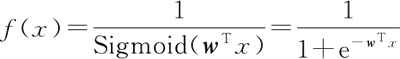
广义回归的实现
本节的实例使用一个二次函数加上随机的扰动来生成 500 个点,然后尝试用 1、2、100 次方的多项式对该数据进行拟合。
import matplotlib.pyplot as plt
import numpy as np
import scipy as sp
from scipy.stats import norm
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn import linear_model
''' 数据生成 '''
x = np.arange(0, 1, 0.002)
y = norm.rvs(0, size=500, scale=0.1)
y = y + x**2
''' 均方误差根 '''
def rmse(y_test, y):
return sp.sqrt(sp.mean((y_test - y) ** 2))
''' 与均值相比的优秀程度,位于[0~1]范围。0 表示不如均值。1 表示完美预测 '''
def R2(y_test, y_true):
return 1 - ((y_test - y_true)**2).sum() / ((y_true - y_true.mean())**2).sum()
def R22(y_test, y_true):
y_mean = np.array(y_true)
y_mean[:] = y_mean.mean()
return 1 - rmse(y_test, y_true) / rmse(y_mean, y_true)
plt.scatter(x, y, s=5)
degree = [1, 2, 100]
y_test = []
y_test = np.array(y_test)
for d in degree:
clf = Pipeline([('poly', PolynomialFeatures(degree=d)),
('linear', LinearRegression(fit_intercept=False))])
clf.fit(x[:, np.newaxis], y)
y_test = clf.predict(x[:, np.newaxis])
print(clf.named_steps['linear'].coef_)
print('rmse=%.2f, R2=%.2f, R22=%.2f, clf.score=%.2f' %
(rmse(y_test, y),
R2(y_test, y),
R22(y_test, y),
clf.score(x[:, np.newaxis], y)))
plt.plot(x, y_test, linewidth=2)
plt.grid()
plt.legend(['1','2','100'], loc='upper left')
plt.show()
运行程序,输出如下:
[-0.16083157 0.98362513] rmse=0.12, R2=0.85, R22=0.61, clf.score=0.85 [-0.01948892 0.13216337 0.85316809] rmse=0.10, R2=0.89, R22=0.67, clf.score=0.89 [ 6.43579247e-03 1.99473917e+01 -3.00770349e+03 1.59988451e+05 -4.65359698e+06 8.64308599e+07 -1.10020819e+09 9.96072148e+09 -6.53953145e+10 3.13441972e+11 -1.08972694e+12 2.67768821e+12 ... 3.85411153e+11 -6.15112350e+11 -1.48802928e+12 -1.84035345e+12 -1.55904918e+12 -6.64790878e+11 6.08514142e+11 1.77891474e+12 2.09861882e+12 9.46642347e+11 -1.36441548e+12 -2.93381938e+12 1.78288101e+12]效果如下图所示:

图 7 广义回归拟合效果
显示出的 coef_ 就是多项式参数。如 1 次拟合的结果为:
rmse=0.10,R2=0.90,R22=0.69,clf.score=0.90
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: