BFS广度优先遍历算法详解(Java实现)
在数据结构中,图的广度优先遍历与树的层次遍历类似。
图的广度优先遍历的思想是:从图的某个顶点 v 出发,首先访问顶点 v,然后按照次序访问顶点 v 未被访问的每个邻接点,接着访问这些邻接点的邻接点,并保证执行先被访问的邻接点的邻接点先访问,后被访问的邻接点的邻接点后访问的顺序,依次访问邻接点的邻接点。
按照这种思想,直到图的所有顶点都被访问过,这样就完成了对图的广度优先遍历。
例如,下面展示了一张图的广度优先遍历过程。
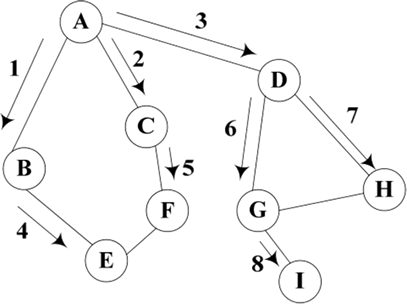
图 1 图的广度优先遍历过程
其中,箭头表示广度优先遍历的方向,图中的数字表示遍历的次序。
图 1 的广度优先遍历过程如下:
至此,图 1 所有的顶点已经被访问完毕。因此,图 1 的广度优先遍历序列为:A、B、C、D、E、F、G、H、I。
图的广度优先遍历的算法实现思想:将图中的所有顶点对应的标志数组 visited[vi] 都初始化为 0,表示顶点未被访问过。从第一个顶点 v0 开始,访问该顶点且将标志列表置为 1。然后将 v0入 队,当队列不为空时,将队头元素(顶点)出队,依次访问该顶点的所有邻接点,并将邻接点依次入队,同时将标志数组对应位置为 1,表示已经访问过。以此类推,直到图中的所有顶点都已经被访问过。
图的广度优先遍历的算法实现如下:
图的广度优先遍历的思想是:从图的某个顶点 v 出发,首先访问顶点 v,然后按照次序访问顶点 v 未被访问的每个邻接点,接着访问这些邻接点的邻接点,并保证执行先被访问的邻接点的邻接点先访问,后被访问的邻接点的邻接点后访问的顺序,依次访问邻接点的邻接点。
按照这种思想,直到图的所有顶点都被访问过,这样就完成了对图的广度优先遍历。
例如,下面展示了一张图的广度优先遍历过程。

图 1 图的广度优先遍历过程
其中,箭头表示广度优先遍历的方向,图中的数字表示遍历的次序。
图 1 的广度优先遍历过程如下:
- 首先访问顶点 A,顶点 A 的邻接点有 B、C、D,然后访问 A 的第一个邻接点 B;
- 访问顶点 A 的第二个邻接点 C,再访问顶点 A 的第三个邻接点 D;
- 顶点 B 的邻接点只有顶点 E,因此访问顶点 E;
- 顶点 C 的邻接点只有 F 且未被访问过,因此访问顶点 F;
- 顶点 D 的邻接点有 G 和 H,且都未被访问过,因此先访问第一个顶点 G,然后访问第二个顶点 H。
- 顶点 E 和 F不存在未被访问的邻接点,顶点 G 未被访问的邻接点有 I,因此访问顶点 I。
至此,图 1 所有的顶点已经被访问完毕。因此,图 1 的广度优先遍历序列为:A、B、C、D、E、F、G、H、I。
广度优先遍历的算法实现
在图的广度优先遍历过程中,同样也需要一个数组 visited[MaxSize] 指示顶点是否被访问过。图的广度优先遍历的算法实现思想:将图中的所有顶点对应的标志数组 visited[vi] 都初始化为 0,表示顶点未被访问过。从第一个顶点 v0 开始,访问该顶点且将标志列表置为 1。然后将 v0入 队,当队列不为空时,将队头元素(顶点)出队,依次访问该顶点的所有邻接点,并将邻接点依次入队,同时将标志数组对应位置为 1,表示已经访问过。以此类推,直到图中的所有顶点都已经被访问过。
图的广度优先遍历的算法实现如下:
public void BFSTraverse(int visited[])
// 从第 1 个顶点出发,按广度优先非递归遍历图
{
final int MaxSize = 20;
int queue[] = new int[MaxSize]; // 定义一个队列
int front = -1; // 初始化队列
int rear = -1;
int v;
for (v = 0; v < vexnum; v++) // 初始化标志位
visited[v] = 0;
v = 0;
visited[v] = 1; // 设置访问标志为 1,表示已经被访问过
System.out.print(vertex[v].data + " ");
rear = (rear + 1) % MaxSize;
queue[rear] = v; // v 入队列
while (front < rear) // 如果队列不空
{
front = (front + 1) % MaxSize;
v = queue[front]; // 队头元素出队赋值给 v
ArcNode p = vertex[v].firstarc; // 遍历序号为 v 的所有邻接点
while (p != null)
{
if (visited[p.adjvex] == 0) // 如果该顶点未被访问过
{
visited[p.adjvex] = 1;
System.out.print(vertex[p.adjvex].data + " ");
rear = (rear + 1) % MaxSize;
queue[rear] = p.adjvex;
}
p = p.nextarc; // p 指向下一个邻接点
}
}
}
假设图的顶点个数为 n,边数(弧)为 e,则采用邻接表实现图的广度优先遍历的时间复杂度为 O(n+e)。图的深度优先遍历和广度优先遍历的结果并不是唯一的,这主要与图存储结点的位置有关。 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: