线性回归算法详解(附带实例,Python实现)
线性回归是机器学习算法中最简单的算法之一,它是监督学习的一种算法。
线性回归算法的主要思想是在给定训练集上学习得到一个线性函数,在损失函数的约束下,求解相关系数,最终在测试集上测试模型的回归效果。
线性回归是利用数理统计中回归分析确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,应用十分广泛。其数学表达式为 y=w′x+e,其中 e 为误差,服从均值为 0 的正态分布。
回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
回归分析就是要找出一个数学模型 y=f(x),使得从 x 估计 y 可以用一个函数式去计算。当 y=f(x) 的形式是一个直线方程时,称为一元线性回归。这个伪方程一般可表示为 y=wx+b。
根据最小平方法,可以从样本数据确定常数项与回归系数的值。b、w 确定后,有一个 x 的观测值,就可得到一个估计值。回归方程是否可靠,估计的误差有多大,都还应经过显著性检验和误差计算。有无显著的相关关系以及样本的大小等是影响回归方程可靠性的因素。
现实世界中的数据总是存在各种误差,例如测量工具的误差、温度数的误差等。而且数据的产生也大部分是一个随机的过程。所以,如果现实世界中存在某些线性关系,那么这个关系也一定是近似的。其一次函数实际如下:
【实例】鸢尾花花瓣长度与宽度的线性回归分析。
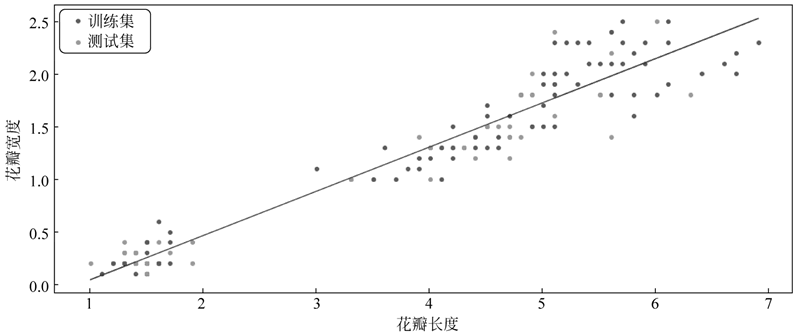
图 1 鸢尾花瓣长度与宽度
测试集的 y 值:[1.5 1.2 2.1 0.2 2.3],预测出来的 y 值的前 5 条数据:[1.77041226 1.30791369 0.21473528 2.27495614 0.2567806]。
在实例程序中,我们对鸢尾花花瓣长度和宽度进行了线性回归,探讨长度与宽度的关系,以及探究鸢尾花的花瓣宽度受长度变化的趋势。但是在现实生活当中的数据是十分复杂的,像这种单因素影响的事物是比较少的,因此我们需要引入多元线性回归来对多个因素的权重进行分配,从而使之与复杂事物相匹配。
事实上,一种现象常常是与多个因素相联系的,由多个自变量的最优组合共同来预测或估计因变量比只用一个自变量进行预测或估计更有效,更符合实际。因此,多元线性回归比一元线性回归的实用意义更大。
假设数据集 D={(x1, y1), (x2, y2), …, (xn, yn)},权值向量 θ=(θ1, θ2, …, θn),配置值为 ε。对权值向量进行转置运算,可以得到:

将所有的特征向量和权值为 1 的一列放在一起,得到 X 的矩阵表示:

对所有的标签进行转置运算,可以得到 y 的矩阵表示:

假设 hθ(x) 为因变量,x1,x2,…,xn 为自变量,并且自变量与因变量之间为线性关系时,则多元线性回归模型为:
假设随机误差项 ε 为 0 时,因变量 hθ(x) 的期望值和自变量 x1,x2,…,xn 的线性方程为:
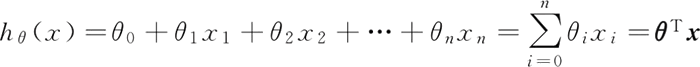
【实例】用多元线性回归探讨 boston 数据集当中每一个因素对房价的影响有多大。
线性回归算法的主要思想是在给定训练集上学习得到一个线性函数,在损失函数的约束下,求解相关系数,最终在测试集上测试模型的回归效果。
线性回归是利用数理统计中回归分析确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,应用十分广泛。其数学表达式为 y=w′x+e,其中 e 为误差,服从均值为 0 的正态分布。
回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
一元线性回归
一元回归的主要任务是从两个相关变量中的一个变量去估计另一个变量,被估计的变量称因变量,可设为 y;估计出的变量称自变量,设为 x。回归分析就是要找出一个数学模型 y=f(x),使得从 x 估计 y 可以用一个函数式去计算。当 y=f(x) 的形式是一个直线方程时,称为一元线性回归。这个伪方程一般可表示为 y=wx+b。
根据最小平方法,可以从样本数据确定常数项与回归系数的值。b、w 确定后,有一个 x 的观测值,就可得到一个估计值。回归方程是否可靠,估计的误差有多大,都还应经过显著性检验和误差计算。有无显著的相关关系以及样本的大小等是影响回归方程可靠性的因素。
现实世界中的数据总是存在各种误差,例如测量工具的误差、温度数的误差等。而且数据的产生也大部分是一个随机的过程。所以,如果现实世界中存在某些线性关系,那么这个关系也一定是近似的。其一次函数实际如下:
y=kx+b+e其中,e 是数据偏离线性的误差,这个误差是服从正态分布的。
【实例】鸢尾花花瓣长度与宽度的线性回归分析。
#导入鸢尾花数据集
from sklearn.datasets import load_iris
#导入用于分割训练集和测试集的类
from sklearn.model_selection import train_test_split
#导入线性回归类
from sklearn.linear_model import LinearRegression
import numpy as np
iris = load_iris()
'''
iris数据集的第三列是鸢尾花长度,第四列是鸢尾花宽度
x和y就是自变量和因变量
reshape(-1,1)就是将iris.data[:,3]由一维数组转置为二维数组,
以便于与iris.data[:,2]进行运算
'''
x,y = iris.data[:,2].reshape(-1,1),iris.data[:,3]
lr = LinearRegression()
'''
train_test_split可以进行训练集与测试集的拆分,
返回值分别为训练集的x,测试集的x,训练集的y,测试集的y,
分别赋值给x_train,x_test,y_train,y_test
test_size:测试集占比
random_state:选定随机种子
'''
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size = 0.25,random_state = 0)
#利用训练集进行机器学习
lr.fit(x_train,y_train)
#权重为lr.coef_
#截距为lr.intercept_
#运用训练出来的模型得出测试集的预测值
y_hat = lr.predict(x_test)
#比较测试集的y值与预测出来的y值的前5条数据
print(y_train[:5])
print(y_hat[:5])
#matplotlib inline
#导入matplotlib模块,进行可视化
from matplotlib import pyplot as plt
plt.rcParams['font.family'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.size'] = 15
plt.figure(figsize = (20,8))
#训练集散点图
plt.scatter(x_train,y_train,color = 'green',marker = 'o',label = '训练集')
#测试集散点图
plt.scatter(x_test,y_test,color = 'orange',marker = 'o',label = '测试集')
#回归线
plt.plot(x,lr.predict(x),'r-')
plt.legend()
plt.xlabel('花瓣长度')
plt.ylabel('花瓣宽度')
plt.show()
运行程序,输出如下,效果如下图所示:
图 1 鸢尾花瓣长度与宽度
测试集的 y 值:[1.5 1.2 2.1 0.2 2.3],预测出来的 y 值的前 5 条数据:[1.77041226 1.30791369 0.21473528 2.27495614 0.2567806]。
在实例程序中,我们对鸢尾花花瓣长度和宽度进行了线性回归,探讨长度与宽度的关系,以及探究鸢尾花的花瓣宽度受长度变化的趋势。但是在现实生活当中的数据是十分复杂的,像这种单因素影响的事物是比较少的,因此我们需要引入多元线性回归来对多个因素的权重进行分配,从而使之与复杂事物相匹配。
多元线性回归
在回归分析中,如果有两个或两个以上的自变量,就称为多元回归。事实上,一种现象常常是与多个因素相联系的,由多个自变量的最优组合共同来预测或估计因变量比只用一个自变量进行预测或估计更有效,更符合实际。因此,多元线性回归比一元线性回归的实用意义更大。
假设数据集 D={(x1, y1), (x2, y2), …, (xn, yn)},权值向量 θ=(θ1, θ2, …, θn),配置值为 ε。对权值向量进行转置运算,可以得到:

将所有的特征向量和权值为 1 的一列放在一起,得到 X 的矩阵表示:

对所有的标签进行转置运算,可以得到 y 的矩阵表示:
y=(y1,y2,…,yn)T由上面三个矩阵,可以得到:

假设 hθ(x) 为因变量,x1,x2,…,xn 为自变量,并且自变量与因变量之间为线性关系时,则多元线性回归模型为:
hθ(x)=θ0+θ1x1+θ2x2+…+θnxn+ε
其中,hθ(x) 为因变量,xi(i=1, 2, …, n)为 n 个自变量,θi(i=1, 2, …, n)为 n+1 个未知参数,ε 为随机误差项。假设随机误差项 ε 为 0 时,因变量 hθ(x) 的期望值和自变量 x1,x2,…,xn 的线性方程为:
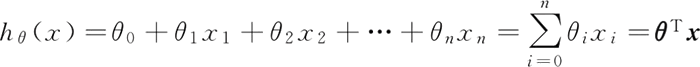
【实例】用多元线性回归探讨 boston 数据集当中每一个因素对房价的影响有多大。
import pandas as pd
import numpy as np
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
boston = load_boston()
#lr继承LinearRegression类
lr = LinearRegression()
#因为boston.data本身就是二维数组,所以无须转置,boston.target是房价
x,y = boston.data,boston.target
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size = 0.15,random_state = 0)
lr.fit(x_train,y_train)
#显示权重,因为有很多因素,所以权重也有很多个
print('显示权重:',lr.coef_)
#显示截距
print('显示截距:',lr.intercept_)
#获取测试集的预测值
y_hat = lr.predict(x_test)
print('测试集的预测值:',y_hat)
运行程序,输出如下:
显示权重:[ -1.23486241e-01 4.05746750e-02 5.95841136e-03 2.17435581e+00
-1.72417774e+01 4.01631980e+00 -4.55531249e-03 -1.39706975e+00
2.83692444e-01 -1.17265285e-02 -1.07074632e+00 1.03277008e-02
-4.55259891e-01]
显示截距:36.1388235171
测试集的预测值:
[ 24.82064867 23.91618148 29.28308707 12.37075596 21.55474268
19.00159781 20.83398791 21.29491264 18.50705994 19.16739973
4.56248891 16.4363932 17.39980225 5.93772537 39.91149633
...
32.60725703 19.23952142 20.18609241 19.40429536 22.9214347
23.02390633 24.03627119 30.3999792 28.63433275 26.38898476
5.84455901]
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: