线性分类器的具体实现(附带Python实例)
在机器学习领域,分类的目标是指将具有相似特征的对象聚集。而一个线性分类器则透过特征的线性组合来做出分类决定,以达到此目的。对象的特征通常被描述为特征值,而在向量中则描述为特征向量。
如果定义 x=(x1, x2, …, xn) 来代表 n 维特征列向量,用 n 维列向量 w=(w1, w2, …,wn) 来代表对应的权重,这称为系数(Coefficient);同时为了避免其过坐标原点这种硬性假设,增加一个截距 (Intercept)b。
这种线性关系可以表达为:
然而,我们所要处理的最简单的二分类问题希望 f∈{0,1};因此需要一个函数把原来的 f∈R 映射到 (0, 1)。于是想到了逻辑(Logistic)函数:
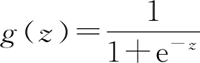
此处的 z∈R 并且 g∈(0, 1),其函数图像如下图所示:
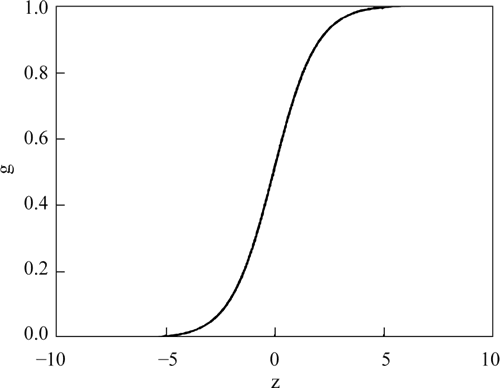
图 2 逻辑函数
【实例】利用线性分类器实现数据聚类。
如果定义 x=(x1, x2, …, xn) 来代表 n 维特征列向量,用 n 维列向量 w=(w1, w2, …,wn) 来代表对应的权重,这称为系数(Coefficient);同时为了避免其过坐标原点这种硬性假设,增加一个截距 (Intercept)b。
这种线性关系可以表达为:
f(w, x, b)=wTx+b
这里的 f∈R,取值范围分布在整个实数域中。然而,我们所要处理的最简单的二分类问题希望 f∈{0,1};因此需要一个函数把原来的 f∈R 映射到 (0, 1)。于是想到了逻辑(Logistic)函数:
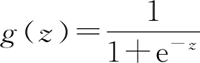
此处的 z∈R 并且 g∈(0, 1),其函数图像如下图所示:

图 2 逻辑函数
【实例】利用线性分类器实现数据聚类。
import random
def matrix_time(x=None, y=None):
sum = 0
for i in range(0, len(x)):
sum += (x[i] * y[i])
print(" α * " + str(y) + "=" + str(sum))
return sum
def matrix_add(x=None, y=None):
result = []
for i in range(0, len(x)):
result.append(x[i] + y[i])
return result
def is_pass_muster(stander=None, data=None):
k = 0
print(" 检验 α 是否能识别全部样本")
for list in data:
m = matrix_time(stander, list)
if (m <= 0):
print(" α * " + str(list) + '=' + str(m) + '<= 0,未能识别全部样本,开始对 α 进行调整')
return False
if (m > 0):
print(" α * " + str(list) + '=' + str(m) + '>0,正确识别样本")
k += 1
if k == len(data):
return True
def fun(x=None):
a = []
while len(a) != 3:
k = random.randint(-9, 9)
if k not in a:
a.append(k)
# a = [-2, 0, -1]
print("初始化 a:" + str(a))
list = []
w = 1
for l in x:
for omega in l:
for i in range(0, len(omega)):
omega[i] *= w
omega.append(w)
list.append(omega)
w *= -1
n = 1
print("第" + str(n) + "轮:")
while not is_pass_muster(stander=a, data=list):
n += 1
print("第" + str(n) + "轮:")
for lt in list:
m = matrix_time(a, lt)
if (m <= 0):
bb = a
a = matrix_add(a, lt)
print(" 未正确识别样本,将 α:" + str(bb) + "调整为:" + str(bb) + "+" + str(lt) + '=' + str(a))
return a
if __name__ == '__main__':
x = [[[0, 0], [0, 1]], [[1, 0], [1, 1]]]
print('输入数据:' + str(x))
a = fun(x)
print('α 全部识别样本:' + str(a))
运行程序,输出如下:
输入数据:[[0, 0], [0, 1], [1, 0], [1, 1]] 初始化 α: [7, -4, -2] 第 1 轮: 检验 α 是否能识别全部样本 α * [0, 0, 1] = -2 α * [0, 0, 1] = -2 < 0, 未能识别全部样本,开始对 α 进行调整 第 2 轮: α * [0, 0, 1] = -2 未正确识别样本,将 α: [7, -4, -2] 调整为:[7, -4, -2] + [0, 0, 1] = [7, -4, -1] α * [0, 1, 1] = -5 未正确识别样本,将 α: [7, -4, -1] 调整为:[7, -4, -1] + [0, 1, 1] = [7, -3, 0] α * [-1, 0, -1] = -7 未正确识别样本,将 α: [7, -3, 0] 调整为:[7, -3, 0] + [-1, 0, -1] = [6, -3, -1] α * [-1, -1, -1] = -2 未正确识别样本,将 α: [6, -3, -1] 调整为:[6, -3, -1] + [-1, -1, -1] = [5, -4, -2] 检验 α 是否能识别全部样本 α * [0, 0, 1] = -2 < 0, 未能识别全部样本,开始对 α 进行调整 第 3 轮: α * [0, 0, 1] = -2 未正确识别样本,将 α: [5, -4, -2] 调整为:[5, -4, -2] + [0, 0, 1] = [5, -4, -1] α * [0, 1, 1] = -5 未正确识别样本,将 α: [5, -4, -1] 调整为:[5, -4, -1] + [0, 1, 1] = [5, -3, 0] α * [-1, 0, -1] = -5 未正确识别样本,将 α: [5, -3, 0] 调整为:[5, -3, 0] + [-1, 0, -1] = [4, -3, -1] α * [-1, -1, -1] = 2 检验 α 是否能识别全部样本 α * [0, 0, 1] = -2 < 0, 未能识别全部样本,开始对 α 进行调整 第 4 轮: α * [0, 0, 1] = -2 未正确识别样本,将 α: [4, -3, -1] 调整为:[4, -3, -1] + [0, 0, 1] = [4, -3, 0] α * [0, 1, 1] = -5 未正确识别样本,将 α: [4, -3, 0] 调整为:[4, -3, 0] + [0, 1, 1] = [4, -2, 1] α * [-1, 0, -1] = -3 未正确识别样本,将 α: [4, -2, 1] 调整为:[4, -2, 1] + [-1, 0, -1] = [3, -2, 0] α * [-1, -1, -1] = 1 检验 α 是否能识别全部样本 α * [0, 0, 1] = -2 < 0, 未能识别全部样本,开始对 α 进行调整 第 5 轮: α * [0, 0, 1] = -2 未正确识别样本,将 α: [3, -2, 0] 调整为:[3, -2, 0] + [0, 0, 1] = [3, -2, 1] α * [0, 1, 1] = -3 未正确识别样本,将 α: [3, -2, 1] 调整为:[3, -2, 1] + [0, 1, 1] = [3, -1, 2] α * [-1, 0, -1] = -3 未正确识别样本,将 α: [3, -1, 2] 调整为:[3, -1, 2] + [-1, 0, -1] = [2, -1, 1] α * [-1, -1, -1] = 1 检验 α 是否能识别全部样本 α * [0, 0, 1] = 0 <= 0, 未能识别全部样本,开始对 α 进行调整 第 6 轮: α * [0, 0, 1] = 0 未正确识别样本,将 α: [2, -1, 1] 调整为:[2, -1, 1] + [0, 0, 1] = [2, -1, 2] α * [0, 1, 1] = -1 未正确识别样本,将 α: [2, -1, 2] 调整为:[2, -1, 2] + [0, 1, 1] = [2, 0, 3] α * [-1, 0, -1] = -3 未正确识别样本,将 α: [2, 0, 3] 调整为:[2, 0, 3] + [-1, 0, -1] = [1, 0, 2] α * [-1, -1, -1] = 0 未正确识别样本,将 α: [1, 0, 2] 调整为:[1, 0, 2] + [-1, -1, -1] = [0, -1, 1] 检验 α 是否能识别全部样本 α * [0, 0, 1] = 0 <= 0, 未能识别全部样本,开始对 α 进行调整 第 7 轮: α * [0, 0, 1] = 0 未正确识别样本,将 α: [-1, -2, 0] 调整为:[-1, -2, 0] + [0, 0, 1] = [-1, -2, 1] α * [0, 1, 1] = -1 未正确识别样本,将 α: [0, -1, 2] 调整为:[0, -1, 2] + [0, 1, 1] = [0, 0, 3] α * [-1, 0, -1] = -3 未正确识别样本,将 α: [0, 0, 3] 调整为:[0, 0, 3] + [-1, 0, -1] = [-1, 0, 2] α * [-1, -1, -1] = 2 检验 α 是否能识别全部样本 α * [0, 0, 1] = 2 > 0, 正确识别样本 α * [0, 1, 1] = 1 > 0, 正确识别样本 α * [-1, 0, -1] = 2 > 0, 正确识别样本 α * [-1, -1, -1] = 2 > 0, 正确识别样本 α 全部识别样本: [-3, 0, 1]
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: