岭回归是什么(Python实现)
岭回归是在最小二乘法的基础上的,所以要了解岭回归,首先要了解最小二乘的回归原理。设有多重线性回归模型 y=xβ+ε,参数 β 的最小二乘估计为:
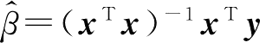
当自变量间存在多重共线性,|xTx|≈0 时,设想 |xTx| 给加上一个正常数矩阵(k>0),那么 |xTx|+kI 接近奇异的程度就会比 |xTx| 接近奇异的程度小得多。
考虑到变量的量纲问题,要先对数据标准化,标准化设计矩阵仍用 x 表示,定义称为岭回归估计,其中,k 称为岭参数。由于假设 x 已经标准化,所以就是自变量样本相关阵。y 可以标准化也可以未标准化,如果 y 也经过标准化,那么计算的实际是标准化岭回归估计。
k 作为 β 的估计应比最小二乘估计稳定,当 k=0 时的岭回归估计就是普通的最小二乘估计。因为岭参数 k 不是唯一确定的,所以得到的岭回归实际上是回归参数的一个估计族。
则岭回归的参数估计为:
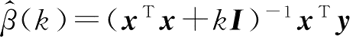
【实例】对给定的数据实现岭回归。
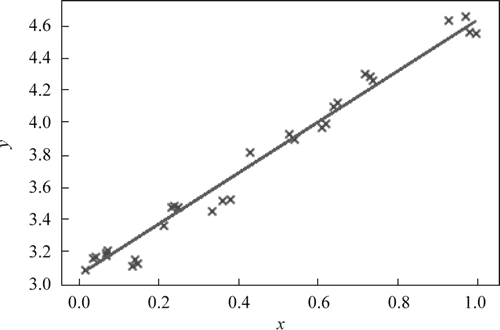
图 1 岭回归效果
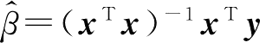
当自变量间存在多重共线性,|xTx|≈0 时,设想 |xTx| 给加上一个正常数矩阵(k>0),那么 |xTx|+kI 接近奇异的程度就会比 |xTx| 接近奇异的程度小得多。
考虑到变量的量纲问题,要先对数据标准化,标准化设计矩阵仍用 x 表示,定义称为岭回归估计,其中,k 称为岭参数。由于假设 x 已经标准化,所以就是自变量样本相关阵。y 可以标准化也可以未标准化,如果 y 也经过标准化,那么计算的实际是标准化岭回归估计。
k 作为 β 的估计应比最小二乘估计稳定,当 k=0 时的岭回归估计就是普通的最小二乘估计。因为岭参数 k 不是唯一确定的,所以得到的岭回归实际上是回归参数的一个估计族。
则岭回归的参数估计为:
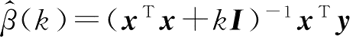
【实例】对给定的数据实现岭回归。
import numpy as np # 快速操作结构数组的工具
import matplotlib.pyplot as plt # 可视化绘制
# Ridge 岭回归, RidgeCV 带有广义交叉验证的岭回归
from sklearn.linear_model import Ridge, RidgeCV
# 样本数据集, 第一列为 x, 第二列为 y, 在 x 和 y 之间建立回归模型
data = [
[0.067732, 3.176513], [0.427810, 3.816464], [0.995731, 4.550095], [0.738336, 4.256571],
[0.981083, 4.560815], [0.526171, 3.929515], [0.378887, 3.526170], [0.033859, 3.156393],
[0.132791, 3.110301], [0.138306, 3.149813], [0.247809, 3.476346], [0.648270, 4.119688],
[0.731209, 4.282233], [0.236833, 3.486582], [0.969788, 4.655492], [0.607492, 3.951622],
[0.358622, 3.514900], [0.147846, 3.125947], [0.637820, 4.094115], [0.230372, 3.476039],
[0.070237, 3.210610], [0.067154, 3.190612], [0.925577, 4.631501], [0.717733, 4.295890],
[0.015371, 3.050528], [0.335070, 3.448080], [0.040486, 3.167440], [0.212575, 3.264266],
[0.617218, 3.993482], [0.541196, 3.891471]
]
# 生成 x 和 y 矩阵
dataMat = np.array(data)
X = dataMat[:, 0:1] # 变量 x
y = dataMat[:, 1] # 变量 y
# 岭回归
model = Ridge(alpha=0.5)
# 通过 RidgeCV 可以设置多个参数值, 算法使用交叉验证获取最佳参数值
model = RidgeCV(alphas=[0.1, 1.0, 10.0])
model.fit(X, y) # 线性回归建模
print('系数矩阵:\n', model.coef_)
print('线性回归模型:\n', model)
# print('交叉验证最佳 alpha 值', model.alpha_) # 只有在使用 RidgeCV 算法时才有效
# 使用模型预测
predicted = model.predict(X)
# 绘制散点图, 参数: x 横轴, y 纵轴
plt.scatter(X, y, marker='x')
plt.plot(X, predicted, c='r')
# 绘制 x 轴和 y 轴坐标
plt.xlabel("x")
plt.ylabel("y")
# 显示图形
plt.show()
运行程序,结果为:
系数矩阵:
[1.57719167]
线性回归模型:
RidgeCV(alphas=[0.1, 1.0, 10.0], cv=None, fit_intercept=True, gcv_mode=None,
normalize=False, scoring=None, store_cv_values=False)
效果如下图所示:
图 1 岭回归效果
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: