动态规划解决01背包问题(图文并茂,C++实现)
所谓 01 背包问题,就是给定 n 种物品,每种物品都有重量 wi 和价值 vi,每种物品都只有一个。另外,背包容量为 W。求解在不超过背包容量的前提下将哪些物品装入背包,才可以使背包内的物品价值之和最大。每种物品只有一个,要么不装,要么装。
假设第 i 阶段处理第 i 种物品,第 i-1 阶段处理第 i-1 种物品,则当处理第 i 种物品时,前 i-1 种物品已处理完毕,只需考虑第 i-1 阶段向第 i 阶段的转移。
用 c[i][j] 表示将前 i 种物品装入容量为 j 的背包可以获得的最大价值。第 i 种物品的处理状态包括以下两种:

若背包容量不足,则肯定不可以装入,价值仍为前 i-1 种物品处理后的结果;若背包容量充足,则考查装入不装入此物品哪种使得背包内的物品价值之和最大。
状态转移方程:
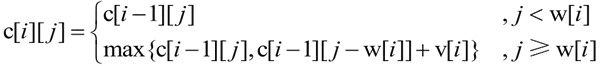
可以用一维数组 x[] 存储解向量,x[i]=1 表示第 i 种物品被装入背包,x[i]=0 表示第 i 种物品未被装入背包:
此时已经得到解向量(x[1],x[2],…,x[n]),直接输出该解向量,也可以仅输出 x[i]=1 的物品序号 i。

1) 初始化。c[i][j] 表示将前 i 种物品装入容量为 j 的背包可以获得的最大价值。初始化数组 c[][] 第 0 行第 0 列为 0。

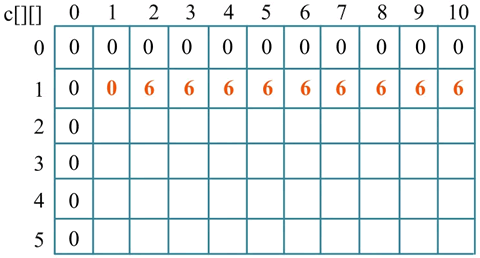
2) 按照状态转移方程处理第 1 种物品(i=1),w[1]=2,v[1]=6,如下图所示。
其中:
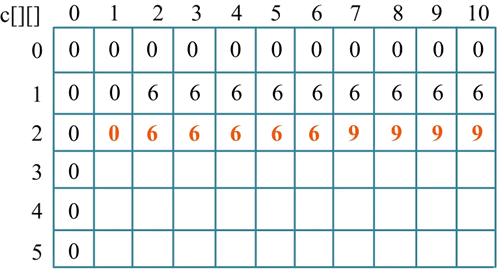
3) 按照状态转移方程处理第 2 种物品(i=2),w[2]=5,v[2]=3,如下图所示。
其中:
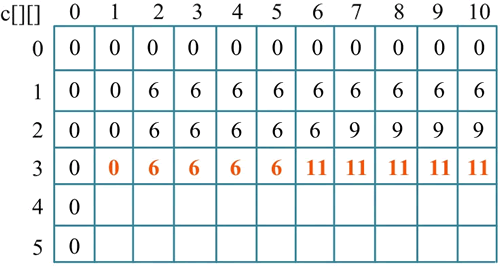
4) 按照状态转移方程处理第 3 种物品(i=3),w[3]=4,v[3]=5,如下图所示。
其中:
5) 按照状态转移方程处理第 4 种物品(i=4),w[4]=2,v[4]=4,如下图所示。

其中:
6) 按照状态转移方程处理第 5 种物品(i=5),w[5]=3,v[5]=6,如下图所示。
其中:
7) 构造最优解:
算法代码:
算法代码:
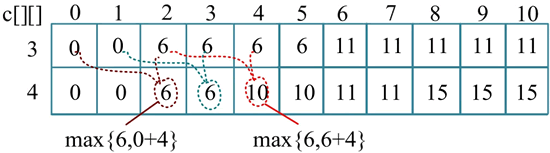
例如,处理到第 4 种物品(w[4]=2,v[4]=4)时,只需第 3 种物品的处理结果(上一行)。求第 j 列时,若 j<w[4],则照抄上一行;若 j≥w[4],则将上一行第 j 列的值与上一行第 j-w[4] 列的值 +v[4]的值进行比较,取最大值,如下图所示。
既然只需上一行当前列和前面列的值,则只用一个一维数组倒推就可以了:
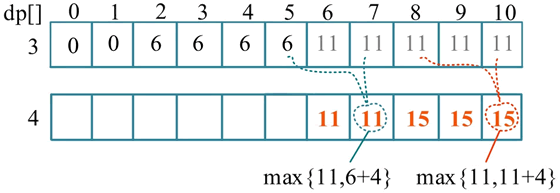
例如,处理到第 4 种物品(w[4]=2,v[4]=4)时,倒推的计算过程如下图所示。
为什么不正推呢?下面进行推理。
正推的情况:
第 i 阶段表示在处理第 i 种物品时,前 i-1 种物品已被处理完毕。倒推时,从后往前推,前面的值还未更新,仍为第 i-1 阶段的结果,这意味着总是用第 i-1 阶段的结果更新第 i 阶段,即从第 i-1 阶段向第 i 阶段进行状态转移。第 i-1 阶段的结果不包括第 i 种物品,保证第 i 种物品最多只被装入背包 1 次,如下图所示。

正推时,从前向后推,前面的值已被更新为第 i 阶段,这意味着用第 i 阶段的结果更新第 i 阶段,即从第 i 阶段向第 i 阶段进行状态转移。第 i 种物品可能被装入背包多次,如下图所示。

在 01 背包问题中,因为每种物品只有一个且最多被装入 1 次,所以必须通过倒推求解。若每种物品有多个且可被装入多次(完全背包),则可通过正推求解。
算法代码:
假设第 i 阶段处理第 i 种物品,第 i-1 阶段处理第 i-1 种物品,则当处理第 i 种物品时,前 i-1 种物品已处理完毕,只需考虑第 i-1 阶段向第 i 阶段的转移。
用 c[i][j] 表示将前 i 种物品装入容量为 j 的背包可以获得的最大价值。第 i 种物品的处理状态包括以下两种:
- 不装入:装入背包的物品的价值不增加,问题转换为“将前i-1种物品装入容量为j的背包获得的最大价值”,最大价值为 c[i-1][j]。
- 装入:在将第 i 种物品装入之前为第 i-1 阶段,相当于从第 i-1 阶段向第 i 阶段转换。问题转换为“将前 i-1 种物品装入容量为 j-w[i]的背包获得的最大价值”,此时获得的最大价值就是 c[i-1][j-w[i]],再加上装入第 i 种物品获得的价值 v[i],总价值为 c[i-1][j-w[i]]+v[i]。

若背包容量不足,则肯定不可以装入,价值仍为前 i-1 种物品处理后的结果;若背包容量充足,则考查装入不装入此物品哪种使得背包内的物品价值之和最大。
状态转移方程:
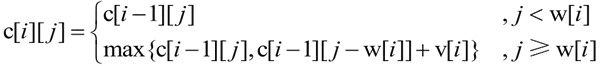
算法步骤
1) 初始化
初始化数组 c[][] 第 0 行第 0 列为 0:c[0][j]=0,c[i][0]=0,其中 i=0,1,2,…,n,j=0,1,2,…,W,表示装入第 0 种物品或背包容量为 0 时获得的价值均为 0。2) 循环阶段
- 按照状态转移方程处理第 1 种物品,得到 c[1][j],j=1,2,…,W。
- 按照状态转移方程处理第 2 种物品,得到 c[2][j],j=1,2,…,W。
- 以此类推,得到 c[n][j],j=1,2,…,W。
3) 构造最优解
c[n][W] 就是在不超过背包容量时可以装入物品的最大价值(最优值)。若还想知道具体装入了哪些物品,则需要根据数组 c[][] 逆向构造最优解。可以用一维数组 x[] 存储解向量,x[i]=1 表示第 i 种物品被装入背包,x[i]=0 表示第 i 种物品未被装入背包:
- 初始时 i=n,j=W。
- 若 c[i][j]>c[i-1][j],则说明第 i 种物品被装入背包,令 x[i]=1,j-=w[i];若 c[i][j]≤c[i-1][j],则说明第i种物品没被装入背包,令 x[i]=0。
- i--,转向第 2 步,直到 i=1 时处理完毕。
此时已经得到解向量(x[1],x[2],…,x[n]),直接输出该解向量,也可以仅输出 x[i]=1 的物品序号 i。
完美图解
有 5 种物品,重量分别为 2、5、4、2、3,价值分别为 6、3、5、4、6。背包容量为 10。求解在不超过背包容量的前提下将哪些物品装入背包,才可以使背包内的物品价值之和最大。
1) 初始化。c[i][j] 表示将前 i 种物品装入容量为 j 的背包可以获得的最大价值。初始化数组 c[][] 第 0 行第 0 列为 0。

2) 按照状态转移方程处理第 1 种物品(i=1),w[1]=2,v[1]=6,如下图所示。

其中:
- 当 j=1 时,c[1][1]=c[0][1]=0;
- 当 j=2 时,c[1][2]=max{c[0][2],c[0][0]+6}=6;
- 当 j=3 时,c[1][3]=max{c[0][3],c[0][1]+6}=6;
- 当 j=4 时,c[1][4]=max{c[0][4],c[0][2]+6}=6;
- 当 j=5 时,c[1][5]=max{c[0][5],c[0][3]+6}=6;
- 当 j=6 时,c[1][6]=max{c[0][6],c[0][4]+6}=6;
- 当 j=7 时,c[1][7]=max{c[0][7],c[0][5]+6}=6;
- 当 j=8 时,c[1][8]=max{c[0][8],c[0][6]+6}=6;
- 当 j=9 时,c[1][9]=max{c[0][9],c[0][7]+6}=6;
- 当 j=10 时,c[1][10]=max{c[0][10],c[0][8]+6}=6。
3) 按照状态转移方程处理第 2 种物品(i=2),w[2]=5,v[2]=3,如下图所示。

其中:
- 当 j=1 时,c[2][1]=c[1][1]=0;
- 当 j=2 时,c[2][2]=c[1][2]=6;
- 当 j=3 时,c[2][3]=c[1][3]=6;
- 当 j=4 时,c[2][4]=c[1][4]=6;
- 当 j=5 时,c[2][5]=max{c[1][5],c[1][0]+3}=6;
- 当 j=6 时,c[2][6]=max{c[1][6],c[1][1]+3}=6;
- 当 j=7 时,c[2][7]=max{c[1][7],c[1][2]+3}=9;
- 当 j=8 时,c[2][8]=max{c[1][8],c[1][3]+3}=9;
- 当 j=9 时,c[2][9]=max{c[1][9],c[1][4]+3}=9;
- 当 j=10 时,c[1][10]=max{c[1][10],c[1][5]+3}=9。
4) 按照状态转移方程处理第 3 种物品(i=3),w[3]=4,v[3]=5,如下图所示。

其中:
- 当 j=1 时,c[3][1]=c[2][1]=0;
- 当 j=2 时,c[3][2]=c[2][2]=6;
- 当 j=3 时,c[3][3]=c[2][3]=6;
- 当 j=4 时,c[3][4]=max{c[2][4],c[2][0]+5}=6;
- 当 j=5 时,c[3][5]=max{c[2][5],c[2][1]+5}=6;
- 当 j=6 时,c[3][6]=max{c[2][6],c[2][2]+5}=11;
- 当 j=7 时,c[3][7]=max{c[2][7],c[2][3]+5}=11;
- 当 j=8 时,c[3][8]=max{c[2][8],c[2][4]+5}=11;
- 当 j=9 时,c[3][9]=max{c[2][9],c[2][5]+5}=11;
- 当 j=10 时,c[3][10]=max{c[2][10],c[2][6]+5}=11。
5) 按照状态转移方程处理第 4 种物品(i=4),w[4]=2,v[4]=4,如下图所示。

其中:
- 当 j=1 时,c[4][1]=c[3][1]=0;
- 当 j=2 时,c[4][2]=max{c[3][2],c[3][0]+4}=6;
- 当 j=3 时,c[4][3]=max{c[3][3],c[3][1]+4}=6;
- 当 j=4 时,c[4][4]=max{c[3][4],c[3][2]+4}=10;
- 当 j=5 时,c[4][5]=max{c[3][5],c[3][3]+4}=10;
- 当 j=6 时,c[4][6]=max{c[3][6],c[3][4]+4}=11;
- 当 j=7 时,c[4][7]=max{c[3][7],c[3][5]+4}=11;
- 当 j=8 时,c[4][8]=max{c[3][8],c[3][6]+4}=15;
- 当 j=9 时,c[4][9]=max{c[3][9],c[3][7]+4}=15;
- 当 j=10 时,c[4][10]=max{c[3][10],c[3][8]+4}=15。
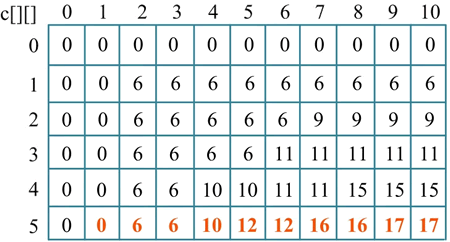
6) 按照状态转移方程处理第 5 种物品(i=5),w[5]=3,v[5]=6,如下图所示。

其中:
- 当 j=1 时,c[5][1]=c[4][1]=0;
- 当 j=2 时,c[5][2]=c[4][2]=6;
- 当 j=3 时,c[5][3]=max{c[4][3],c[4][0]+6}=6;
- 当 j=4 时,c[5][4]=max{c[4][4],c[4][1]+6}=10;
- 当 j=5 时,c[5][5]=max{c[4][5],c[4][2]+6}=12;
- 当 j=6 时,c[5][6]=max{c[4][6],c[4][3]+6}=12;
- 当 j=7 时,c[5][7]=max{c[4][7],c[4][4]+6}=16;
- 当 j=8 时,c[5][8]=max{c[4][8],c[4][5]+6}=16;
- 当 j=9 时,c[5][9]=max{c[4][9],c[4][6]+6}=17;
- 当 j=10 时,c[5][10]=max{c[4][10],c[4][7]+6}=17。
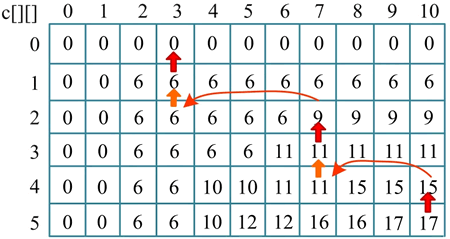
7) 构造最优解:
- ① 读取 c[5][10]>c[4][10],说明第 5 种物品被装入背包,即 x[5]=1,j=10-w[5]=7;
- ② 读取 c[4][7]=c[3][7],说明第 4 种物品没被装入背包,即 x[4]=0;
- ③ 读取 c[3][7]>c[2][7],说明第 3 种物品被装入背包,即 x[3]=1,j=j-w[3]=3;
- ④ 读取 c[2][3]=c[1][3],说明第 2 种物品没被装入背包,即 x[2]=0;
- ⑤ 读取 c[1][3]>c[0][3],说明第 1 种物品被装入背包,即 x[1]=1,j=j-w[1]=1,如下图所示。

算法实现
1) 求解装入背包的物品的最大价值
c[i][j] 表示将前 i 种物品装入容量为 j 的背包可以获得的最大价值。对每种物品都进行计算,背包容量 j 为 1~W:- 若物品重量大于背包容量,则不装入此物品,c[i][j]=c[i-1][j];
- 否则比较装入与不装入此物品哪种使得背包内的物品价值之和最大,即 c[i][j]=max(c[i-1][j], c[i-1][j-w[i]]+v[i])。
算法代码:
for(int i=1;i<=n;i++) //计算 c[i][j] for(int j=1;j<=W;j++) if(j<w[i]) //若物品的重量大于背包容量,则不装入此物品 c[i][j]=c[i-1][j]; else //否则比较装入与不装入此物品哪种使得背包内的物品价值之和最大 c[i][j]=max(c[i-1][j],c[i-1][j-w[i]]+v[i]); cout<<"装入背包的最大价值为:"<<c[n][W]<<endl;
2) 最优解构造
根据数组 c[][] 的计算结果逆向递推最优解,若 c[i][j]>c[i-1][j],则说明第 i 种物品被装入背包,令 x[i]=1,j-=w[i];若 c[i][j]≤c[i-1][j],则说明第 i 种物品没被装入背包,令 x[i]=0。算法代码:
int j=W; //逆向构造最优解
for(int i=n;i>0;i--) {
if(c[i][j]>c[i-1][j]) {
x[i]=1;
j-=w[i];
}
else
x[i]=0;
}
cout<<"装入背包的物品序号为:";
for(int i=1;i<=n;i++)
if(x[i]==1)
cout<<i<<" ";
本算法使用了两层 for 循环,时间复杂度为 O(nW);使用了二维数组 c[n][W],空间复杂度为 O(nW)。算法优化
根据求解过程可以看出,依次处理 1..n 的物品,当处理第 i 种物品时,只需第 i-1 种物品的处理结果,若不需要构造最优解,则装入第 i-1 种物品之前的处理结果已经没用了。例如,处理到第 4 种物品(w[4]=2,v[4]=4)时,只需第 3 种物品的处理结果(上一行)。求第 j 列时,若 j<w[4],则照抄上一行;若 j≥w[4],则将上一行第 j 列的值与上一行第 j-w[4] 列的值 +v[4]的值进行比较,取最大值,如下图所示。

既然只需上一行当前列和前面列的值,则只用一个一维数组倒推就可以了:
- 状态表示:dp[j] 表示将物品装入容量为 j 的背包可以获得的最大价值。
- 状态转移方程:dp[j]=max{dp[j],dp[j-w[i]]+v[i]}。
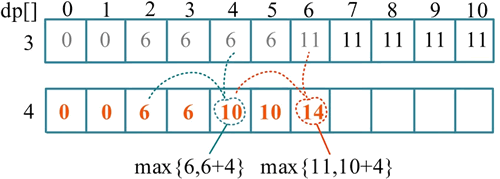
例如,处理到第 4 种物品(w[4]=2,v[4]=4)时,倒推的计算过程如下图所示。
- dp[10]=max(dp[10],dp[8]+4)=max(11,15)=15;
- dp[9]=max(dp[9],dp[7]+4)=max(11,15)=15;
- dp[8]=max(dp[8],dp[6]+4)=max(11,15)=15;
- dp[7]=max(dp[7],dp[5]+4)=max(11,10)=11;
- dp[6]=max(dp[6],dp[4]+4)=max(11,10)=11。

为什么不正推呢?下面进行推理。
正推的情况:
- 求解 dp[4] 时,将当前值与 dp[2]+4 进行比较,取最大值,发现将第 4 种物品装入后背包内的物品价值之和最大,结果为 10;
- 求解 dp[6] 时,将当前值与 dp[4]+4 进行比较,求最大值,发现将第 4 种物品装入后背包内的物品价值之和最大,结果为 14;
- 此时第 4 种物品被装入两次,因为在计算 dp[6] 时,dp[4] 不是第 3 种物品处理完毕的结果,而是装入第 4 种物品更新后的结果,如下图所示。

第 i 阶段表示在处理第 i 种物品时,前 i-1 种物品已被处理完毕。倒推时,从后往前推,前面的值还未更新,仍为第 i-1 阶段的结果,这意味着总是用第 i-1 阶段的结果更新第 i 阶段,即从第 i-1 阶段向第 i 阶段进行状态转移。第 i-1 阶段的结果不包括第 i 种物品,保证第 i 种物品最多只被装入背包 1 次,如下图所示。

正推时,从前向后推,前面的值已被更新为第 i 阶段,这意味着用第 i 阶段的结果更新第 i 阶段,即从第 i 阶段向第 i 阶段进行状态转移。第 i 种物品可能被装入背包多次,如下图所示。

在 01 背包问题中,因为每种物品只有一个且最多被装入 1 次,所以必须通过倒推求解。若每种物品有多个且可被装入多次(完全背包),则可通过正推求解。
算法代码:
void opt2(int n,int W) { // 01 背包问题,一维数组优化
for(i=1;i<=n;i++)
for(j=W;j>=w[i];j--) //逆序循环(倒推)
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
本算法包含两层 for 循环,时间复杂度为 O(nW);使用了一维数组 dp[W],空间复杂度为 O(W)。 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: