分治法求x的n次幂(Java实现)
求 x 的 n 次幂,可以利用简单的迭代法实现,也可将 x^n 看成是一个规模为 n 的 x 相乘问题,这样就可以将规模不断进行划分,直到规模为 1 为止。
求 x 的 n 次幂问题可分为两种情况:
根据以上分析,求 x 的 n 次幂问题可表示成以下递归模型:
当 n=1 时,如果程序要找全部解,在将找到的解输出后,应继续调整最后位置上填放的整数,试图找下一个解。相应的算法如下:
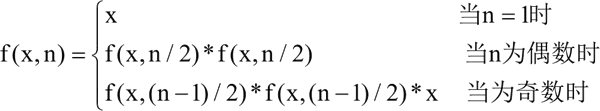
算法实现如下:
求 x 的 n 次幂问题可分为两种情况:
- xn = x(n/2)*x(n/2) (n是偶数)
- xn = x((n-1)/2)*x((n-1)/2)*x (n是奇数)
根据以上分析,求 x 的 n 次幂问题可表示成以下递归模型:
当 n=1 时,如果程序要找全部解,在将找到的解输出后,应继续调整最后位置上填放的整数,试图找下一个解。相应的算法如下:
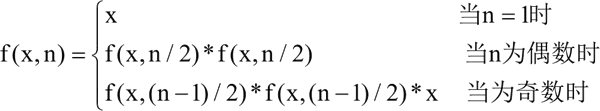
算法实现如下:
import java.util.Scanner;
public class ComputePow {
float Divide_Pow ( float x, float n ) {
float a;
if ( n == 1 )
return x;
else if ( (int)n % 2 == 0 ) // n 为偶数
{
a = Divide_Pow(x,n/2);
return a*a;
}
else // n 为奇数
{
a = Divide_Pow(x,(n-1)/2);
return a*a*x;
}
}
float Common_Pow ( float x, float y ) {
float result = 1.0f;
for ( int i = 1; i <= y; ++i )
{
result *= x;
}
return result;
}
public static void main(String args[])
{
float x; // 底数
float n; // 幂
System.out.print("请输入底数: ");
Scanner sc=new Scanner(System.in);
x=sc.nextFloat();
System.out.print("请输入幂: ");
n=sc.nextFloat();
ComputePow CP=new ComputePow();
System.out.println("普通的迭代法: "+x+"^"+n+"="+CP.Common_Pow(x,n));
System.out.println("分治法: "+x+"^"+n+"="+CP.Divide_Pow(x,n));
}
}
程序运行结果如下:
请输入底数:2 请输入幂:10 普通的迭代法:2.0^10.0=1024.0 分治法:2.0^10.0=1024.0在利用分治法实现时:
- 当 n=1 时,即幂为 1,其结果就是 x。
- 当 n 为偶数时,即幂为偶数,调用自身求 divide_pow(x,n/2)*divide_pow(x,n/2)。
- 当 n 为奇数时,即幂为奇数,调用自身求 divide_pow(x,(n-1)/2)*divide_pow(x,(n-1)/2)*x。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: