主成分分析法详解(附带实例,Python实现)
主成分分析(PCA)是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分。
PCA 用于去除噪声和不重要的特征时,将多个指标转换为少数几个主成分,这些主成分是原始变量的线性组合,且彼此之间互不相关,其能反映出原始数据的大部分信息,而且可以提升数据处理的速度。
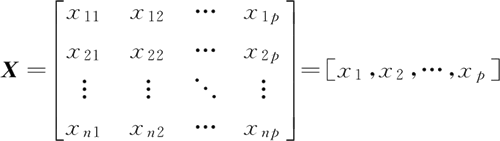
首先假设有 n 个样本,p 个特征,xij 表示第 i 个样本的第 j 个特征,这些样本构成的 n×p 特征矩阵 X 为:
目的是找到一个转换矩阵,将 p 个特征转化为 m 个特征(m<p),从而实现特征降维。即找到一组新的特征/变量 z1,z2,…,zm(m≤p),满足以下式子:
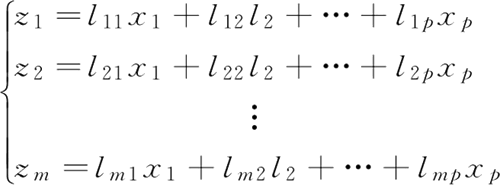
1) 计算每个特征(共p个特征)的均值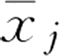 和标准差 Sj,公式为:
和标准差 Sj,公式为:
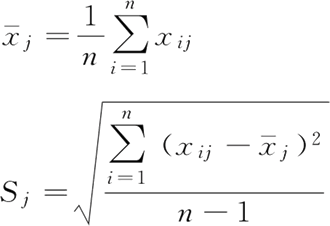
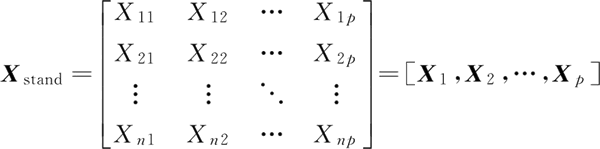
2) 将每个样本的每个特征进行标准化处理,得到标准化特征矩阵 Xstand:
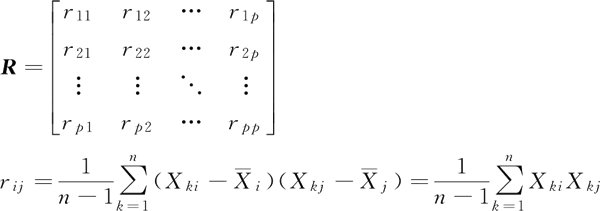
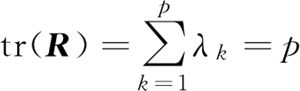
特征值:λ1≥λ2≥…≥λp≥0。
特征向量:
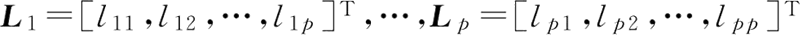
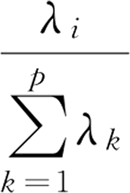
前 i 个主成分的累计贡献率为:
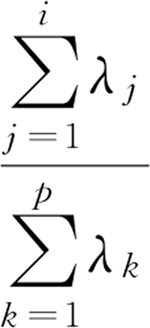
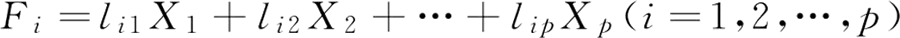
对于某个主成分而言,指示前面的系数(lij)越大,代表该指标对于该主成分的影响越大。
【实例】 利用 sklearn 包自带的 PCA 方法对 iris 数据集进行分析。iris(鸢尾花)数据集是常用的分类实验数据集,由 Fisher 在 1936 年收集整理。数据集包含 150 个数据,分为 3 类,每类 50 个数据,每个数据包含 4 个属性。可通过花萼长度、花萼宽度、花瓣长度、花瓣宽度 4 个属性预测鸢尾花卉属于(Setosa、Versicolour、Virginica)三类中的哪一类。
算法的具体步骤如下:
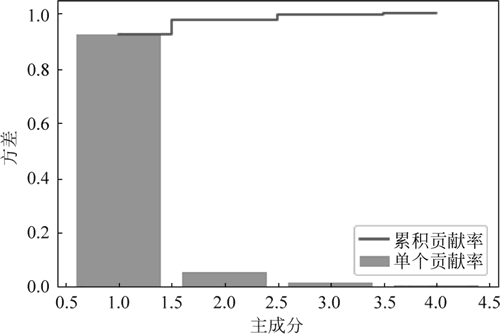
图 12 各特征值的贡献率
PCA 用于去除噪声和不重要的特征时,将多个指标转换为少数几个主成分,这些主成分是原始变量的线性组合,且彼此之间互不相关,其能反映出原始数据的大部分信息,而且可以提升数据处理的速度。
首先假设有 n 个样本,p 个特征,xij 表示第 i 个样本的第 j 个特征,这些样本构成的 n×p 特征矩阵 X 为:

目的是找到一个转换矩阵,将 p 个特征转化为 m 个特征(m<p),从而实现特征降维。即找到一组新的特征/变量 z1,z2,…,zm(m≤p),满足以下式子:
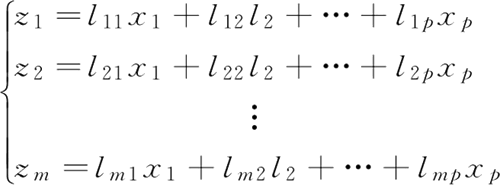
标准化
标准化过程如下:1) 计算每个特征(共p个特征)的均值
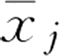 和标准差 Sj,公式为:
和标准差 Sj,公式为: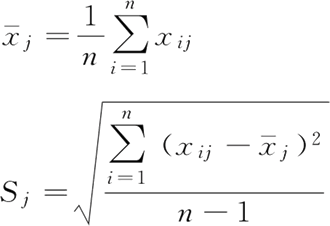
2) 将每个样本的每个特征进行标准化处理,得到标准化特征矩阵 Xstand:

协方差矩阵
协方差矩阵是汇总了所有可能配对的变量间相关性的一个表。协方差矩阵 R 为: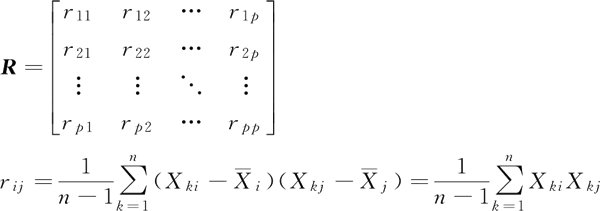
特征值和特征向量
计算矩阵 R 的特征值,并按照大小顺序排列,计算对应的特征向量,并进行标准化,使其长度为 1。R 是半正定矩阵,且: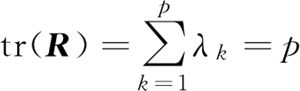
特征值:λ1≥λ2≥…≥λp≥0。
特征向量:
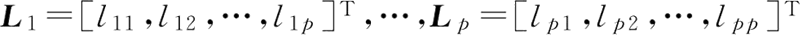
主成分贡献率与累计贡献率
第 i 个主成分的贡献率为: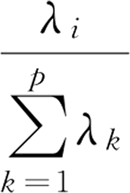
前 i 个主成分的累计贡献率为:
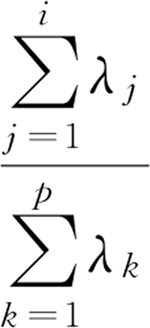
选取和表示主成分
一般累计贡献率超过80%的特征值所对应的第 1,2,…,m(m≤p)个主成分。Fi 表示第 i 个主成分: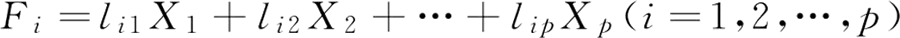
对于某个主成分而言,指示前面的系数(lij)越大,代表该指标对于该主成分的影响越大。
主成分分析实战
前面已对主成分分析的定义、标准化、协方差、特征值与特征向量、贡献率等内容进行了介绍,下面直接通过实例演示主成分分析实战。【实例】 利用 sklearn 包自带的 PCA 方法对 iris 数据集进行分析。iris(鸢尾花)数据集是常用的分类实验数据集,由 Fisher 在 1936 年收集整理。数据集包含 150 个数据,分为 3 类,每类 50 个数据,每个数据包含 4 个属性。可通过花萼长度、花萼宽度、花瓣长度、花瓣宽度 4 个属性预测鸢尾花卉属于(Setosa、Versicolour、Virginica)三类中的哪一类。
算法的具体步骤如下:
- 对向量 X 进行去中心化;
- 计算向量 X 的协方差矩阵,自由度可以选择 0 或者 1;
- 计算协方差矩阵的特征值和特征向量;
- 选取最大的 k 个特征值及其特征向量;
- 用 X 与特征向量相乘。
import numpy as np
from numpy.linalg import eig
from sklearn.datasets import load_iris
def pca(X,k):
X = X-X.mean(axis = 0) #向量X去中心化
X_cov = np.cov(X.T,ddof = 0) #计算向量X的协方差矩阵,自由度可以选择0或1
eigenvalues,eigenvectors = eig(X_cov) #计算协方差矩阵的特征值和特征向量
klarge_index = eigenvalues.argsort()[-k:][::-1] #选取最大的k个特征值及其特征向量
k_eigenvectors = eigenvectors[klarge_index] #用X与特征向量相乘
return np.dot(X,k_eigenvectors.T)
iris = load_iris()
X = iris.data
k = 2
X_pca = pca(X,k)
print(X_pca)
[[ 4.91948928e-01 -1.34738775e + 00]
[ 7.47900934e-01 -9.66077783e-01]
[ 6.02374750e-01 -1.15520829e + 00]
[ 5.15670315e-01 -9.54726544e-01]
[ 3.90135972e-01 -1.41213209e + 00]
...
[ 3.01389471e-02 8.79746675e-01]
[ -3.10287060e-01 5.85310893e-01]
[ -7.02403009e-01 3.40161924e-01]
[ -5.32592048e-01 6.39849289e-01]]
'''查年各特征值的贡献率'''
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from numpy.linalg import eig
#matplotlib inline
plt.rcParams['font.sans-serif'] = ['SimHei'] #显示中文
iris = load_iris()
X = iris.data
X = X-X.mean(axis = 0)
#计算协方差矩阵
X_cov = np.cov(X.T,ddof = 0)
#计算协方差矩阵的特征值和特征向量
eigenvalues,eigenvectors = eig(X_cov)
tot = sum(eigenvalues)
var_exp = [(i/tot)for i in sorted(eigenvalues,reverse = True)]
cum_var_exp = np.cumsum(var_exp)
plt.bar(range(1,5),var_exp,alpha = 0.5,align = 'center',label = '单个贡献率')
plt.step(range(1,5),cum_var_exp,where = 'mid',label = '累积贡献率')
plt.ylabel('方差')
plt.xlabel('主成分')
plt.legend(loc = 'best')
plt.show()
运行程序,效果如下图所示。
图 12 各特征值的贡献率
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: