主成分分析是什么,PyTorch实现主成分分析(附带实例)
主成分分析(Principal Component Analysis,PCA)是一个线性变换,它把数据变换到一个新的坐标系统中,使得任何数据投影的第一大方差在第一主成分上,第二大方差在第二主成分上,以此类推。
本节重点介绍如何在 PyTorch 中实现主成分分析及其建模案例。
在用统计方法研究多变量问题时,变量太多会增加计算量和分析问题的复杂性,人们希望在进行定量分析的过程中,涉及的变量较少,得到的信息量较多。主成分分析正是适应这一要求产生的,是解决这类问题的理想工具。
主成分分析常用于降低数据集的维度,其目标是保留对数据方差贡献最大的特征。这是通过保留低阶的主成分,忽略高阶的主成分做到的。这样低阶成分往往能够保留数据最重要的方面。
例如,在对科普书籍开发和利用这一问题的评估中,涉及科普创作人数、科普作品发行量、科普产业化(科普示范基地数)等多项指标。经过对数据进行主成分分析,最后确定几个主成分作为综合评价科普书籍利用和开发的综合指标,变量数减少,并达到一定的可信度,就容易进行科普效果的评估。
主成分分析的思想是将原来众多具有一定相关性的变量,重新组合成一组新的互相无关的综合指标来代替原来的指标。它借助一个正交变换,将其分量相关的原随机向量转换成其分量不相关的新随机向量,这在代数上表现为将原随机向量的协方差阵变换成对角形阵,在几何上表现为将原坐标系变换成新的正交坐标系,使之指向样本点散布最开的 p 个正交方向,然后对多维变量系统进行降维处理。方差较大的几个新变量就能综合反映原来多个变量所包含的主要信息,并且也包含自身特殊的含义。
主成分分析的数学模型为:
主成分分析的建模步骤如下:
1) 对原有变量进行坐标变换,可得:
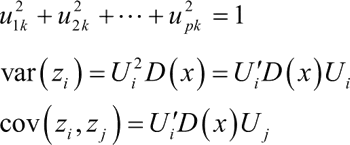
2) 提取主成分:
z1 称为第一主成分,满足条件如下:
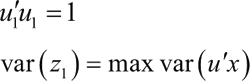
z2 称为第二主成分,满足条件如下:
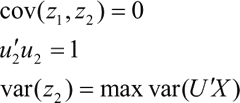
其余主成分以此类推。
本例的原始数据如下表所示:
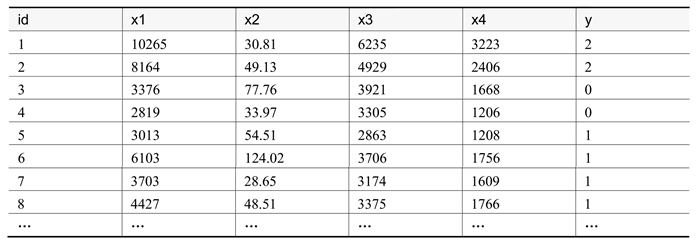
操作步骤如下:
1) 导入相关库,代码如下:
2) 读取数据,代码如下:
3) 变量特征降维,代码如下:
4) 设置网络结构,代码如下:
在代码中,使用 torch.nn.Sequential 来按顺序堆叠神经网络的各个层。每个层都是通过 torch.nn.Linear 来定义线性变换的,其中第一个线性层将输入的维度从 2 变换到 10,第二个线性层将输入的维度从 10 变换到 3。
在每个线性层之后,使用了 torch.nn.ReLU 激活函数来引入非线性层。最后,通过 print(net) 打印出神经网络的结构,以便查看网络的层和连接方式。
这样的神经网络结构可以用于多种任务,例如分类、回归等。具体的应用和训练过程取决于数据和任务的要求。在实际应用中,还需要进行数据加载、损失函数定义、优化器选择和训练循环等步骤来训练和使用这个神经网络。
5) 设置优化器,随机梯度下降,代码如下:
在训练神经网络时,优化器用于根据损失函数的反馈来更新网络的参数,以最小化损失。损失函数则用于衡量模型预测结果与真实标签之间的差异。
具体的应用场景和使用方式会根据神经网络的结构和任务的需求而有所不同。在训练过程中,通常会使用优化器和损失函数来进行反向传播和参数更新,以不断改进模型的性能。
6) 训练模型,并进行可视化,代码如下:
代码使用循环进行多次迭代。在每次迭代中,通过网络进行前向传播计算输出,并使用损失函数计算损失。然后,清空梯度并进行反向传播以计算梯度,最后根据梯度更新参数。
每隔 25 次迭代,会进行以下操作:
这样的代码结构通常用于训练神经网络,并在训练过程中定期查看模型的预测结果和准确率。通过可视化,可以观察模型在数据上的表现,并根据准确率来评估模型的性能。具体的应用场景和调整方式会根据任务和数据的特点而有所不同。
7) 保存网络及其参数,代码如下:
这些保存操作通常用于模型的持久化,以便在后续的运行中可以加载和使用已经训练好的模型。保存模型和参数可以方便地在不同的程序或环境中复用模型。
请确保在运行代码时,指定的文件路径'./主成分分析/'存在并且可写,否则可能会导致保存失败。另外,加载保存的模型和参数时,需要使用相应的 torch.load 函数来读取文件并还原模型。
输出的网络结构如下:
Sequential 模型是 PyTorch 中一种常见的模型结构,其中的各层按照顺序堆叠在一起。每层都由一个元组表示,元组中的第一个元素是层的类型,后面的元素可能是层的参数。
在这个例子中,通过 Sequential 定义了一个简单的前馈神经网络,它包含两个线性变换层和一个激活函数。这样的结构可以用于各种任务,例如分类、回归等。具体的应用和效果将取决于数据、训练方法以及其他因素。在实际应用中,可能还需要进一步调整网络结构、超参数和训练过程,以获得更好的性能。
当准确率为 0.17 时,如下图所示:
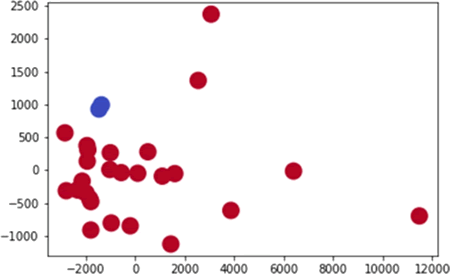
图 5 准确率为 0.17
当准确率为 0.48 时,如下图所示:
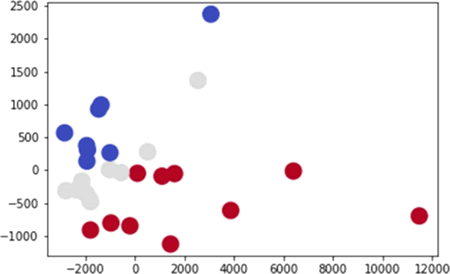
图 6 准确率为 0.48
当准确率为 0.62 时,如下图所示:
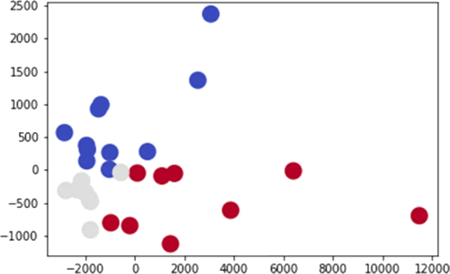
图 7 准确率为 0.62
当准确率为 0.69 时,如下图所示:
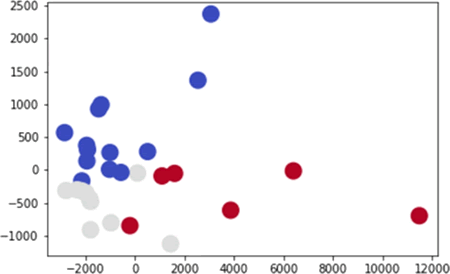
图 8 准确率为 0.69
本节重点介绍如何在 PyTorch 中实现主成分分析及其建模案例。
主成分分析是什么
在统计分析中,为了全面、系统地分析问题,我们必须考虑众多影响因素。这些涉及的因素一般称为指标,在多元统计分析中也称为变量。因为每个变量都在不同程度上反映了所研究问题的某些信息,并且指标之间彼此有一定的相关性,因而所得的统计数据反映的信息在一定程度上有重叠。在用统计方法研究多变量问题时,变量太多会增加计算量和分析问题的复杂性,人们希望在进行定量分析的过程中,涉及的变量较少,得到的信息量较多。主成分分析正是适应这一要求产生的,是解决这类问题的理想工具。
主成分分析常用于降低数据集的维度,其目标是保留对数据方差贡献最大的特征。这是通过保留低阶的主成分,忽略高阶的主成分做到的。这样低阶成分往往能够保留数据最重要的方面。
例如,在对科普书籍开发和利用这一问题的评估中,涉及科普创作人数、科普作品发行量、科普产业化(科普示范基地数)等多项指标。经过对数据进行主成分分析,最后确定几个主成分作为综合评价科普书籍利用和开发的综合指标,变量数减少,并达到一定的可信度,就容易进行科普效果的评估。
主成分分析建模
主成分分析是将多个变量通过线性变换以选出较少重要变量的一种多元统计分析方法。主成分分析的思想是将原来众多具有一定相关性的变量,重新组合成一组新的互相无关的综合指标来代替原来的指标。它借助一个正交变换,将其分量相关的原随机向量转换成其分量不相关的新随机向量,这在代数上表现为将原随机向量的协方差阵变换成对角形阵,在几何上表现为将原坐标系变换成新的正交坐标系,使之指向样本点散布最开的 p 个正交方向,然后对多维变量系统进行降维处理。方差较大的几个新变量就能综合反映原来多个变量所包含的主要信息,并且也包含自身特殊的含义。
主成分分析的数学模型为:
z1=u11X1+u12X2+…+u1pXp
z2=u21X1+u22X2+…+u2pXp
…
zp=up1X1+up2X2+…+uppXp
主成分分析的建模步骤如下:
1) 对原有变量进行坐标变换,可得:
z1=u11x1+u21x2+…+up1xp
z2=u12x1+u22x2+…+up2xp
…
zp=u1px1+u2px2+…+uppxp
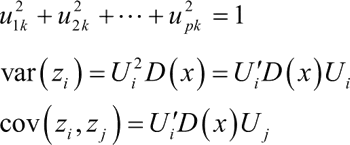
2) 提取主成分:
z1 称为第一主成分,满足条件如下:
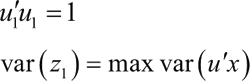
z2 称为第二主成分,满足条件如下:
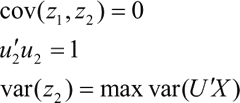
其余主成分以此类推。
地区竞争力指标降维
衡量我国各省市综合发展情况的一些数据,数据来源于《中国统计年鉴》。数据表中选取了 6 个指标,分别是人均 GDP、固定资产投资、社会消费品零售总额、农村人均纯收入等,下面将利用因子分析来提取公共因子,分析衡量发展因素的指标。本例的原始数据如下表所示:
表:地区竞争力数据

操作步骤如下:
1) 导入相关库,代码如下:
#导入相关库 import torch import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn.decomposition import PCA from torch.autograd import Variable import torch.nn.functional as F
2) 读取数据,代码如下:
# 读取文件并将数据存储在 DataFrame 中
region = pd.read_csv("./主成分分析/region.csv")
# 从 region 数据框中选择'x1'、'x2'、'x3'和'x4'列
region_d = region[['x1', 'x2', 'x3', 'x4']]
# 将 region 数据框中的'y'列数据赋值给'target'列
region['target'] = region['y']
这段代码用于数据处理和分析,根据具体的需求选择特定的列,并进行数据的重新组织或修改。请根据实际情况和数据的特点来理解和使用这些代码片段。3) 变量特征降维,代码如下:
# 创建一个主成分分析(PCA)对象,指定保留的主成分数量为 2 transfer_1 = PCA(n_components=2) # 使用拟合和转换方法对 region_d 进行主成分分析 region_d = transfer_1.fit_transform(region_d) # 将 region_d 转换为 Torch 中的 NumPy 数组 x = torch.from_numpy(region_d) # 将 region 中的 'target' 列转换为 Torch 中的 NumPy 数组 y = torch.from_numpy(np.array(region['target'])) # 将 x 和 y 转换为 Variable 对象 x, y = Variable(x), Variable(y)这段代码用于将数据转换为适合特定深度学习框架(如 Torch)使用的格式,并为进一步的处理和分析做好准备。具体的应用场景和后续操作将取决于整体的项目需求和数据处理流程。
4) 设置网络结构,代码如下:
# 使用 torch.nn.Sequential 构建神经网络
net = torch.nn.Sequential(
# 第一个线性层,输入维度为 2,输出维度为10
torch.nn.Linear(2, 10),
# ReLU 激活函数
torch.nn.ReLU(),
# 第二个线性层,输入维度为 10,输出维度为3
torch.nn.Linear(10, 3),
)
# 打印神经网络结构
print(net)
这段代码定义了一个简单的神经网络结构,并打印出该神经网络。在代码中,使用 torch.nn.Sequential 来按顺序堆叠神经网络的各个层。每个层都是通过 torch.nn.Linear 来定义线性变换的,其中第一个线性层将输入的维度从 2 变换到 10,第二个线性层将输入的维度从 10 变换到 3。
在每个线性层之后,使用了 torch.nn.ReLU 激活函数来引入非线性层。最后,通过 print(net) 打印出神经网络的结构,以便查看网络的层和连接方式。
这样的神经网络结构可以用于多种任务,例如分类、回归等。具体的应用和训练过程取决于数据和任务的要求。在实际应用中,还需要进行数据加载、损失函数定义、优化器选择和训练循环等步骤来训练和使用这个神经网络。
5) 设置优化器,随机梯度下降,代码如下:
# 定义优化器,优化器使用随机梯度下降 (SGD),学习率为 0.00001 optimizer = torch.optim.SGD(net.parameters(), lr=0.00001) # 定义损失函数 loss_func = torch.nn.CrossEntropyLoss() # 损失函数使用交叉熵损失这段代码主要定义了神经网络的优化器和损失函数。
在训练神经网络时,优化器用于根据损失函数的反馈来更新网络的参数,以最小化损失。损失函数则用于衡量模型预测结果与真实标签之间的差异。
具体的应用场景和使用方式会根据神经网络的结构和任务的需求而有所不同。在训练过程中,通常会使用优化器和损失函数来进行反向传播和参数更新,以不断改进模型的性能。
6) 训练模型,并进行可视化,代码如下:
for t in range(100): # 遍历 100 次
# 前向传播,计算网络输出
out = net(x.float())
# 计算损失
loss = loss_func(out, y.long())
# 清空梯度
optimizer.zero_grad()
# 反向传播计算梯度
loss.backward()
# 根据梯度更新参数
optimizer.step()
if t % 25 == 0: # 每 25 次迭代
# 清空图形
plt.cla()
# 获取预测结果
prediction = torch.max(out, 1)[1]
# 将预测结果转换为 NumPy 数组
pred_y = prediction.data.numpy()
# 将真实标签转换为 NumPy 数组
target_y = y.data.numpy()
# 在图上绘制预测结果,颜色代表类别
plt.scatter(x.data.numpy()[:, 0],
x.data.numpy()[:, 1],
c=pred_y,
s=100,
lw=5,
cmap='coolwarm')
# 计算准确率
accuracy = float((pred_y == target_y).astype(int).sum()) / float(target_y.size)
# 打印准确率
print('Accuracy=%.2f' % accuracy)
# 暂停 0.1 秒显示图形
plt.pause(0.1)
# 显示最终图形
plt.show()
这段代码是一个神经网络的训练循环,包含前向传播、计算损失、反向传播、参数更新以及每隔一定步数进行的可视化和准确率计算。代码使用循环进行多次迭代。在每次迭代中,通过网络进行前向传播计算输出,并使用损失函数计算损失。然后,清空梯度并进行反向传播以计算梯度,最后根据梯度更新参数。
每隔 25 次迭代,会进行以下操作:
- 清空图形;
- 获取预测结果,并将其转换为NumPy数组;
- 获取真实标签,并将其转换为NumPy数组;
- 在图上绘制预测结果,根据预测结果的类别用不同颜色表示;
- 计算准确率并打印;
- 暂停 0.1 秒以显示图形;
- 显示图形。
这样的代码结构通常用于训练神经网络,并在训练过程中定期查看模型的预测结果和准确率。通过可视化,可以观察模型在数据上的表现,并根据准确率来评估模型的性能。具体的应用场景和调整方式会根据任务和数据的特点而有所不同。
7) 保存网络及其参数,代码如下:
# 将网络模型保存到文件'./主成分分析/net.pkl'中,这将保存网络的结构和参数 torch.save(net,'./主成分分析/net.pkl') # 将网络的状态字典保存到文件'./主成分分析/net_params.pkl'中,状态字典包含了网络的参数 torch.save(net.state_dict(),'./主成分分析/net_params.pkl')这段代码使用 torch.save 函数将网络模型和网络的状态字典分别保存到指定的文件中。
这些保存操作通常用于模型的持久化,以便在后续的运行中可以加载和使用已经训练好的模型。保存模型和参数可以方便地在不同的程序或环境中复用模型。
请确保在运行代码时,指定的文件路径'./主成分分析/'存在并且可写,否则可能会导致保存失败。另外,加载保存的模型和参数时,需要使用相应的 torch.load 函数来读取文件并还原模型。
输出的网络结构如下:
Sequential(
(0): Linear(in_features=2, out_features=10, bias=True) # 线性层,输入特征数为 2,
输出特征数为 10,启用偏置
(1): ReLU() # ReLU 激活函数
(2): Linear(in_features=10, out_features=3, bias=True) # 线性层,输入特征数为 10,输出特征数为 3,启用偏置
)
这段代码定义了一个 Sequential 模型,它由三层组成:
- 第一层是线性层(Linear),它将输入的特征数量从 2 变换到 10,并启用了偏置项(bias=True)。
- 第二层是 ReLU 激活函数,它用于引入非线性因素。
- 第三层也是线性层,它将特征数量从 10 变换到 3,同样启用了偏置项。
Sequential 模型是 PyTorch 中一种常见的模型结构,其中的各层按照顺序堆叠在一起。每层都由一个元组表示,元组中的第一个元素是层的类型,后面的元素可能是层的参数。
在这个例子中,通过 Sequential 定义了一个简单的前馈神经网络,它包含两个线性变换层和一个激活函数。这样的结构可以用于各种任务,例如分类、回归等。具体的应用和效果将取决于数据、训练方法以及其他因素。在实际应用中,可能还需要进一步调整网络结构、超参数和训练过程,以获得更好的性能。
当准确率为 0.17 时,如下图所示:

图 5 准确率为 0.17
当准确率为 0.48 时,如下图所示:

图 6 准确率为 0.48
当准确率为 0.62 时,如下图所示:

图 7 准确率为 0.62
当准确率为 0.69 时,如下图所示:

图 8 准确率为 0.69
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: