PCA主成分分析法(Python实现)
主成分分析,即 PCA,是一种常见的无监督学习算法,主要用于数据的降维和可视化。主成分分析通过找出数据中的主要成分,即解释数据方差最大的方向,从而达到简化数据复杂性的目的。
下面介绍 PCA 的工作原理。
1) PCA 计算数据集的协方差矩阵。
在统计和概率理论中,协方差矩阵是一个表示几个变量之间协方差的方阵。对于一个数据集,每个变量都有一定的方差,该方差表示该变量数据分散的程度。不同的变量之间也可能存在某种协方差,该协方差表示这两个变量可能以某种方式相关。
协方差矩阵的对角线上的元素是各个变量的方差,非对角线上的元素是对应两个变量的协方差。对于给定的 n 维数据集,其协方差矩阵将是一个 n×n 的矩阵。
例如,对于三个变量 X、Y 和 Z 的数据集,其协方差矩阵可能如下:
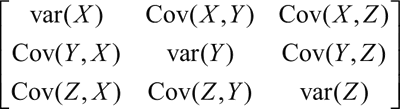
式中,var(X)、var(Y) 和 var(Z) 分别代表变量 X、Y 和 Z 的方差,Cov(X, Y)、Cov(X, Z) 和 Cov(Y, Z) 分别代表变量 X、Y 和 Z 之间的协方差。
2) PCA 找到这个协方差矩阵的特征值和特征向量。这些特征向量也被称为主成分,主成分就是我们要找的解释数据方差最大的方向。
3) PCA 按照特征值的大小对这些主成分进行排序,并选择前 k 个主成分。这样,用户就可以用这 k 个主成分代替原来的数据,从而达到降维的目的。
在 Python 中,用户可以使用 Scikit-Learn 库中的 PCA 类实现主成分分析。下面是一个简单的例子:
下面介绍 PCA 的工作原理。
1) PCA 计算数据集的协方差矩阵。
在统计和概率理论中,协方差矩阵是一个表示几个变量之间协方差的方阵。对于一个数据集,每个变量都有一定的方差,该方差表示该变量数据分散的程度。不同的变量之间也可能存在某种协方差,该协方差表示这两个变量可能以某种方式相关。
协方差矩阵的对角线上的元素是各个变量的方差,非对角线上的元素是对应两个变量的协方差。对于给定的 n 维数据集,其协方差矩阵将是一个 n×n 的矩阵。
例如,对于三个变量 X、Y 和 Z 的数据集,其协方差矩阵可能如下:
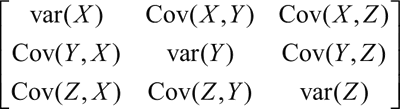
式中,var(X)、var(Y) 和 var(Z) 分别代表变量 X、Y 和 Z 的方差,Cov(X, Y)、Cov(X, Z) 和 Cov(Y, Z) 分别代表变量 X、Y 和 Z 之间的协方差。
2) PCA 找到这个协方差矩阵的特征值和特征向量。这些特征向量也被称为主成分,主成分就是我们要找的解释数据方差最大的方向。
3) PCA 按照特征值的大小对这些主成分进行排序,并选择前 k 个主成分。这样,用户就可以用这 k 个主成分代替原来的数据,从而达到降维的目的。
在 Python 中,用户可以使用 Scikit-Learn 库中的 PCA 类实现主成分分析。下面是一个简单的例子:
from sklearn.decomposition import PCA # 创建一个 PCA 实例,设定要保留的主成分数量为 2 pca = PCA(n_components=2) # 使用 PCA 对数据进行降维 X_pca = pca.fit_transform(X)
- pca=PCA(n_components=2):创建一个 PCA 对象。参数 n_components=2 表示用户希望将数据降维到两个主成分上。换句话说,用户想要通过 PCA 降低数据维度,保留数据中的两个主要成分;
- X_pca=pca.fit_transform(X):首先,对数据 X 进行拟合,找出 PCA 变换需要的参数;然后,使用这些参数对 X 进行变换,将原始数据映射到主成分定义的空间。X_pca 是转换后的数据,其每个数据点现在都是二维的,因为我们选择了两个主成分。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: