PCA降维算法详解
非监督学习算法从目的上来说主要有聚类和降维两大类,本节主要给大家介绍一个经典的非监督学习降维算法,叫做主成分分析(PCA)算法。
假设有 5 只猫,每只猫的毛色、体型、身高、体重、年龄、性别等特征各不相同。这里的猫就是对象,“猫”这个称呼是这个对象的标签,毛色、体型、体重等特征就是对象的属性。
在实际的图像识别过程中,可能有大量的猫、狗的图片,所需的对象的属性也有多个,这些属性的个数就是维度。维度越高,数据量越大,占用的磁盘空间和内存就越多。
但很多时候用不到这么多的信息,或者因为其他的一些原因,不能在太高的维度下进行操作,这时就需要进行数据降维。
具体来说,数据降维主要指的是按照一定的方法降低数据的特征维度,这样做的原因主要有三个:
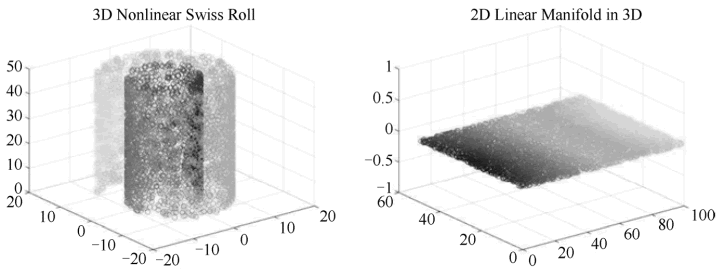
图 1 数据可视化效果图
综上所述,数据降维的意义如下:克服维度灾难,获取本质特征,节省存储空间,去除无用的噪声,实现数据可视化。
PCA 算法可以通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维数据的降维。这种算法和监督学习算法中的 Fisher 线性判别分析比较类似,都是将数据投影到一个可分性更好的投影空间,但 PCA 算法是一种非监督学习算法,不需要任何数据标签即可做到对数据进行变换投影。
PCA 算法通过找到一组线性变换的向量来对原始数据进行投影,那么如何衡量投影的优劣呢?
在数学上通常有两种方法衡量投影的优劣:
值得注意的是,这两种方法在数学上是完全等价的,下面就基于这两种方法来进行 PCA 算法的推导。
首先,考虑在一维空间(k=1)中的投影。可以使用 n 维向量 u 定义这个空间的方向。假定选择一个单位向量 u,使得 uTu=1。注意,这里只对 u 的方向感兴趣,而对 u 本身的大小不感兴趣。
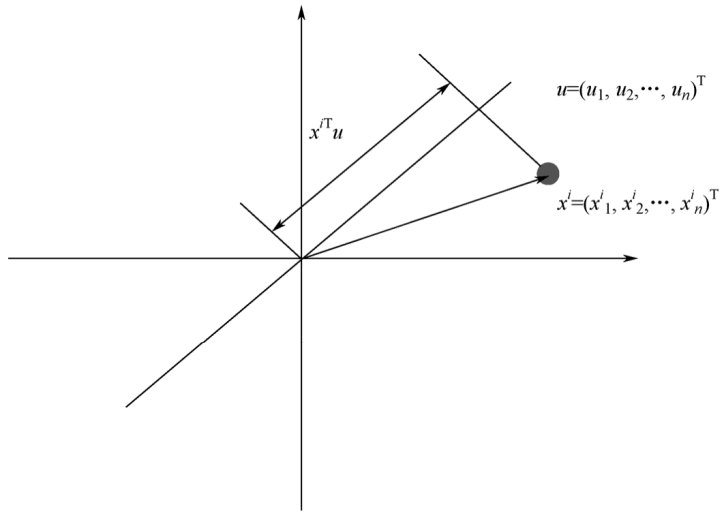
图 2 投影图
图 2 中的点表示原样本点 xi,u 是直线的斜率,也是直线的方向向量,而且是单位向量,直线上的点表示原样本点 xi 在 u 上的投影。由数据投影的基本原理知道,投影点与原点的距离是 xiᵀu,由于这些原始样本点的每一维特征均值都为 0,因此投影到 u 上的样本点的均值仍然是 0。
假设原始数据集为 X,目标是找到最佳的投影空间 w=(w1,w2,…,wk),其中 wi 是单位向量且 wi 与 wj(i≠j)正交。何为最佳的 w?就是原始样本点投影到 w 上之后,使得投影后的样本点方差最大。由于投影后均值为 0,因此投影后的总方差为:
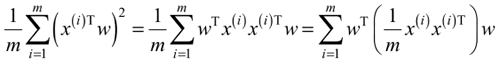
因为 x(i) 的均值为 0,所以等式右边小括号里的那部分其实就是原始数据集 X 的协方差矩阵(因为无偏估计的原因,一般协方差矩阵除以 m-1,这里用 m)。
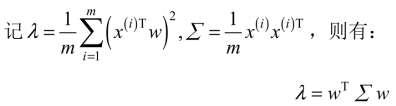
上式两边同时左乘 w,注意到 wwT=1(单位向量),则有:
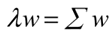
所以 w 其实是矩阵 ∑ 的特征值所对应的特征向量。欲使投影后的总方差最大,即λ最大,则最佳的投影向量 w 是特征值 λ 最大时对应的特征向量。因此,当将 w 设置为与具有最大的特征值 λ 的特征向量相等时,方差会达到最大值。这个特征向量被称为第一主成分。
可以用一种增量的方式定义额外的主成分,具体如下:在所有与那些已经考虑过的方向正交的所有可能的方向中,将新的方向选择为最大化投影方差的方向。如果考虑 k 维投影空间的一般情形,那么最大化投影数据方差的最优线性投影由数据协方差矩阵 ∑ 的 k 个特征向量 w₁,…,wk 定义,对应 k 个最大的特征值 λ₁,…,λk。
因此,只需要对协方差矩阵进行特征值分解,得到的前 k 大特征值对应的特征向量就是最佳的 k 维新特征,而且这 k 维新特征是正交的。得到前 k 个 u 以后,原始数据集 X 通过变换可以得到新的样本。
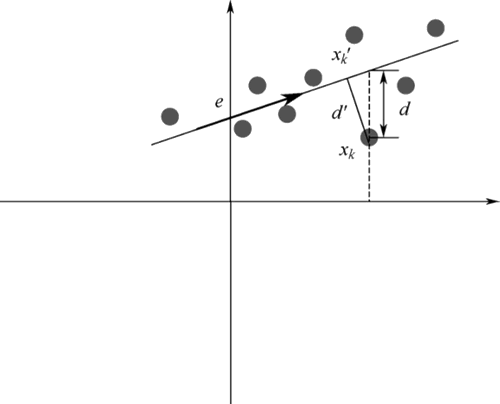
图 6 最小平方误差图
假设二维样本点如图 6 所示,按照前面讲解的最大方差理论,目标是求一条直线,使得样本点投影到直线上的点的方差最大。
从求解直线的思路出发,容易想到数学中的线性回归问题,其目标也是求解一个线性函数,使得对应直线能够更好地拟合样本点集合。如果从这个角度出发推导 PCA 算法,那么问题会转化为一个回归问题。回归时的最小二乘法度量的是样本点到直线的坐标轴距离。
比如这个问题中,特征是 x,类标签是 y。回归时最小二乘法度量的是距离 d。如果使用回归法来度量最佳直线,那么就是直接在原始样本上做回归。因此,可以选用另一种评价直线好坏的方法,即使用点到直线的距离 d′ 来度量。
现有 m 个样本点,每个样本点为 n 维。目标是最小化样本点与投影点之间的距离,称之为最小平方误差。
假设 xk 表示 p 维空间的 k 个点,zk 表示 xk 在超平面 D 上的投影向量,w=(w1,w2,…,wd)为 d 维空间的标准正交基,则最小平方误差理论可以转换为如下优化问题:
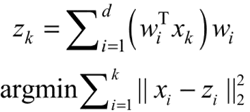
s.t.wiTwj=p(当 i=j 时 p=1,否则 p=0)
其中,wiTxk 为 xk 在 wi 基向量上的投影长度,wiTxkwi 为 wi 基向量的坐标值。
求解过程如下:
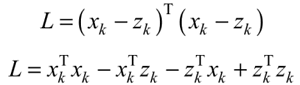
由于向量有内积性质 xTkzk=zTkxk ,可得:
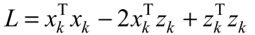
将 zk 的表达式代入得:
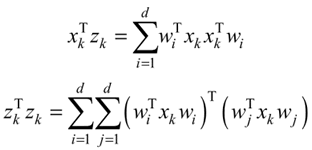
根据约束条件得:
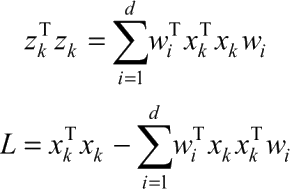
根据奇异值分解:
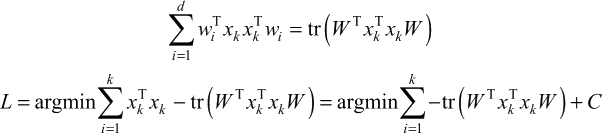
等价于带约束的优化问题:
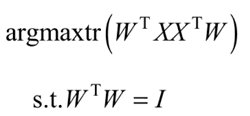
该问题的求解结果最佳超平面 W 与最大方差理论求解的最佳投影方向一致,即协方差矩阵的最大特征值所对应的特征向量,差别仅是协方差矩阵的一个倍数。
假设现在有 5 个 2 维数据 [-1,1]、[-2,-1]、[-3,-2]、[1,1]、[2,1] 组成的矩阵 X:
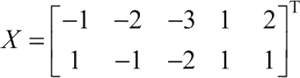
使用上述算法流程将这 5 个 2 维数据降维处理成 5 个 1 维数据,过程如下:
① 计算原始数据中每一列的均值为 [-0.6,0],将每一列数据减去均值,得到去中心化的结果 X₂ 如下:
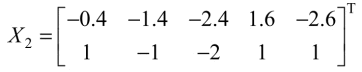
②求出矩阵 X₂ 的协方差矩阵为 Y=
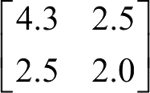
③ 求出协方差矩阵 Y 的特征值为 5.902 和 0.398,对应的特征向量组成的矩阵为:
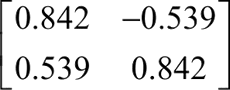
④ 将得到的特征向量依据特征值的大小按行排列成一个矩阵,组成矩阵 P=
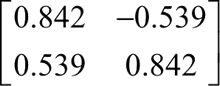
这里由于第一个特征值本来就大于第二个特征值,所以排序后得到的矩阵和步骤 ③ 中特征向量组成的初始矩阵一致。
⑤ 用矩阵 P 的第一列 P₁ 表示转换矩阵,令 Z=XP₁,得到的 1 维向量即降到 1 维的特征数据 Z=[0.2-1.7-3.0 1.9 2.7]ᵀ。
对该组数据进行降维处理的结果如下图所示:
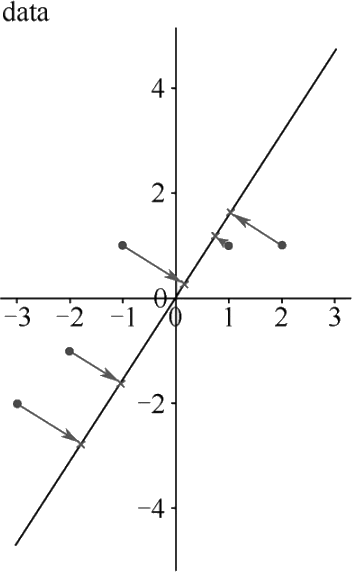
图 19 PCA算法结果示意图
这里需要注意一下特征数据的去中心化的问题。
所谓去中心化,就是将样本X中的每个观测值都减去样本均值,这样做的好处主要是能够使求解协方差矩阵变得更容易。
另外,为了简单起见,上述示例的特征数据维度并不高,可以直接进行矩阵分解计算。但是在真实的应用案例当中,特征数据的维度通常都很高,PCA 通常是数值近似分解,而非求特征值、奇异值得到解析解,所以当使用梯度下降法等算法进行PCA的时候,最好先对数据进行标准化,这有利于梯度下降法的收敛。

图 20 ORL数据库示例图像
ORL 数据库中的每张图片大小是 92×112 像素,转换成特征向量共有 10304 维。如果直接使用这个维度来进行识别,计算量会非常大,通常也没有必要直接使用像素级别的图像特征,因为图像的像素值在空间上的冗余性是比较大的,所以可以考虑先用 PCA 算法对高维的特征向量进行降维,再用降维之后的特征向量来做人脸识别的工作。接下来就来看一下如何对这些数据进行降维。
首先进行数据的预处理,读取样本的每一图片矩阵,将每一图片矩阵转化为一个列向量,将所有图片对应的列向量组成一个装有所有样本图片的矩阵。得到矩阵 A 后,求取矩阵 A 中每一行的平均值,并将矩阵 A 每一行都减去对应行的平均值。这个平均值其实也对应一幅和人脸图像同样大小的图像,如下图所示。

图 21 平均值对应的人脸图像
得到数据预处理后的矩阵,就可以求取其协方差矩阵,再求其特征值和特征向量,即可根据特征值的大小取相应的特征向量组建投影子空间。下图是 ORL 数据库中最大的 16 个特征值的特征向量对应的主成分人脸图像。
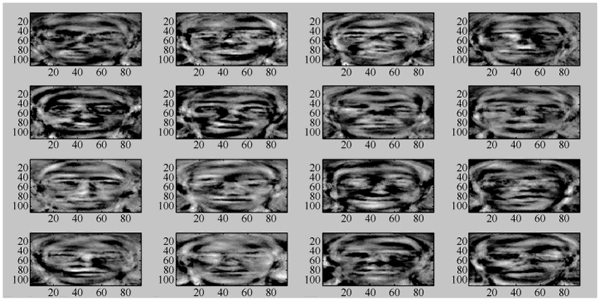
图 22 主成分人脸图像
可以看出,这些主成分人脸图像基本上保留了人脸最主要的轮廓和纹理特征。在样本空间足够大的情况下,绝大部分人脸可以由这些特征脸加权之后拼合而成。
建立完特征脸之后,人脸识别就变得简单很多,把装有样本空间中所有图片的矩阵 A 投射到特征脸空间中,每一张人脸图片都会得到对应特征脸加权数,可以将其理解为特征脸空间中的坐标值。以降到 68 维为例,降维之前的特征矩阵为 10304×400,降维之后的特征矩阵为 68×400,特征存储量少了整整 150 倍。这不仅极大地节省了资源,而且保留了人脸的主要信息。
什么是数据降维
介绍 PCA 算法之前,先说明一下数据维度的概念。假设有 5 只猫,每只猫的毛色、体型、身高、体重、年龄、性别等特征各不相同。这里的猫就是对象,“猫”这个称呼是这个对象的标签,毛色、体型、体重等特征就是对象的属性。
在实际的图像识别过程中,可能有大量的猫、狗的图片,所需的对象的属性也有多个,这些属性的个数就是维度。维度越高,数据量越大,占用的磁盘空间和内存就越多。
但很多时候用不到这么多的信息,或者因为其他的一些原因,不能在太高的维度下进行操作,这时就需要进行数据降维。
具体来说,数据降维主要指的是按照一定的方法降低数据的特征维度,这样做的原因主要有三个:
- 数据中往往存在很多字段,但是一些字段对于结果是没有意义的,或者意义极小,因此要根据实际情况对数据进行降维,使处理后的数据更加有益于得到精确的结果。
- 在某些场景下,数据维度特别高,而硬件计算或者存储资源比较有限,没有办法直接处理高维度的数据,只能通过一定的方法,将高维度的数据转换到较低维度的特征空间,从而实现对相关数据的处理。
- 在实际应用场景下所用到的特征数据维度大多在 3 维以上,进行数据分析时,有时需要对相关特征数据进行可视化分析,而高于 3 维的数据是没有办法实现可视化的,因此只能将高维数据降为 3 维或 2 维,再对降维之后的数据进行可视化分析。数据可视化效果图如下图所示。

图 1 数据可视化效果图
综上所述,数据降维的意义如下:克服维度灾难,获取本质特征,节省存储空间,去除无用的噪声,实现数据可视化。
PCA算法是什么
主成分分析(PCA)是一种常用的数据分析方法,其思想是将 n 维特征映射到 k 维空间中,其中 k<n,这 k 维特征是全新的正交特征,是重新构造出来的,而不是简单地从 n 维特征中去除其余 n-k 维特征。PCA 算法可以通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维数据的降维。这种算法和监督学习算法中的 Fisher 线性判别分析比较类似,都是将数据投影到一个可分性更好的投影空间,但 PCA 算法是一种非监督学习算法,不需要任何数据标签即可做到对数据进行变换投影。
PCA 算法通过找到一组线性变换的向量来对原始数据进行投影,那么如何衡量投影的优劣呢?
在数学上通常有两种方法衡量投影的优劣:
- 最大化投影数据的方差,即最大方差理论;
- 最小化平均投影代价,即最小平方误差理论。平均投影代价是指数据点和它们的投影之间的平均平方距离。
值得注意的是,这两种方法在数学上是完全等价的,下面就基于这两种方法来进行 PCA 算法的推导。
1) 最大方差理论
在信号处理中认为信号有较大的方差,噪声有较小的方差,信噪比就是信号与噪声的方差比,它越大越好。因此认为,最好的 k 维特征是将 n 维样本点变换为k维后,每一维上的样本方差都尽可能大。首先,考虑在一维空间(k=1)中的投影。可以使用 n 维向量 u 定义这个空间的方向。假定选择一个单位向量 u,使得 uTu=1。注意,这里只对 u 的方向感兴趣,而对 u 本身的大小不感兴趣。

图 2 投影图
图 2 中的点表示原样本点 xi,u 是直线的斜率,也是直线的方向向量,而且是单位向量,直线上的点表示原样本点 xi 在 u 上的投影。由数据投影的基本原理知道,投影点与原点的距离是 xiᵀu,由于这些原始样本点的每一维特征均值都为 0,因此投影到 u 上的样本点的均值仍然是 0。
假设原始数据集为 X,目标是找到最佳的投影空间 w=(w1,w2,…,wk),其中 wi 是单位向量且 wi 与 wj(i≠j)正交。何为最佳的 w?就是原始样本点投影到 w 上之后,使得投影后的样本点方差最大。由于投影后均值为 0,因此投影后的总方差为:
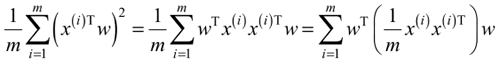
因为 x(i) 的均值为 0,所以等式右边小括号里的那部分其实就是原始数据集 X 的协方差矩阵(因为无偏估计的原因,一般协方差矩阵除以 m-1,这里用 m)。
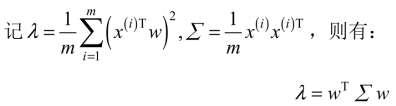
上式两边同时左乘 w,注意到 wwT=1(单位向量),则有:
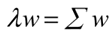
所以 w 其实是矩阵 ∑ 的特征值所对应的特征向量。欲使投影后的总方差最大,即λ最大,则最佳的投影向量 w 是特征值 λ 最大时对应的特征向量。因此,当将 w 设置为与具有最大的特征值 λ 的特征向量相等时,方差会达到最大值。这个特征向量被称为第一主成分。
可以用一种增量的方式定义额外的主成分,具体如下:在所有与那些已经考虑过的方向正交的所有可能的方向中,将新的方向选择为最大化投影方差的方向。如果考虑 k 维投影空间的一般情形,那么最大化投影数据方差的最优线性投影由数据协方差矩阵 ∑ 的 k 个特征向量 w₁,…,wk 定义,对应 k 个最大的特征值 λ₁,…,λk。
因此,只需要对协方差矩阵进行特征值分解,得到的前 k 大特征值对应的特征向量就是最佳的 k 维新特征,而且这 k 维新特征是正交的。得到前 k 个 u 以后,原始数据集 X 通过变换可以得到新的样本。
2) 最小平方误差理论

图 6 最小平方误差图
假设二维样本点如图 6 所示,按照前面讲解的最大方差理论,目标是求一条直线,使得样本点投影到直线上的点的方差最大。
从求解直线的思路出发,容易想到数学中的线性回归问题,其目标也是求解一个线性函数,使得对应直线能够更好地拟合样本点集合。如果从这个角度出发推导 PCA 算法,那么问题会转化为一个回归问题。回归时的最小二乘法度量的是样本点到直线的坐标轴距离。
比如这个问题中,特征是 x,类标签是 y。回归时最小二乘法度量的是距离 d。如果使用回归法来度量最佳直线,那么就是直接在原始样本上做回归。因此,可以选用另一种评价直线好坏的方法,即使用点到直线的距离 d′ 来度量。
现有 m 个样本点,每个样本点为 n 维。目标是最小化样本点与投影点之间的距离,称之为最小平方误差。
假设 xk 表示 p 维空间的 k 个点,zk 表示 xk 在超平面 D 上的投影向量,w=(w1,w2,…,wd)为 d 维空间的标准正交基,则最小平方误差理论可以转换为如下优化问题:
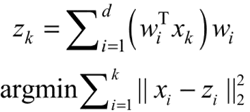
s.t.wiTwj=p(当 i=j 时 p=1,否则 p=0)
其中,wiTxk 为 xk 在 wi 基向量上的投影长度,wiTxkwi 为 wi 基向量的坐标值。
求解过程如下:
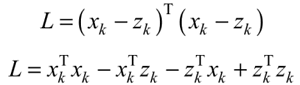
由于向量有内积性质 xTkzk=zTkxk ,可得:
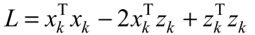
将 zk 的表达式代入得:
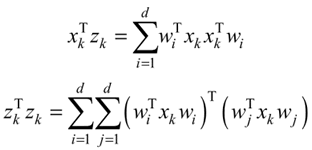
根据约束条件得:
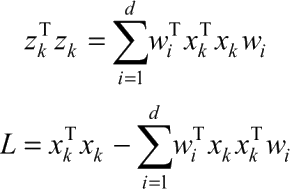
根据奇异值分解:
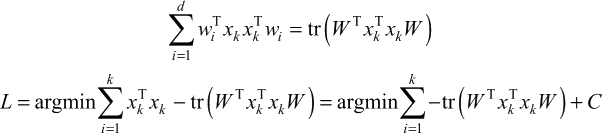
等价于带约束的优化问题:
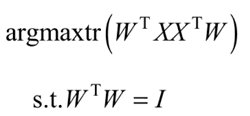
该问题的求解结果最佳超平面 W 与最大方差理论求解的最佳投影方向一致,即协方差矩阵的最大特征值所对应的特征向量,差别仅是协方差矩阵的一个倍数。
PCA算法求解步骤
经过前面对 PCA 算法的原理分析,假设有 n 个 m 维特征数据,可以得出 PCA 算法的处理流程如下:- 将原始数据按列组成 n 行 m 列矩阵 X。
- 计算 X 每一列的均值,将每一列数据减去均值,得到去中心化的结果。
- 求出矩阵X的协方差矩阵 Y。
- 求出协方差矩阵 Y 的特征值及对应的特征向量。
- 将得到的特征向量依据对应的特征值的大小按行排列成一个矩阵,取前 k 行组成矩阵 P。
- 令 Z=XP,矩阵 Z 即降到 k 维后的数据。
假设现在有 5 个 2 维数据 [-1,1]、[-2,-1]、[-3,-2]、[1,1]、[2,1] 组成的矩阵 X:
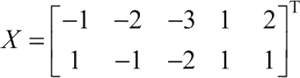
使用上述算法流程将这 5 个 2 维数据降维处理成 5 个 1 维数据,过程如下:
① 计算原始数据中每一列的均值为 [-0.6,0],将每一列数据减去均值,得到去中心化的结果 X₂ 如下:
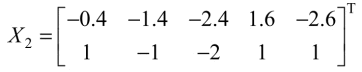
②求出矩阵 X₂ 的协方差矩阵为 Y=
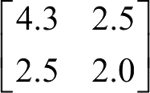
③ 求出协方差矩阵 Y 的特征值为 5.902 和 0.398,对应的特征向量组成的矩阵为:
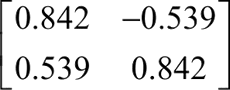
④ 将得到的特征向量依据特征值的大小按行排列成一个矩阵,组成矩阵 P=
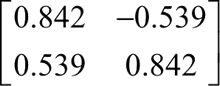
这里由于第一个特征值本来就大于第二个特征值,所以排序后得到的矩阵和步骤 ③ 中特征向量组成的初始矩阵一致。
⑤ 用矩阵 P 的第一列 P₁ 表示转换矩阵,令 Z=XP₁,得到的 1 维向量即降到 1 维的特征数据 Z=[0.2-1.7-3.0 1.9 2.7]ᵀ。
对该组数据进行降维处理的结果如下图所示:

图 19 PCA算法结果示意图
这里需要注意一下特征数据的去中心化的问题。
所谓去中心化,就是将样本X中的每个观测值都减去样本均值,这样做的好处主要是能够使求解协方差矩阵变得更容易。
另外,为了简单起见,上述示例的特征数据维度并不高,可以直接进行矩阵分解计算。但是在真实的应用案例当中,特征数据的维度通常都很高,PCA 通常是数值近似分解,而非求特征值、奇异值得到解析解,所以当使用梯度下降法等算法进行PCA的时候,最好先对数据进行标准化,这有利于梯度下降法的收敛。
PCA算法实例
在较早的时候,人脸识别领域还没有使用深度学习来提取特征,当时有研究人员使用 PCA 算法来提取人脸特征。这里以人脸识别经典数据库 ORL 为例,如下图所示,看一下如何使用 PCA 算法来做人脸识别。
图 20 ORL数据库示例图像
ORL 数据库中的每张图片大小是 92×112 像素,转换成特征向量共有 10304 维。如果直接使用这个维度来进行识别,计算量会非常大,通常也没有必要直接使用像素级别的图像特征,因为图像的像素值在空间上的冗余性是比较大的,所以可以考虑先用 PCA 算法对高维的特征向量进行降维,再用降维之后的特征向量来做人脸识别的工作。接下来就来看一下如何对这些数据进行降维。
首先进行数据的预处理,读取样本的每一图片矩阵,将每一图片矩阵转化为一个列向量,将所有图片对应的列向量组成一个装有所有样本图片的矩阵。得到矩阵 A 后,求取矩阵 A 中每一行的平均值,并将矩阵 A 每一行都减去对应行的平均值。这个平均值其实也对应一幅和人脸图像同样大小的图像,如下图所示。

图 21 平均值对应的人脸图像
得到数据预处理后的矩阵,就可以求取其协方差矩阵,再求其特征值和特征向量,即可根据特征值的大小取相应的特征向量组建投影子空间。下图是 ORL 数据库中最大的 16 个特征值的特征向量对应的主成分人脸图像。

图 22 主成分人脸图像
可以看出,这些主成分人脸图像基本上保留了人脸最主要的轮廓和纹理特征。在样本空间足够大的情况下,绝大部分人脸可以由这些特征脸加权之后拼合而成。
建立完特征脸之后,人脸识别就变得简单很多,把装有样本空间中所有图片的矩阵 A 投射到特征脸空间中,每一张人脸图片都会得到对应特征脸加权数,可以将其理解为特征脸空间中的坐标值。以降到 68 维为例,降维之前的特征矩阵为 10304×400,降维之后的特征矩阵为 68×400,特征存储量少了整整 150 倍。这不仅极大地节省了资源,而且保留了人脸的主要信息。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: