最大子序列和问题(分治法Java实现)
所谓最大子序列和问题,本节讨论的是求数组中最大连续子序列的和。
例如给定数组 A={6,3,-11, 5, 8, 15, -2, 9, 10, -5},则最大连续子序列的和为 45,即 5+8+15+(-2)+ 9+10 = 45。
当 n>1 时,可利用分治法求解该问题,令 mid=(left+right)/2,最大子序列的和可能出现在以下 3 个区间内:
1) 该子序列完全落在左半区间,即 a[0…mid-1]中,可采用递归将问题缩小在左半区间,通过调用自身 maxLeftSum = MaxSubSum(a,left,mid)求出最大连续子序列的和 maxLeftSum。
2) 该子序列完全落在右半区间,即 [mid…n-1]中,类似地,可通过调用自身 maxRightSum =MaxSubSum(a,mid,right) 求出最大连续子序列的和 maxRightSum。
3) 该子序列落在两个区间之间,横跨左右两个区间,需要从左半区间求出:
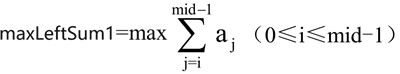
从右半区间求出:
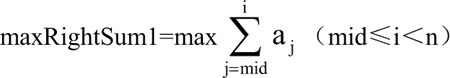
最大连续子序列的和为
最后需要求出这 3 种情况连续子序列的和的最大值,即 maxLeftSum1+maxRightSum1,maxLeftSum, maxRightSum 的最大值就是最大连续子序列的和。
递归调用自身求左半区间的最大连续子序列的和 maxLeftSum:
递归调用自身求右半区间最大连续子序列的和 maxRightSum:
求左半区间中从 mid-1 到 i 的最大子序列的和 maxLeftSum1:
求右半区间从 mid 到 i 的最大子序列的和 maxRightSum1:
求以上 3 种情况的最大值,即最大连续子序列的和:
例如给定数组 A={6,3,-11, 5, 8, 15, -2, 9, 10, -5},则最大连续子序列的和为 45,即 5+8+15+(-2)+ 9+10 = 45。
最大子序列和问题解析
假设要求子序列的和至少包含一个元素,对于含 n 个整数的数组 a[],若 n=1,则表示该数组中只有一个元素,返回该元素。当 n>1 时,可利用分治法求解该问题,令 mid=(left+right)/2,最大子序列的和可能出现在以下 3 个区间内:
1) 该子序列完全落在左半区间,即 a[0…mid-1]中,可采用递归将问题缩小在左半区间,通过调用自身 maxLeftSum = MaxSubSum(a,left,mid)求出最大连续子序列的和 maxLeftSum。
2) 该子序列完全落在右半区间,即 [mid…n-1]中,类似地,可通过调用自身 maxRightSum =MaxSubSum(a,mid,right) 求出最大连续子序列的和 maxRightSum。
3) 该子序列落在两个区间之间,横跨左右两个区间,需要从左半区间求出:
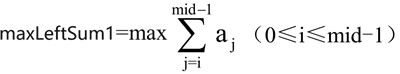
从右半区间求出:
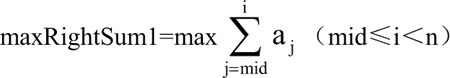
最大连续子序列的和为
maxLeftSum1+ maxRightSum1。最后需要求出这 3 种情况连续子序列的和的最大值,即 maxLeftSum1+maxRightSum1,maxLeftSum, maxRightSum 的最大值就是最大连续子序列的和。
分治法解决最大子序列和问题
算法实现如下:
public class MaxSubSum {
int GetMaxNum(int x, int y, int z) {
if (x > y && x > z)
return x;
if (y > x && y > z)
return y;
return z;
}
int GetMaxSubSum(int a[], int left, int right) {
int mid, maxLeftSum, maxRightSum, i, tempLeftSum, tempRightSum;
int maxLeftSum1, maxRightSum1;
if (right - left == 1) { // 如果当前序列只有一个元素
return a[left];
}
mid = (left + right) / 2; // 计算当前序列的中间位置
maxLeftSum = GetMaxSubSum(a, left, mid);
maxRightSum = GetMaxSubSum(a, mid, right);
// 计算左边界最大子序列的和
tempLeftSum = 0;
maxLeftSum1 = a[mid - 1];
for (i = mid - 1; i >= left; i--) {
tempLeftSum += a[i];
if (maxLeftSum1 < tempLeftSum)
maxLeftSum1 = tempLeftSum;
}
// 计算右边界最大子序列的和
tempRightSum = 0;
maxRightSum1 = a[mid];
for (i = mid; i < right; i++) {
tempRightSum += a[i];
if (maxRightSum1 < tempRightSum)
maxRightSum1 = tempRightSum;
}
// 返回当前序列最大子序列的和
return GetMaxNum(maxLeftSum1 + maxRightSum1, maxLeftSum, maxRightSum);
}
public static void main(String args[]) {
MaxSubSum S = new MaxSubSum();
int a[] = {6, 3, -11, 5, 8, 15, -2, 9, 10, -5}, s;
System.out.println("元素序列: ");
for (int i = 0; i < a.length; i++)
System.out.printf("%5d", a[i]);
System.out.println();
s = S.GetMaxSubSum(a, 0, a.length);
System.out.printf("最大连续子序列的和:%d\n", s);
}
}
程序运行结果如下:
元素序列:
6 3 -11 5 8 15 -2 9 10 -5
最大连续子序列的和:45
下面简要分析以上代码。若子序列中只有一个元素,则返回该元素,即:
if (right - left == 1) { // 若当前子序列只有一个元素
return a[left];
}
递归调用自身求左半区间的最大连续子序列的和 maxLeftSum:
maxLeftSum = GetMaxSubSum(a,left,mid);
递归调用自身求右半区间最大连续子序列的和 maxRightSum:
maxRightSum = GetMaxSubSum(a,mid,right);
求左半区间中从 mid-1 到 i 的最大子序列的和 maxLeftSum1:
tempLeftSum = 0;
maxLeftSum1 = a[mid-1];
for (i = mid - 1; i >= left; i--) {
tempLeftSum += a[i];
if (maxLeftSum1 < tempLeftSum)
maxLeftSum1 = tempLeftSum;
}
求右半区间从 mid 到 i 的最大子序列的和 maxRightSum1:
tempRightSum = 0;
maxRightSum1 = a[mid];
for (i = mid; i < right; i++) {
tempRightSum += a[i];
if (maxRightSum1 < tempRightSum)
maxRightSum1 = tempRightSum;
}
求以上 3 种情况的最大值,即最大连续子序列的和:
return GetMaxNum(maxLeftSum1 + maxRightSum1, maxLeftSum, maxRightSum);
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: