最长上升子序列（C++实现）

给定序列（a1，a2，…，an），从前向后取其中的若干元素组成一个子序列，若该子序列是升序排序的，则称之为上升子序列。

例如，序列（1，7，3，5，9，4，8）有上升子序列如（1，7）、（3，4，8）和其他子序列，所有最长的上升子序列的长度都是 4，例如（1，3，5，8）。

求解给定序列的最长上升子序列的长度：

• 输入： 第 1 行为序列的长度 n（1≤n≤1000）；第 2 行为序列的 n 个元素，每个元素都为 0~10000 的整数。
• 输出：输出给定序列的最长上升子序列的长度。

算法设计

本题为求解最长上升子序列的长度的问题：

• 状态表示：dp[i] 表示以 a[i] 结尾的最长上升子序列的长度。
• 状态转移：对于 1≤j<i，若 a[j]<a[i]，则可以将 a[i] 放在以 a[j]结尾的最长上升子序列后面，得到的长度为 dp[j]+1。
• 状态转移方程：dp[i]=max(dp[i], dp[j]+1)。
• 边界条件是 dp[0]=0。
• 求解目标：max(dp[i])。

算法实现

int dp[maxn]; //dp[i]表示以a[i]结尾的最长上升子序列的长度
int main() {
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    int ans=0;
    memset(dp,0,sizeof(dp));
    for(int i=1;i<=n;i++) {
        dp[i]=1;
        for(int j=1;j<i;j++)
            if(a[j]<a[i]) //a[j]<a[i]，将a[i]放在以a[j]结尾的最长上升子序列后面，长度加1
                dp[i]=max(dp[i],dp[j]+1);
        if(dp[i]>ans)
            ans=dp[i]; //更新最大值
    }
    printf("%d\n",ans);
    return 0;
}

以上算法的时间复杂度为 O(n^2)，空间复杂度为 O(n)。

算法优化

根据上升子序列的特性，可设置一个辅助数组 d[] 来求解最长上升子序列，len 表示最长上升子序列的长度。

算法步骤如下：

• 1) 初始化：d[1]=a[1]，len=1。
• 2) 枚举 i=2..n，将 a[i] 与 d[len]（d[] 的最后一个元素）做比较。
• 3) 若 a[i]=d[len]，则什么也不做，继续下一次循环。
• 4) 若 a[i]>d[len]，则将 a[i] 添加到 d[] 尾部，即 d[++len]=a[i]。
• 5) 若 a[i]<d[len]，则用 a[i] 替换 d[] 中第 1 个大于或等于 a[i]的数。

在 d[] 中查找第 1 个大于或等于 a[i] 的数时，既可以采用二分查找（d[] 自身有序），也可以直接调用函数 lower_bound()，该函数也是采用二分查找实现的，每次查找的时间复杂度都为 O(logn)。

为什么可以这么做呢？本题求解最长上升子序列，所以对前两种情况都很容易理解。若 a[i]<d[len]，则将 a[i] 替换 d[] 中第 1 个大于或等于 a[i] 的数，这是因为在不影响 d[] 长度的情况下，d[] 中的元素越小，就越可能得到更长的上升子序列。

完美图解

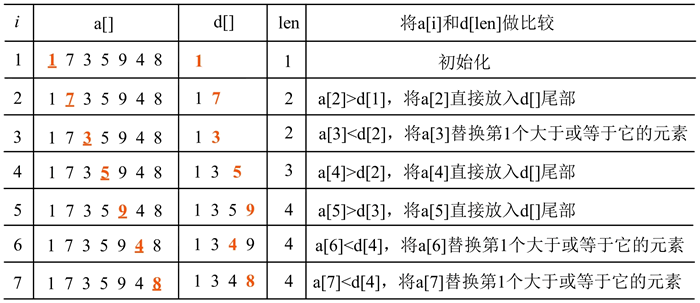
输入样例“1735948”，求解其最长上升子序列，过程如下图所示：

int d[maxn]; //d[1]为辅助数组
int main() {
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    int len=1;
    d[1]=a[1];
    for(int i=2;i<=n;i++) {
        if(a[i]==d[len]) continue;
        if(a[i]>d[len])
            d[++len]=a[i];
        else //a[i]覆盖d[]中第1个大于或等于a[i]的数
            *lower_bound(d+1,d+len+1,a[i])=a[i];
    }
    printf("%d\n",len);
}

求解最长上升子序列的优化算法的时间复杂度为 O(nlogn)，空间复杂度为 O(n)。