分治算法详解(Java实现,图文并茂)
分治法是将一个规模为 N 的问题分解为 K 个规模较小的子问题进行求解,这些子问题相互独立且与原问题性质相同。求出子问题的解,就可以得到原问题的解。
快速排序、归并排序、最大子序列和、求 x 的 n 次幂等问题都可以利用分治策略的算法思想实现。
经典的归并排序、快速排序、二分查找就是利用分治算法的思想,以一个经典的问题来说明分治法的好处。有 100 枚硬币,其中一枚是假币,真币和假币的重量是不一样的,假币会略轻一些。如何快速找出这枚假币呢?
为了找出这枚假币,可以用天平一枚一枚硬币来称重,如果两枚硬币的重量不同,就找出了假币。采用这种方法需要 50 次称重才能找出假币。有没有更好的称重办法呢?
可以把 100 枚硬币平均分成 3 份,每份硬币的数量分别是 33、33 和 34。用天平分别对这 3 份硬币称重,若前两份硬币的重量相等,则说明假币在最后一份硬币中;否则,假币在前两份硬币中较轻的一份中。下面分情况讨论:
1) 若假币在前两份硬币中,则需要在较轻的硬币中寻找假币。将 33 枚硬币分为 3 份,每份硬币数量均为 11 枚,继续用天平对每份硬币称重,重量较轻的必定包含假币。
2) 若假币在 34 枚硬币中,则将 34 枚硬币分为 3 份,每份硬币的数量分别是 11、11 和 12,,若前两份硬币的重量相等,则假币在第 3 份硬币中;否则,假币在前两份中较轻的硬币中。
3) 若假币在第 3 份硬币中,则继续将硬币分成 3 份,每份硬币的数量分别是 4、4 和 4,假币在其中较轻的硬币中。
4) 若假币在 11 枚硬币中,则将其分成 3 份,每份硬币的数量分别是 4、4 和 3,若前两份硬币的重量相同,则假币在第 3 份硬币中;否则,假币在前两份较轻的硬币中。
5) 若假币在 3 枚硬币中,则继续将其分成 3 份,每份硬币的数量为 1、1 和 1,若前两份硬币的重量相同,则假币在最后一份硬币中;否则,假币在前两份中较轻的一份中。
6) 若假币在 4 枚硬币中,则将其分成 3 份,每份硬币的数量为 1、1 和 2,若前两份硬币的重量相同,则假币在最后一份硬币中;否则,假币在前两份较轻的硬币中。
7) 若假币在 2 枚硬币中,则将其划分为 2 份,每一份只有一枚硬币,重量较轻者为假币。
根据以上分析,找出假币只需要 5 次称重即可,显然这种方法找出假币的效率非常高。
分治算法的执行分为以下过程:
算法伪代码如下:
归并排序就是利用分治算法的思想实现排序的典型例子,它采用分治策略将问题分成一些小的问题,然后递归求解,而治的阶段则将分解阶段得到的结果合并在一起,从而完成分而治之,得到最终的排序结果。
对序列 {12,9,23,5,16,31,20,28} 进行归并排序的过程如下图所示:
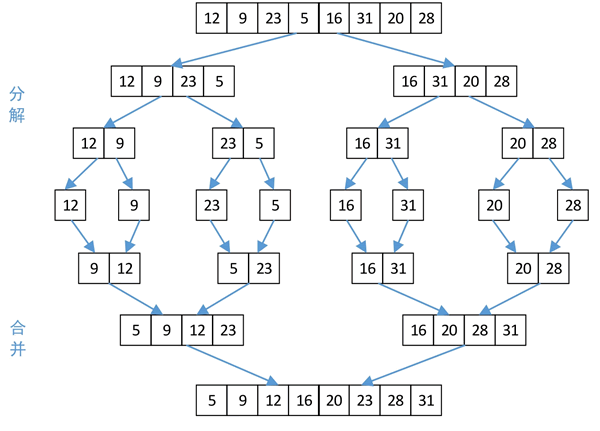
图 1 归并排序的分治算法求解过程
利用分治策略的归并排序算法实现如下:
快速排序、归并排序、最大子序列和、求 x 的 n 次幂等问题都可以利用分治策略的算法思想实现。
分治算法的基本思想
分治,即“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单地直接求解,原问题的解即子问题的解的合并。经典的归并排序、快速排序、二分查找就是利用分治算法的思想,以一个经典的问题来说明分治法的好处。有 100 枚硬币,其中一枚是假币,真币和假币的重量是不一样的,假币会略轻一些。如何快速找出这枚假币呢?
为了找出这枚假币,可以用天平一枚一枚硬币来称重,如果两枚硬币的重量不同,就找出了假币。采用这种方法需要 50 次称重才能找出假币。有没有更好的称重办法呢?
可以把 100 枚硬币平均分成 3 份,每份硬币的数量分别是 33、33 和 34。用天平分别对这 3 份硬币称重,若前两份硬币的重量相等,则说明假币在最后一份硬币中;否则,假币在前两份硬币中较轻的一份中。下面分情况讨论:
1) 若假币在前两份硬币中,则需要在较轻的硬币中寻找假币。将 33 枚硬币分为 3 份,每份硬币数量均为 11 枚,继续用天平对每份硬币称重,重量较轻的必定包含假币。
2) 若假币在 34 枚硬币中,则将 34 枚硬币分为 3 份,每份硬币的数量分别是 11、11 和 12,,若前两份硬币的重量相等,则假币在第 3 份硬币中;否则,假币在前两份中较轻的硬币中。
3) 若假币在第 3 份硬币中,则继续将硬币分成 3 份,每份硬币的数量分别是 4、4 和 4,假币在其中较轻的硬币中。
4) 若假币在 11 枚硬币中,则将其分成 3 份,每份硬币的数量分别是 4、4 和 3,若前两份硬币的重量相同,则假币在第 3 份硬币中;否则,假币在前两份较轻的硬币中。
5) 若假币在 3 枚硬币中,则继续将其分成 3 份,每份硬币的数量为 1、1 和 1,若前两份硬币的重量相同,则假币在最后一份硬币中;否则,假币在前两份中较轻的一份中。
6) 若假币在 4 枚硬币中,则将其分成 3 份,每份硬币的数量为 1、1 和 2,若前两份硬币的重量相同,则假币在最后一份硬币中;否则,假币在前两份较轻的硬币中。
7) 若假币在 2 枚硬币中,则将其划分为 2 份,每一份只有一枚硬币,重量较轻者为假币。
根据以上分析,找出假币只需要 5 次称重即可,显然这种方法找出假币的效率非常高。
分治法的实现过程
分治法就是将原问题分解为若干子问题进行求解,这些子问题形式相同,且相互独立。这与递归很相似,因此,分治算法常使用递归的方式实现。分治算法的执行分为以下过程:
- 分(Divide):将原问题分解为规模更小的子问题;
- 治(Conquer):递归求解子问题,若问题足够小,则直接求解;
- 合并(Combine):将子问题的解合并为原问题的解。
算法伪代码如下:
Divide_and_Conquer(P) // 输入问题 P
{
if P's scale ≤ n0 // 若问题的规模小于 n0
return (P's fundamental solution);
divide P into smaller sub problems P1, p2, ..., Pk; // 将问题的规模缩小为更小的子问题
for i←1 to k
yi ← Divide_and_Conquer(Pi) // 利用递归求解子问题
return Merge(y1, y2, ..., yk) // 合并子问题
}
分治法解决的问题特征
利用分治法能解决的问题一般具有以下几个特征:- 原问题与分解后的子问题具有相同的模式,即问题具有最优子结构的性质;
- 原问题分解成的子问题可以独立求解,即子问题之间没有相关性,这是分治法和动态规划最明显的区别;
- 子问题的结果可合并成原问题的结果,且合并不能太复杂;
- 具有分解终止条件。当问题规模变得足够小时,可以直接求解。
归并排序就是利用分治算法的思想实现排序的典型例子,它采用分治策略将问题分成一些小的问题,然后递归求解,而治的阶段则将分解阶段得到的结果合并在一起,从而完成分而治之,得到最终的排序结果。
对序列 {12,9,23,5,16,31,20,28} 进行归并排序的过程如下图所示:

图 1 归并排序的分治算法求解过程
利用分治策略的归并排序算法实现如下:
public class MergeSort {
int temp[]; // 临时数组
MergeSort(int n) {
temp = new int[n];
}
void merge(int a[], int low, int mid, int high) // 合并两个子区间中的元素
{
int i = low, j = mid + 1, k = low; // i 和 j 分别指向需要合并的两个子序列的第一个元素
while (i <= mid && j <= high) // 还没有扫描完毕
{
// 将较小数存储在 temp 中,并且后移指针
if (a[i] < a[j])
temp[k++] = a[i++];
else
temp[k++] = a[j++];
}
while (i <= mid) // 左半区间还有元素
temp[k++] = a[i++];
while (j <= high) // 右半区间还有元素
temp[k++] = a[j++];
for (i = low; i <= high; i++) // 把元素重新复制到数组 a[] 中
a[i] = temp[i];
}
void merge_sort(int a[], int l, int r) // 归并排序算法
{
if (l >= r) // 递归出口:每个区间只有一个元素
return;
int mid = (l + r) / 2;
merge_sort(a, l, mid); // 归并排序左半区间
merge_sort(a, mid + 1, r); // 归并排序右半区间
merge(a, l, mid, r); // 将左右区间中的元素合并
}
public static void main(String args[]) {
int n;
int a[] = {12, 9, 23, 5, 16, 31, 20, 28};
n = a.length;
MergeSort MS = new MergeSort(n);
MS.merge_sort(a, 0, n - 1); // 对第 1~n 个元素进行归并排序
for (int i = 0; i < n; i++)
System.out.printf("%4d", a[i]);
}
}
程序运行结果如下:
5 9 12 16 20 23 28 31
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: