分词算法有哪些?(新手必看)
现在分词工具的主流方法基本都是最短路径分词,下面逐一介绍。
至于词表可以使用通用汉语词表,也可以使用自己整理收集的词表,例如一些专业领域的词表(电子商务和医药等)。
给定一个句子,具体如何基于词表查找分词呢?如果仅是对词表进行随意查找,那么很容易把一些长词切分为短词。例如,“中华人民共和国成立了”被切分为“中华”、“人民”、“共和国”、“成立了”。“中华人民共和国”此类词一般有独立的意义,被区分为短词之后,其意义减弱甚至消失了。因此随意查找肯定不是好方案。
最大匹配法的提出就是为了避免此类问题。
正向最大匹配是指在查找词表时,优先匹配最长的那个词,如果匹配上更长的词,则抛弃短词。例如前面的“中华人民共和国”,如果词表里有这个词,则直接匹配成功,如果没有这个长词,就往下切分。
所谓正向,就是从左向右逐字搜索。还以“中华人民共和国”为例,搜索过程是先搜索“中华”,如果词表里有这个词则记录下来,即使没有也继续搜索,下一个搜索的词是“中华人”,有没有该词都会继续搜索,如果有,则记录,下一个是“中华人民”,以此类推,直到找到“中华人民共和国”这个词后停止。如果词表里没有这个词,则往回退,找那个次长的。
这里如果用词表的词在句子中搜索可以吗?当然可以,但是,如果词表有 50 万个词(这个量级是通用词表的常见数量),那么每次搜索就要遍历 50 万次,效率太低。
为了提高搜索的性能,往往使用一种称为 Trie 树的数据结构,也叫字典树。
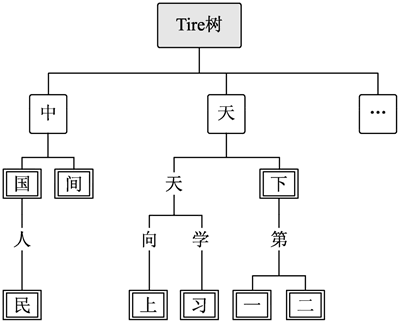
图 1 Trie树
Trie 树的设计思路是以树形组织词表,根节点只有一个,其没有实际意义,只是用来保存所有一级节点的指针。从第一级节点开始,每级的每个节点都保存一个字。例如“天天向上”这个词,在 Trie 树里,第一级就是“天”,第二级是“天”,第三级是“向”,第四级是“上”。完全靠文字描述可能不是很清楚,可以参考图 1。
词表里所有的词的第一个字都在 Trie 树的第一级,第二个字都在第二级,以此类推。所有与第一个字相同的词,都被合并到一个子树下面。例如,“中国”与“中间”的第一字都是“中”,则共享一个父节点。
在图 1 中,双边框的字都表示词的结束,如“中国”的“国”字,在查找的时候可以通过这个结束标示来判断是否可以结束查找。
如何使用树结构呢?我们再模拟一遍搜索的过程。例如,“中国人民无条件支持你”,从“中”开始即 Trie 树的根节点开始查找,发现里面有“中”这个字,而且“中”这个字并没有结束标示,意思就是“中”不能成为一个词。
根节点保存着所有词的第一个字,那么如何能快速查找呢?遍历吗?其显示性能太低了。解决办法其实很简单,在构造字典树的时候把下面的节点做一个排序即可。
在数据结构的排序中,对于有效列表,可以进行最快的二分查找。当然也有一些 Trie 树的变种,把这种多叉树的结构改为二叉树,其实就是为了进行天然的二分查找。还有更快的方法,就是对每一层都使用一个Hash表来存储,这样在 O(1) 的时间内就可以完成查找,但代价是占用的内存空间很大。
我们继续上面的查找,找到“中”之后开始找“中国”,“中”下面有“国”字,同时“国”字有结束标示,也就是说“中国”后面的下一个字如果不是“人”字,在 Trie 树里没找到下一个字,那么就可以结束查找而返回“中国”。但现在“中国”的后面正好是“人”字,那么能找到就继续找,因为“人”字没有结束标示,下一个字是“民”,这样就到达了树的最低层,这里的所有节点都是有结束标示的。这样就把“中国人民”分词成功,虽然它中间包含“中国”这个词,但是这个词比“中国人民”短,因此以长的词为准。
所谓反向最大匹配,就是把本来从左往右匹配改为从右往左匹配。也就是“中国人民”的匹配方向从“中”、“国”、“人”、“民”,改为“民”、“人”、“国”、“中”,同时为了保持字典树的结构匹配,树的顺序也改为把词的最后一个字作为第一级,把第一个字作为最后一级的叶子节点,其他使用方式全部相同。
为什么反向最大匹配比正向最大匹配更好用?这其实没有什么底层理论支撑,只是通过实验得出的结论。实验统计得出,正向最大匹配的错误率大概在 1/150,而反向最大匹配的错误率大概在 1/250,也就是说反向最大匹配并没有完全消除切分错误,只是降低了错误率。
所谓最短路径分词,简单地说就是把所有分词的可能性都列出来,然后寻找概率最大的那个路径。因为概率本来是相乘的,计算不方便,一般会使用 log 函数把乘法改为加法,而小于 1 的数值取对数之后会变为负数,并且所有的概率都为负,而且使用的是加法,所以不需要一直带着负号,再在取 log 的基础上取负。这样 -log 取值最小,也就是原值最大,因此叫最短路径,而不是最长路径,如下图所示。
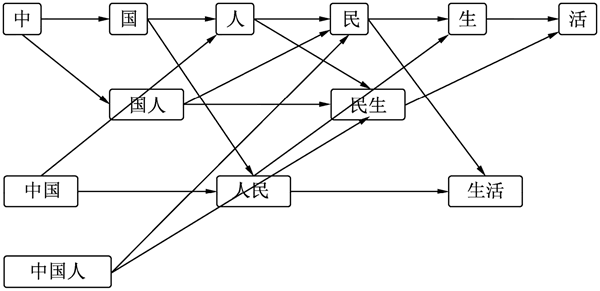
图 2 最短路径的词网
此处大概演示一下算法的流程。以“中国人民生活”为例,先使用词表匹配分词,把所有可能的词都分出来,这里就不是最大匹配,而是全匹配,如图 2 所示。
“中国人民生活”可以分为“中”、“国”、“人”、“民”、“生”、“活”、“中国”、“国人”、“人民”、“民生”、“生活”、“中国人”等,然后可以以组成原来的句子为原则连接为一个词网。例如,“中”后面可以接“国人”,但不能接“中国”,因为这样组成的句子就成“中中国”了,同样不可以接“人民”,这样就少字了。最终连接好的词网如图 2 所示。
有了词网就可以寻找一个最优路径。那么以什么原则确定是否最优呢?也就是在词网节点之间的边上的权重使用什么值呢?一般使用的是二元词法(2-gram),这是一个统计概率。
例如“中国”后面跟“人”的概率,可以通过 count("中国人") 或 count("中国") 语句来计算。count(x) 语句的意思是语料库中词 x 的出现次数。当然有些非常少见的组合在语料库中可能没有涵盖,但不能认为其概率就是 0,还需要做平滑等操作。
有了图结构,也有了路径权重,那么求最短路径就有很多方法了,如数据结构关于图的 Dijkstra(迪杰斯特拉)算法。常用的是 Viterbi(维特比)算法,这个算法用来给 HMM(隐马尔可夫模型)算法的解码问题求解,在分词工具里分完词后还要进行基础版的命名实体识别 NER,否则遇到人名和公司名之类的词全部会被分为单字。很多工具都需要实现 HMM 算法,这样两处场景用一个算法不是更省力吗?
HMM 就是比马尔可夫模型多了一个隐藏变量的版本。正常的马尔可夫模型的逻辑是当前状态的概率基于前一个状态。例如,今天的天气依赖于昨天的天气,昨天是晴天,今天还是晴天的概率是 60%。常见的 n-gram 其实也是这个逻辑。
HMM 假设决定当前状态的是当前的隐藏状态,而当前的隐藏状态则依赖于前一个隐藏状态。例如,我们不关注天气而关注温度,那么假设温度完全是由天气决定的,那么今天的温度是多少度由今天的天气决定,而今天的天气则由前一天的天气决定,这样就形成了一个 HMM。
所谓的 Viterbi 算法,就是一个动态规划求最优解的方法。如果读者尚未学习过 HMM,看不懂这里的解释也没关系,可以把这个概念当作一个黑盒,只需要知道应该输入什么并了解输出结果表达的意思就可以了。
很多知识往往不是独立的,而是与其他知识相关联的,这时多数人喜欢把所有的知识点都弄明白,再来学习这个知识点,这也是人的天性,不过这样的学习效率不高,因为知识点的依赖有时候不像教科书那样是从前往后循序渐进排列的,这样容易导致一个知识点不懂就难以继续学习下去。如果有了黑盒思维,可以先把这个知识点封装起来,只关心其输入与输出,而不关心内部的实现,把外部的整体知识体系学明白,然后研究黑盒的内部,这样往往会起到事半功倍的效果。
正向最大匹配
分词最简单的方法是先整理出一个词表,然后在需要被分词的句子中逐个查找,如果匹配,则认为这是一个词。例如“我们一起去吃饭”,通过词表能分出“我们”、“一起”、“吃饭”等词。至于词表可以使用通用汉语词表,也可以使用自己整理收集的词表,例如一些专业领域的词表(电子商务和医药等)。
给定一个句子,具体如何基于词表查找分词呢?如果仅是对词表进行随意查找,那么很容易把一些长词切分为短词。例如,“中华人民共和国成立了”被切分为“中华”、“人民”、“共和国”、“成立了”。“中华人民共和国”此类词一般有独立的意义,被区分为短词之后,其意义减弱甚至消失了。因此随意查找肯定不是好方案。
最大匹配法的提出就是为了避免此类问题。
正向最大匹配是指在查找词表时,优先匹配最长的那个词,如果匹配上更长的词,则抛弃短词。例如前面的“中华人民共和国”,如果词表里有这个词,则直接匹配成功,如果没有这个长词,就往下切分。
所谓正向,就是从左向右逐字搜索。还以“中华人民共和国”为例,搜索过程是先搜索“中华”,如果词表里有这个词则记录下来,即使没有也继续搜索,下一个搜索的词是“中华人”,有没有该词都会继续搜索,如果有,则记录,下一个是“中华人民”,以此类推,直到找到“中华人民共和国”这个词后停止。如果词表里没有这个词,则往回退,找那个次长的。
这里如果用词表的词在句子中搜索可以吗?当然可以,但是,如果词表有 50 万个词(这个量级是通用词表的常见数量),那么每次搜索就要遍历 50 万次,效率太低。
为了提高搜索的性能,往往使用一种称为 Trie 树的数据结构,也叫字典树。
Trie树
Trie 树也叫字典树,它是一种数据结构,以相对有限的空间代价来提升分词查找的速度,如下图所示。
图 1 Trie树
Trie 树的设计思路是以树形组织词表,根节点只有一个,其没有实际意义,只是用来保存所有一级节点的指针。从第一级节点开始,每级的每个节点都保存一个字。例如“天天向上”这个词,在 Trie 树里,第一级就是“天”,第二级是“天”,第三级是“向”,第四级是“上”。完全靠文字描述可能不是很清楚,可以参考图 1。
词表里所有的词的第一个字都在 Trie 树的第一级,第二个字都在第二级,以此类推。所有与第一个字相同的词,都被合并到一个子树下面。例如,“中国”与“中间”的第一字都是“中”,则共享一个父节点。
在图 1 中,双边框的字都表示词的结束,如“中国”的“国”字,在查找的时候可以通过这个结束标示来判断是否可以结束查找。
如何使用树结构呢?我们再模拟一遍搜索的过程。例如,“中国人民无条件支持你”,从“中”开始即 Trie 树的根节点开始查找,发现里面有“中”这个字,而且“中”这个字并没有结束标示,意思就是“中”不能成为一个词。
根节点保存着所有词的第一个字,那么如何能快速查找呢?遍历吗?其显示性能太低了。解决办法其实很简单,在构造字典树的时候把下面的节点做一个排序即可。
在数据结构的排序中,对于有效列表,可以进行最快的二分查找。当然也有一些 Trie 树的变种,把这种多叉树的结构改为二叉树,其实就是为了进行天然的二分查找。还有更快的方法,就是对每一层都使用一个Hash表来存储,这样在 O(1) 的时间内就可以完成查找,但代价是占用的内存空间很大。
我们继续上面的查找,找到“中”之后开始找“中国”,“中”下面有“国”字,同时“国”字有结束标示,也就是说“中国”后面的下一个字如果不是“人”字,在 Trie 树里没找到下一个字,那么就可以结束查找而返回“中国”。但现在“中国”的后面正好是“人”字,那么能找到就继续找,因为“人”字没有结束标示,下一个字是“民”,这样就到达了树的最低层,这里的所有节点都是有结束标示的。这样就把“中国人民”分词成功,虽然它中间包含“中国”这个词,但是这个词比“中国人民”短,因此以长的词为准。
反向最大匹配
正向最大匹配只要能实现 Trie 树,剩下的部分实现起来比较容易,但错分的比例比较高。例如,“有意见分歧”“市场中国有企业才能发展”,其正向最大匹配的结果是“有意、见、分歧”和“市场、中国、有、企业、才能、发展”,显然都切分错了。正确的结果应该是“有、意见、分歧”和“市场、中、国有企业、才、能、发展”。如果使用反向最大匹配,则都可以正确切分。所谓反向最大匹配,就是把本来从左往右匹配改为从右往左匹配。也就是“中国人民”的匹配方向从“中”、“国”、“人”、“民”,改为“民”、“人”、“国”、“中”,同时为了保持字典树的结构匹配,树的顺序也改为把词的最后一个字作为第一级,把第一个字作为最后一级的叶子节点,其他使用方式全部相同。
为什么反向最大匹配比正向最大匹配更好用?这其实没有什么底层理论支撑,只是通过实验得出的结论。实验统计得出,正向最大匹配的错误率大概在 1/150,而反向最大匹配的错误率大概在 1/250,也就是说反向最大匹配并没有完全消除切分错误,只是降低了错误率。
最短路径
前面介绍的两种方法虽然可以达到一定的准确率,但也只是一种工程方法,并且未涉及机器学习算法,效果也不好。下面使用统计数据即用概率的方法来计算分词结果。所谓最短路径分词,简单地说就是把所有分词的可能性都列出来,然后寻找概率最大的那个路径。因为概率本来是相乘的,计算不方便,一般会使用 log 函数把乘法改为加法,而小于 1 的数值取对数之后会变为负数,并且所有的概率都为负,而且使用的是加法,所以不需要一直带着负号,再在取 log 的基础上取负。这样 -log 取值最小,也就是原值最大,因此叫最短路径,而不是最长路径,如下图所示。

图 2 最短路径的词网
此处大概演示一下算法的流程。以“中国人民生活”为例,先使用词表匹配分词,把所有可能的词都分出来,这里就不是最大匹配,而是全匹配,如图 2 所示。
“中国人民生活”可以分为“中”、“国”、“人”、“民”、“生”、“活”、“中国”、“国人”、“人民”、“民生”、“生活”、“中国人”等,然后可以以组成原来的句子为原则连接为一个词网。例如,“中”后面可以接“国人”,但不能接“中国”,因为这样组成的句子就成“中中国”了,同样不可以接“人民”,这样就少字了。最终连接好的词网如图 2 所示。
有了词网就可以寻找一个最优路径。那么以什么原则确定是否最优呢?也就是在词网节点之间的边上的权重使用什么值呢?一般使用的是二元词法(2-gram),这是一个统计概率。
例如“中国”后面跟“人”的概率,可以通过 count("中国人") 或 count("中国") 语句来计算。count(x) 语句的意思是语料库中词 x 的出现次数。当然有些非常少见的组合在语料库中可能没有涵盖,但不能认为其概率就是 0,还需要做平滑等操作。
有了图结构,也有了路径权重,那么求最短路径就有很多方法了,如数据结构关于图的 Dijkstra(迪杰斯特拉)算法。常用的是 Viterbi(维特比)算法,这个算法用来给 HMM(隐马尔可夫模型)算法的解码问题求解,在分词工具里分完词后还要进行基础版的命名实体识别 NER,否则遇到人名和公司名之类的词全部会被分为单字。很多工具都需要实现 HMM 算法,这样两处场景用一个算法不是更省力吗?
HMM 就是比马尔可夫模型多了一个隐藏变量的版本。正常的马尔可夫模型的逻辑是当前状态的概率基于前一个状态。例如,今天的天气依赖于昨天的天气,昨天是晴天,今天还是晴天的概率是 60%。常见的 n-gram 其实也是这个逻辑。
HMM 假设决定当前状态的是当前的隐藏状态,而当前的隐藏状态则依赖于前一个隐藏状态。例如,我们不关注天气而关注温度,那么假设温度完全是由天气决定的,那么今天的温度是多少度由今天的天气决定,而今天的天气则由前一天的天气决定,这样就形成了一个 HMM。
所谓的 Viterbi 算法,就是一个动态规划求最优解的方法。如果读者尚未学习过 HMM,看不懂这里的解释也没关系,可以把这个概念当作一个黑盒,只需要知道应该输入什么并了解输出结果表达的意思就可以了。
很多知识往往不是独立的,而是与其他知识相关联的,这时多数人喜欢把所有的知识点都弄明白,再来学习这个知识点,这也是人的天性,不过这样的学习效率不高,因为知识点的依赖有时候不像教科书那样是从前往后循序渐进排列的,这样容易导致一个知识点不懂就难以继续学习下去。如果有了黑盒思维,可以先把这个知识点封装起来,只关心其输入与输出,而不关心内部的实现,把外部的整体知识体系学明白,然后研究黑盒的内部,这样往往会起到事半功倍的效果。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: