高精度乘法详解(Java分治法实现)
设 X 和 Y 都是 n 位十进制数,要求计算它们的乘积 XY。当 n 很大时,利用传统的计算方法求 XY 时需要的计算步骤很多,运算量较大,使用分治法求解 XY 会更高效,现要求采用分治法编写一个求两个任意长度的整数相乘的算法。

图 1 大整数X和Y的分段
则:
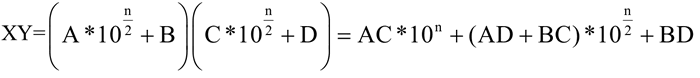
1) 若序列 a[start…end] 中只有一个元素,则最大元素和最小元素均为 a[start]。
2) 若序列 a[start…end] 中有两个元素,则最大元素为 a[start] 和 a[end] 中的较大者,最小元素为 a[start] 和 a[end] 中的较小者。
这里取的大整数 X、Y 是在理想状态下,即 X 与 Y 的位数一致,且 n=2^m,m=1,2,3,…。计算 XY 需要进行 4 次 n/2 位整数乘法运算,即 AC、AD、BC 和 BD,以及 3 次不超过 n 位的整数加法运算,此外还要进行两次移位 2^n 和 2^(n/2) 运算,这些加法运算和移位运算的时间复杂度都为 O(n)。
根据以上分析,使用分治法求解 XY 的时间复杂度为 T(n)=4T(n/2)+O(n),因此时间复杂度为 O(n^2)。
为了方便划分,当两个整数中有一个长度大于 2 时,将整数的长度扩充为 4。
当字符串长度为 2 时,结束划分,将数字字符串转换为整数进行计算:
将原来的整数 X 和 Y 分别划分为 A 和 B、C 和 D:
求解 AC、BD、(A+B)(C+D)-(AC+BD):
在 AC 后插入 n 个 0,即乘以 10^n:
在 (A+B)(C+D)-(AC+BD) 后插入 n/2 个 0,即乘以 10^(n/2):
求解 X*Y 并返回:
高精度乘法问题分析
设有两个大整数 X、Y,求 XY 就是把 X 与 Y 中的每一项相乘,但是这样的乘法效率较低。若采用分治法,则可将 X 拆分为 A 和 B,Y 拆分为 C 和 D,如下图所示。
图 1 大整数X和Y的分段
则:
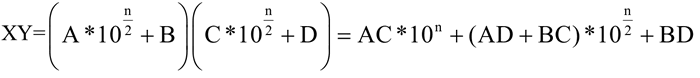
1) 若序列 a[start…end] 中只有一个元素,则最大元素和最小元素均为 a[start]。
2) 若序列 a[start…end] 中有两个元素,则最大元素为 a[start] 和 a[end] 中的较大者,最小元素为 a[start] 和 a[end] 中的较小者。
这里取的大整数 X、Y 是在理想状态下,即 X 与 Y 的位数一致,且 n=2^m,m=1,2,3,…。计算 XY 需要进行 4 次 n/2 位整数乘法运算,即 AC、AD、BC 和 BD,以及 3 次不超过 n 位的整数加法运算,此外还要进行两次移位 2^n 和 2^(n/2) 运算,这些加法运算和移位运算的时间复杂度都为 O(n)。
根据以上分析,使用分治法求解 XY 的时间复杂度为 T(n)=4T(n/2)+O(n),因此时间复杂度为 O(n^2)。
分治法实现高精度乘法
算法实现如下:
import java.util.Scanner;
public class BigUIntegerMul {
void AddZero(StringBuilder s, int n, boolean pre) {
String temp = new String();
for (int i = 0; i < n; i++) {
temp += "0";
}
if (pre) {
s.insert(0, temp);
} else {
s.append(temp);
}
}
void RemoveZero(StringBuilder str) {
int i = 0;
while (i < str.length() && str.charAt(i) == '0') {
i++;
}
if (i < str.length()) {
str.delete(0, i);
} else {
str = new StringBuilder("0");
}
}
StringBuilder BigUIntegerAdd(StringBuilder x, StringBuilder y) {
StringBuilder result = new StringBuilder();
int t, m, i, size, b;
RemoveZero(x);
RemoveZero(y);
x.reverse();
y.reverse();
m = Integer.max(x.length(), y.length());
for (i = 0, size = 0; size != 0 || i < m; i++) {
t = size;
if (i < x.length()) {
t += Integer.parseInt(String.valueOf(x.charAt(i)));
}
if (i < y.length()) {
t += Integer.parseInt(String.valueOf(y.charAt(i)));
}
b = t % 10;
result = new StringBuilder(String.valueOf(b) + result);
size = t / 10;
}
return result;
}
StringBuilder BigUIntegerSub(StringBuilder x, StringBuilder y) {
int xi, yi, i, x_size, y_size;
int[] p;
int count = 0;
StringBuilder result = new StringBuilder();
String result1 = new String();
RemoveZero(x);
RemoveZero(y);
x.reverse();
y.reverse();
x_size = x.length();
y_size = y.length();
p = new int[x_size];
for (i = 0; i < x_size; i++) {
xi = Integer.parseInt(String.valueOf(x.charAt(i)));
yi = i < y_size ? Integer.parseInt(String.valueOf(y.charAt(i))) : 0;
p[count++] = xi - yi;
}
for (i = 0; i < x_size; i++) {
if (p[i] < 0) {
p[i] += 10;
p[i + 1]--;
}
}
for (i = x_size - 1; i >= 0; i--) {
result1 += String.valueOf(p[i]);
}
result = new StringBuilder(result1);
return result;
}
StringBuilder GetBigIntegerMul(StringBuilder X, StringBuilder Y) {
String A, B, C, D;
StringBuilder result, v0, v1, v2;
int n = 2, iValue;
if (X.length() > 2 || Y.length() > 2) {
n = 4;
while (n < X.length() || n < Y.length()) {
n *= 2;
}
AddZero(X, n - X.length(), true);
AddZero(Y, n - Y.length(), true);
}
if (X.length() == 1) {
AddZero(X, 1, true);
}
if (Y.length() == 1) {
AddZero(Y, 1, true);
}
if (n == 2) {
iValue = Integer.parseInt(X.toString()) * Integer.parseInt(Y.toString());
result = new StringBuilder(String.valueOf(iValue));
} else {
A = X.substring(0, n / 2);
B = X.substring(n / 2);
C = Y.substring(0, n / 2);
D = Y.substring(n / 2);
v2 = GetBigIntegerMul(new StringBuilder(A), new StringBuilder(C));
v0 = GetBigIntegerMul(new StringBuilder(B), new StringBuilder(D));
StringBuilder BA = BigUIntegerAdd(new StringBuilder(B), new StringBuilder(A));
StringBuilder DC = BigUIntegerAdd(new StringBuilder(D), new StringBuilder(C));
StringBuilder v2v0 = BigUIntegerAdd(new StringBuilder(v2), new StringBuilder(v0));
v1 = BigUIntegerSub(GetBigIntegerMul(BA, DC), v2v0);
AddZero(v2, n, false);
AddZero(v1, n / 2, false);
result = BigUIntegerAdd(BigUIntegerAdd(v2, v1), v0);
}
return result;
}
public static void main(String args[]) {
Scanner sc = new Scanner(System.in);
BigUIntegerMul BM = new BigUIntegerMul();
System.out.println("要计算两个大整数相乘吗(y/n)?");
String ch = sc.next();
while (ch.equals("y") || ch.equals("Y")) {
System.out.println("计算两个大整数相乘:");
System.out.println("请输入第1个整数:");
StringBuilder a = new StringBuilder(sc.next());
System.out.println("请输入第2个整数:");
StringBuilder b = new StringBuilder(sc.next());
System.out.println(a + "*" + b + "=" + BM.GetBigIntegerMul(a, b));
System.out.println("要继续计算两个大整数相乘吗(y/n)?");
ch = sc.next();
}
}
}
程序运行结果如下:
要计算两个大整数相乘吗(y/n)?
y
计算两个大整数相乘:
请输入第1个整数:
123
请输入第2个整数:
456
123*456=56088
要继续计算两个大整数相乘吗(y/n)?
y
计算两个大整数相乘:
请输入第1个整数:
12345678
请输入第2个整数:
987654321
12345678*987654321=12193262222374638
要继续计算两个大整数相乘吗(y/n)?
n
为了方便划分,当两个整数中有一个长度大于 2 时,将整数的长度扩充为 4。
if (X.length() > 2 || Y.length() > 2) {
n = 4;
while (n < X.length() || n < Y.length()) {
n *= 2;
}
}
为扩充长度后的字符串添加字符 0:
AddZero(X, n - (int)X.length(),true); AddZero(Y, n - (int)Y.length(),true);
当字符串长度为 2 时,结束划分,将数字字符串转换为整数进行计算:
if (n == 2) // 递归出口
{
iValue = Integer.parseInt(X.toString()) * Integer.parseInt(Y.toString());
result = new StringBuilder(String.valueOf(iValue));
}
将原来的整数 X 和 Y 分别划分为 A 和 B、C 和 D:
A = X.substring(0, n / 2); B = X.substring(n / 2); C = Y.substring(0, n / 2); D = Y.substring(n / 2);
求解 AC、BD、(A+B)(C+D)-(AC+BD):
v2 = GetBigIntegerMul(new StringBuilder(A), new StringBuilder(C)); v0 = GetBigIntegerMul(new StringBuilder(B), new StringBuilder(D)); StringBuilder BA = BigIntegerAdd(new StringBuilder(B), new StringBuilder(A)); StringBuilder DC = BigIntegerAdd(new StringBuilder(D), new StringBuilder(C)); StringBuilder v2v0 = BigIntegerAdd(new StringBuilder(v2), new StringBuilder(v0)); v1 = BigIntegerSub(GetBigIntegerMul(BA, DC), v2v0);
在 AC 后插入 n 个 0,即乘以 10^n:
AddZero(v2, n, false);
在 (A+B)(C+D)-(AC+BD) 后插入 n/2 个 0,即乘以 10^(n/2):
AddZero(v1, n / 2, false);
求解 X*Y 并返回:
result = BigIntegerAdd(BigIntegerAdd(v2, v1), v0);
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: