高斯混合模型(附带实例,Python实现)
高斯混合模型(GMM)是一种软聚类模型。GMM 也可以看作是 k 均值的推广,因为 GMM 不仅是考虑到了数据分布的均值,也考虑到了协方差。和 k 均值一样,GMM 需要提前确定簇的个数。
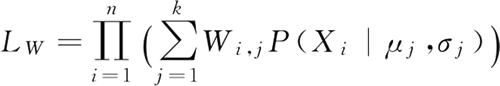
其中,P(Xi|μj, σj) 是样本 Xi 在第 j 个高斯分布中的概率密度函数。以一维高斯分布为例:
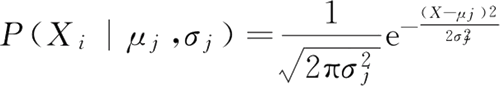
然后重复进行以上两个步骤,直到达到迭代终止条件。
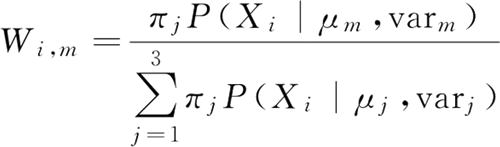
根据 W,就可以更新每一簇的占比 πm:
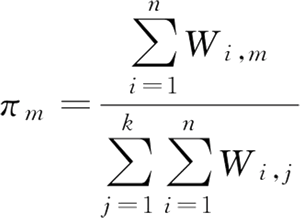
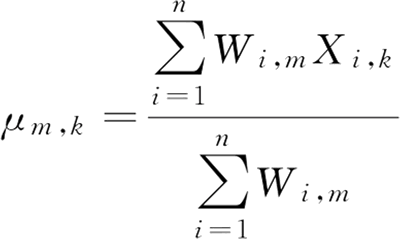
第 m 簇的第 k 个分量的方差为:
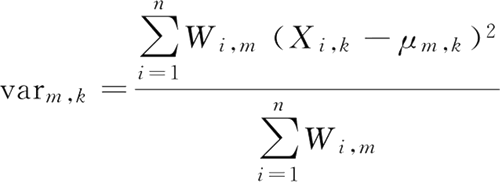
【实例】利用高斯混合模型对 iris 数据集进行聚类。
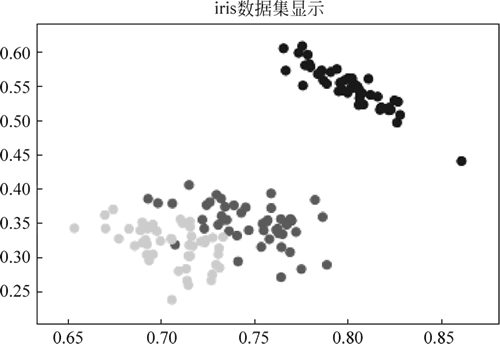
图 1 iris数据集显示
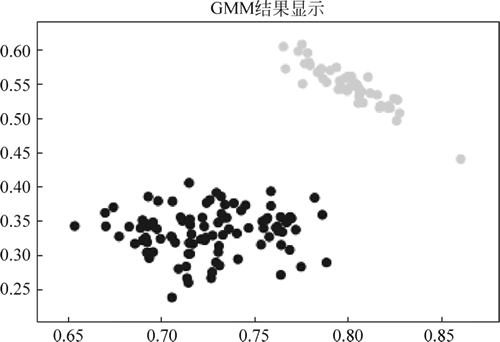
图 2 GMM显示效果
高斯混合模型概述
在高斯混合模型中,需要估计每一个高斯分布的均值与方差。从最大似然估计的角度来说,给定某个有 n 个样本的数据集 X,假如已知 GMM 中一共有 k 簇,我们就是要找到 k 组均值 μ1,…,μk,k 组方程 σ1,…,σk 来最大化以下似然函数 L:L((μ1, …, μk), (σ1, …, σk);X)将其改成:
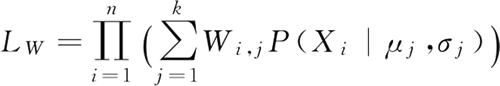
其中,P(Xi|μj, σj) 是样本 Xi 在第 j 个高斯分布中的概率密度函数。以一维高斯分布为例:
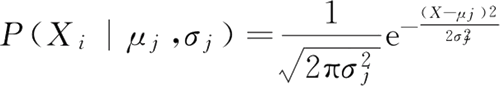
最大期望算法
有了隐变量还不够,我们还需要一个算法来找到最佳的 W,从而得到 GMM 的模型参数。最大期望算法(expectation-maximization,简称 EM)就是这样一个算法,简单说来,EM 算法分两个步骤:- 第一个步骤是 E(期望)步;
- 第二个步骤是 M(最大化)步。
然后重复进行以上两个步骤,直到达到迭代终止条件。
1) E步骤
E 步骤中,主要目的是更新 W。第 i 个变量属于第 m 簇的概率: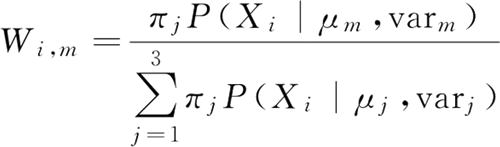
根据 W,就可以更新每一簇的占比 πm:
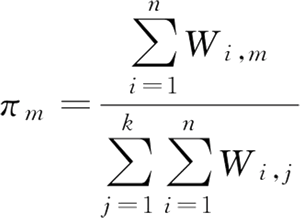
2) M步骤
M 步骤中,需要根据 E 步骤得到的 W 更新均值 μ 和方差 var。μ 和 var 分别是 W 的权重的样本 X 的均值和方差。第 m 簇的第 k 个分量的均值为: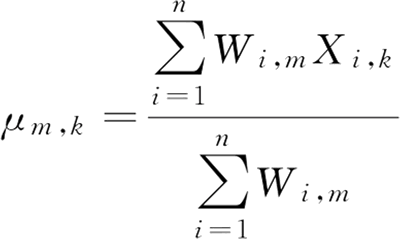
第 m 簇的第 k 个分量的方差为:
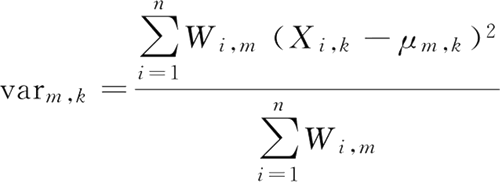
高斯混合模型实战
前面已介绍了高斯混合模型的概念、最大期望算法等相关内容,下面通过实例来演示高斯混合模型的实战。【实例】利用高斯混合模型对 iris 数据集进行聚类。
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import Normalizer
from sklearn.metrics import accuracy_score
class GMM:
def __init__(self, Data, K, weights=None, means=None, covars=None):
"""
初始化
:param Data: 训练数据
:param K: 高斯分布的个数
:param weights: 每个高斯分布的初始概率(权重)
:param means: 高斯分布的均值向量
:param covars: 高斯分布的协方差矩阵集合
"""
self.Data = Data
self.K = K
if weights is not None:
self.weights = weights
else:
self.weights = np.random.rand(self.K)
self.weights /= np.sum(self.weights) # 归一化
col = np.shape(self.Data)[1]
if means is not None:
self.means = means
else:
self.means = []
for i in range(self.K):
mean = np.random.rand(col)
self.means.append(mean)
if covars is not None:
self.covars = covars
else:
self.covars = []
for i in range(self.K):
cov = np.random.rand(col, col)
self.covars.append(cov) # cov 是 np.array,但是 self.covars 是 list
def Gaussian(self, x, mean, cov):
"""
自定义的高斯分布概率密度函数
:param x: 输入数据
:param mean: 均值数组
:param cov: 协方差矩阵
:return: x 的概率
"""
dim = np.shape(cov)[0]
covdet = np.linalg.det(cov + np.eye(dim) * 0.001)
covinv = np.linalg.inv(cov + np.eye(dim) * 0.001)
xdiff = (x - mean).reshape((1, dim))
prob = 1.0 / (np.power(np.power(2 * np.pi, dim) * np.abs(covdet), 0.5)) * \
np.exp(-0.5 * xdiff.dot(covinv).dot(xdiff.T))[0][0]
return prob
def GMM_EM(self):
"""
利用 EM 算法进行优化 GMM 参数的函数
:return: 返回各组数据的属于每个分类的概率
"""
loglikelihood = 0
oldloglikelihood = 1
len, dim = np.shape(self.Data)
gammas = [np.zeros(self.K) for i in range(len)] # gammas 表示第 n 个样本属于第 k 个混合高斯的概率
while np.abs(loglikelihood - oldloglikelihood) > 0.0000001:
oldloglikelihood = loglikelihood
# E 步骤
for n in range(len):
respons = [self.weights[k] * self.Gaussian(self.Data[n], self.means[k], self.covars[k]) for k in range(self.K)]
respons = np.array(respons)
sum_respons = np.sum(respons)
gammas[n] = respons / sum_respons
# M 步骤
for k in range(self.K):
nk = np.sum([gammas[n][k] for n in range(len)])
self.weights[k] = 1.0 * nk / len # 更新每个高斯分布的概率
self.means[k] = (1.0 / nk) * np.sum([gammas[n][k] * self.Data[n] for n in range(len)], axis=0) # 更新高斯分布的均值
xdiffs = self.Data - self.means[k]
self.covars[k] = (1.0 / nk) * np.sum([gammas[n][k] * xdiffs[n].reshape((dim, 1)).dot(xdiffs[n].reshape((1, dim))) for n in range(len)], axis=0) # 更新高斯分布的协方差矩阵
loglikelihood = []
for n in range(len):
tmp = [self.weights[k] * self.Gaussian(self.Data[n], self.means[k], self.covars[k]) for k in range(self.K)]
tmp = np.log(np.array(tmp))
loglikelihood.append(list(tmp))
loglikelihood = np.sum(loglikelihood)
for i in range(len):
gammas[i] = gammas[i] / np.sum(gammas[i])
self.posibility = gammas
self.prediction = [np.argmax(gammas[i]) for i in range(len)]
def run_main():
"""
主函数
"""
# 导入 iris 数据集
iris = load_iris()
label = np.array(iris.target)
data = np.array(iris.data)
print("iris 数据集的标签:\n", label)
# 对数据进行预处理
data = Normalizer().fit_transform(data)
# 解决图中中文乱码问题
mpl.rcParams['font.sans-serif'] = [u'simHei']
mpl.rcParams['axes.unicode_minus'] = False
# 数据可视化
plt.scatter(data[:, 0], data[:, 1], c=label)
plt.title("iris 数据集显示")
plt.show()
# GMM 模型
K = 3
gmm = GMM(data, K)
gmm.GMM_EM()
y_pre = gmm.prediction
print("GMM 预测结果:\n", y_pre)
print("GMM 正确率为:\n", accuracy_score(label, y_pre))
plt.scatter(data[:, 0], data[:, 1], c=y_pre)
plt.title("GMM 结果显示")
plt.show()
if __name__ == '__main__':
run_main()
运行程序,输出如下:
iris数据集的标签: [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2] GMM预测结果: [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] GMM正确率为: 0.6666666666666效果如图 1 及图 2 所示:

图 1 iris数据集显示

图 2 GMM显示效果
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: