高精度减法详解(C++实现,图文并茂)
在科学计算中经常会有几十位、几百位的大数,这类数被统称为“高精度数”。
高精度算法是处理高精度数的数学计算方法,它是用计算机对高精度数模拟加、减、乘、除、乘方、阶乘、开方等运算的算法。
受到存储精度的限制,在计算机中无法正常存储非常大的数。这时可以将非常大的数按照一位或者四位进行拆分,将其存储在一个数组中,用一个数组表示这个数字。
高精度减法的原理是,以字符串的形式接收高精度数,将其转换为数字后逆序存储在数组中,从低位到高位模拟高精度减法运算。
注意,高精度减法不处理负数,因此首先要判断被减数和减数哪个大,若被减数小于减数,则交换两个数,对相减后的结果加负号。例如,求解 8-15 时,因为 8<15,所以交换两个数,计算 15-8=7,输出时加负号,8-15=-(15-8)=-7。
例如,求解 8542639-93825456,步骤如下:
1) 判断两个数的大小,因为减数大于被减数,所以交换两个数,结果加负号。
2) 将两个数分别逆序存储在数组 a[]、b[] 中:
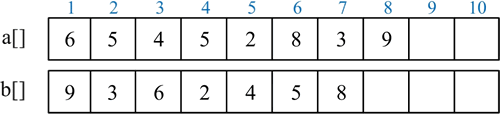
3) 从低位到高位依次处理每位数字,将结果存储在数组 c[] 中。
处理第 1 位,a[1]<b[1],向高位借 1 当 10,a[2]=a[2]-1=4,a[1]=a[1]+10=6+10=16,c[1]=a[1]-b[1]=16-9=7。

处理第 2 位,a[2]>b[2],无须借位,c[2]=a[2]-b[2]=4-3=1。
处理第 3 位,a[3]<b[3],向高位借 1 当 10,a[4]=a[4]-1=4,a[3]=a[3]+10=4+10=14,c[3]=a[3]-b[3]=14-6=8。
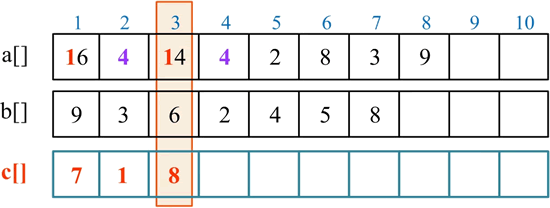
处理第 4 位,a[4]>b[4],无须借位,c[4]=a[4]-b[4]=4-2=2。
处理第 5 位,a[5]<b[5],向高位借 1 当 10,a[6]=a[6]-1=7,a[5]=a[5]+10=2+10=12,c[5]=a[5]-b[5]=12-4=8。
处理第 6 位,a[6]>b[6],无须借位,c[6]=a[6]-b[6]=7-5=2。
处理第 7 位,a[7]<b[7],向高位借 1 当 10,a[8]=a[8]-1=8,a[7]=a[7]+10=3+10=13,c[7]=a[7]-b[7]=13-8=5。
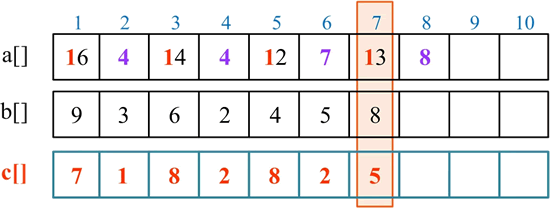
处理第 8 位,a[8]>b[8],无须借位,c[8]=a[8]-b[8]=8-0=8。
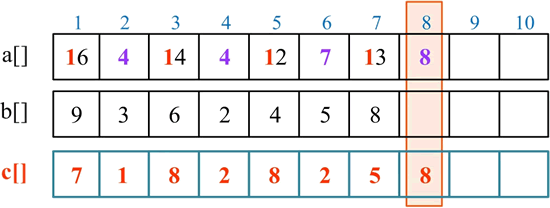
处理完毕,从高位到低位依次输出答案 -85282817,即 8542639-93825456=-85282817,注意加负号。
算法实现:
高精度算法是处理高精度数的数学计算方法,它是用计算机对高精度数模拟加、减、乘、除、乘方、阶乘、开方等运算的算法。
受到存储精度的限制,在计算机中无法正常存储非常大的数。这时可以将非常大的数按照一位或者四位进行拆分,将其存储在一个数组中,用一个数组表示这个数字。
高精度减法的原理是,以字符串的形式接收高精度数,将其转换为数字后逆序存储在数组中,从低位到高位模拟高精度减法运算。
注意,高精度减法不处理负数,因此首先要判断被减数和减数哪个大,若被减数小于减数,则交换两个数,对相减后的结果加负号。例如,求解 8-15 时,因为 8<15,所以交换两个数,计算 15-8=7,输出时加负号,8-15=-(15-8)=-7。
高精度减法对借位的处理
在进行减法运算时,从低位到高位依次处理每位数字,若被减数的当前位小于减数的当前位,则需要向高位借位,借 1 当 10。例如,求解 8542639-93825456,步骤如下:
1) 判断两个数的大小,因为减数大于被减数,所以交换两个数,结果加负号。
2) 将两个数分别逆序存储在数组 a[]、b[] 中:

3) 从低位到高位依次处理每位数字,将结果存储在数组 c[] 中。
处理第 1 位,a[1]<b[1],向高位借 1 当 10,a[2]=a[2]-1=4,a[1]=a[1]+10=6+10=16,c[1]=a[1]-b[1]=16-9=7。

处理第 2 位,a[2]>b[2],无须借位,c[2]=a[2]-b[2]=4-3=1。
处理第 3 位,a[3]<b[3],向高位借 1 当 10,a[4]=a[4]-1=4,a[3]=a[3]+10=4+10=14,c[3]=a[3]-b[3]=14-6=8。

处理第 4 位,a[4]>b[4],无须借位,c[4]=a[4]-b[4]=4-2=2。
处理第 5 位,a[5]<b[5],向高位借 1 当 10,a[6]=a[6]-1=7,a[5]=a[5]+10=2+10=12,c[5]=a[5]-b[5]=12-4=8。
处理第 6 位,a[6]>b[6],无须借位,c[6]=a[6]-b[6]=7-5=2。
处理第 7 位,a[7]<b[7],向高位借 1 当 10,a[8]=a[8]-1=8,a[7]=a[7]+10=3+10=13,c[7]=a[7]-b[7]=13-8=5。

处理第 8 位,a[8]>b[8],无须借位,c[8]=a[8]-b[8]=8-0=8。

处理完毕,从高位到低位依次输出答案 -85282817,即 8542639-93825456=-85282817,注意加负号。
高精度减法的具体实现
算法设计:- 比较两个数的大小,若被减数小于减数,则交换两个数,结果加负号。
- 以字符串的形式接收高精度数,将其转换为数字后逆序存储在数组中。
- 从低位到高位模拟高精度减法运算,若被减数的当前位小于减数的当前位,则向高位借位,借 1 当 10。
- 减法运算结果的最大长度为两个数的长度最大值,有可能高位出现多个前导 0,需要先删除前导 0,然后从高位到低位依次输出答案,要特别注意结果是否有负号。例如,8542639-8542533=0000106,需要删除前导 0,输出答案 106。
算法实现:
#include <iostream>
using namespace std;
const int maxn=10500;
int a[maxn], b[maxn], c[maxn];
int main() {
string s1, s2;
cin >> s1 >> s2;
// 先比较两个数的大小
if (s1.size() <= s2.size() || (s1.size() == s2.size() && s1 < s2)) {
swap(s1, s2); // 交换,例如,8-15 = (15-8)
cout << "-"; // 输出负号
}
int n = s1.length();
int m = s2.length();
int len = max(n, m);
for (int i = 0; i < n; i++) // 将第1个字符串存储在数组中,逆序存储
a[n - i] = s1[i] - '0';
for (int i = 0; i < m; i++) // 将第2个字符串存储在数组中,逆序存储
b[m - i] = s2[i] - '0';
for (int i = 1; i <= len; i++) { // 高精度加法
if (a[i] < b[i]) { // 向高位借1
a[i + 1]--; // 高位减1
a[i] += 10; // 借1当10
}
c[i] = a[i] - b[i]; // 减法
}
while (c[len] == 0 && len > 1) len--; // 删除前导 0
for (int i = len; i > 0; i--) // 从高位到低位依次输出答案
cout << c[i];
return 0;
}
运行结果为:
8542639 93825456
-85282817
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: