高精度乘法详解(C++实现,图文并茂)
在科学计算中经常会有几十位、几百位的大数,这类数被统称为“高精度数”。
高精度算法是处理高精度数的数学计算方法,它是用计算机对高精度数模拟加、减、乘、除、乘方、阶乘、开方等运算的算法。
受到存储精度的限制,在计算机中无法正常存储非常大的数。这时可以将非常大的数按照一位或者四位进行拆分,将其存储在一个数组中,用一个数组表示这个数字。
高精度乘法的原理是,以字符串的形式接收高精度数,将其转换为数字后逆序存储在数组中,从低位到高位模拟高精度乘法运算。
对于 a[i]×b[j],将其结果存储在 c[i+j-1] 的位置,还需要累加上次的结果。例如,在计算 9362×25 时,c'[4]=a[4]×b[1],c''[4]=a[3]×b[2],c[4]=c'[4]+c''[4]。
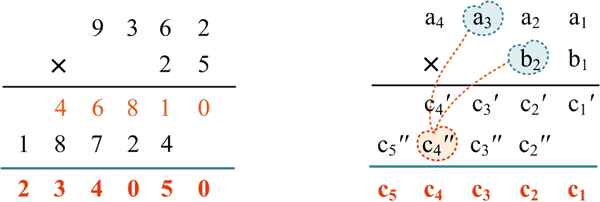
方法 1:在累加乘积的过程中处理进位。用变量 x 记录上次的进位,累加乘积 c[i+j-1]+=a[i]×b[j]+x,更新进位 x=c[i+j-1]/10,当前位 c[i+j-1]%=10。
方法 2:在累加乘积之后处理进位。两个数的每一位分别相乘,累加乘积 c[i+j-1]+=a[i]×b[j],在计算完毕后,从低位到高位开始判断,若 c[i]>9,则处理进位,c[i+1]+=c[i]/10,更新当前位c[i]%=10。
在此采用方法 2,求解 9362×25,过程如下:
1) 累加乘积:从低位到高位,两个数的每一位分别相乘,累加乘积 c[i+j-1]+=a[i]×b[j]。
2) 处理进位:从低位到高位开始判断,若 c[i]>9,则更新进位 c[i+1]+=c[i]/10,当前位 c[i]%=10:
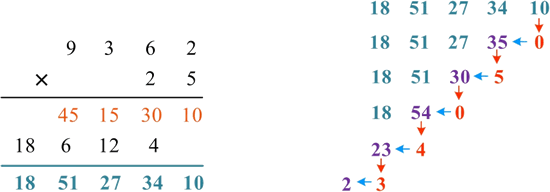
3) 处理完毕,从高位到低位依次输出答案 234050,即 9362×25=234050。
高精度算法是处理高精度数的数学计算方法,它是用计算机对高精度数模拟加、减、乘、除、乘方、阶乘、开方等运算的算法。
受到存储精度的限制,在计算机中无法正常存储非常大的数。这时可以将非常大的数按照一位或者四位进行拆分,将其存储在一个数组中,用一个数组表示这个数字。
高精度乘法的原理是,以字符串的形式接收高精度数,将其转换为数字后逆序存储在数组中,从低位到高位模拟高精度乘法运算。
高精度乘法对进位的处理
在进行乘法运算时,从低位到高位依次处理每位数字,两个数的每一位分别相乘,累加乘积,既可以在累加乘积的过程中处理进位,也可以在累加乘积之后处理进位。对于 a[i]×b[j],将其结果存储在 c[i+j-1] 的位置,还需要累加上次的结果。例如,在计算 9362×25 时,c'[4]=a[4]×b[1],c''[4]=a[3]×b[2],c[4]=c'[4]+c''[4]。
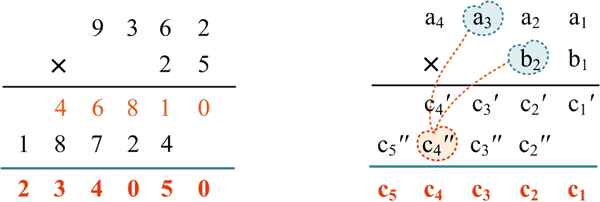
方法 1:在累加乘积的过程中处理进位。用变量 x 记录上次的进位,累加乘积 c[i+j-1]+=a[i]×b[j]+x,更新进位 x=c[i+j-1]/10,当前位 c[i+j-1]%=10。
方法 2:在累加乘积之后处理进位。两个数的每一位分别相乘,累加乘积 c[i+j-1]+=a[i]×b[j],在计算完毕后,从低位到高位开始判断,若 c[i]>9,则处理进位,c[i+1]+=c[i]/10,更新当前位c[i]%=10。
在此采用方法 2,求解 9362×25,过程如下:
1) 累加乘积:从低位到高位,两个数的每一位分别相乘,累加乘积 c[i+j-1]+=a[i]×b[j]。
2) 处理进位:从低位到高位开始判断,若 c[i]>9,则更新进位 c[i+1]+=c[i]/10,当前位 c[i]%=10:
- c[1]=10>9,处理进位,c[2]=c[2]+c[1]/10=34+1=35,当前位 c[1]=10%10=0;
- c[2]=35>9,处理进位,c[3]=c[3]+c[2]/10=27+3=30,当前位 c[2]=35%10=5;
- c[3]=30>9,处理进位,c[4]=c[4]+c[3]/10=51+3=54,当前位 c[3]=30%10=0;
- c[4]=54>9,处理进位,c[5]=c[5]+c[4]/10=18+5=23,当前位 c[4]=54%10=4;
- c[5]=23>9,处理进位,c[6]=c[6]+c[5]/10=0+2=2,当前位 c[5]=23%10=3。
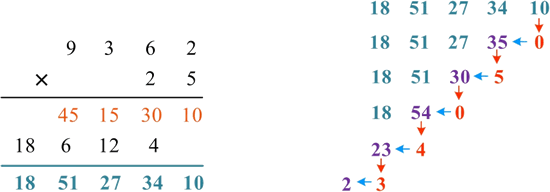
3) 处理完毕,从高位到低位依次输出答案 234050,即 9362×25=234050。
高精度乘法算法设计
- 以字符串的形式接收高精度数,将其转换为数字后逆序存储在数组中;
- 累加乘积。从低位到高位,两个数的每一位分别相乘,累加乘积 c[i+j-1]+=a[i]×b[j];
- 处理进位。从低位到高位开始判断,若 c[i]>9,则更新进位 c[i+1]+=c[i]/10,当前位 c[i]%=10;
- 乘法运算结果的最大长度为两个数的长度之和,有可能高位出现前导 0,需要先删除前导 0,然后从高位到低位依次输出答案。
高精度乘法算法实现
#include <iostream>
using namespace std;
const int maxn=40500; //注意,每个数都有2000位,乘积最多有2000*2+1位
int a[maxn], b[maxn], c[maxn];
int main() {
string s1, s2;
cin >> s1 >> s2;
int n = s1.length();
int m = s2.length();
int len = n + m;
for (int i = 0; i < n; i++) // 将第1个字符串存储在数组中,逆序存储
a[n - i] = s1[i] - '0';
for (int i = 0; i < m; i++) // 将第2个字符串存储在数组中,逆序存储
b[m - i] = s2[i] - '0';
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) // 累加乘积
c[i + j - 1] += a[i] * b[j]; // 累加乘积
for (int i = 1; i < len; i++) { // 处理进位
if (c[i] > 9) {
c[i + 1] += c[i] / 10;
c[i] %= 10;
}
}
}
while (c[len] == 0 && len > 1) len--; // 删除前导 0
for (int i = len; i > 0; i--) // 从高位到低位依次输出答案
cout << c[i];
return 0;
}
运行结果为:
9362 25
234050
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: