循环神经网络详解(Python实现)
我们见过的很多神经网络(如 NN 和 CNN)都有一个主要特点,那就是它们都没有记忆。它们单独处理每个输入,在输入与输入之间没有保存任何状态。对于这样的网络,要想处理数据点的序列或时间序列,需要向网络同时展示整个序列,即将序列转换成单个数据点,这种网络叫作前向网络(feedforward network)。
与此相反,当阅读一个句子时,我们是一个词一个词地阅读,同时会记住之前的内容。这让我们能够动态理解这个句子所传达的含义。生物智能以渐进的方式处理信息,同时保存一个关于所处理内容的模型,这个模型是根据过去的信息构建的,并随着新信息的进入而不断更新。
按照这种思想,我们又得到一种新的模型,叫作循环神经网络(recurrent neural network, RNN),该网络会遍历处理所有序列元素,并保存一个记录已查看内容相关信息的状态(state)。
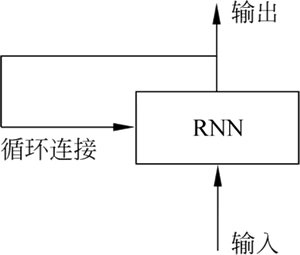
图 1 带有环的循环网络
RNN 是一类具有内部环的神经网络(见图 1)。而在处理下一条序列之时,RNN 的状态会被重置。使用 RNN 时,仍可以将一整个序列输出网络,不过在网络内部,不是直接处理整个序列数据,而是自动对序列的元素进行遍历。
为了将环和状态的概念解释清楚,用 Numpy 实现一个简单 RNN 的前向传播。该 RNN 的输入是一个张量序列,将其编码成大小为 timesteps×input_features 的二维张量。对时间步 timesteps 进行遍历,在每个时间步,考虑 t 时刻的当前状态与 t 时刻的输入,计算得到 t 时刻的输出。然后,将下一个时间步的状态设置为上一个时间步的输出。对于第一个时间步,上一个时间步的输出没有定义,所以它没有当前状态。因此,需要将状态初始化为一个全零向量,这称作网络的初始状态。
【实例 1】简单 RNN 的 Numpy 实现。
RNN 是一个 for 循环,它重复使用循环前一次迭代的计算结果,具体展开如下图所示。
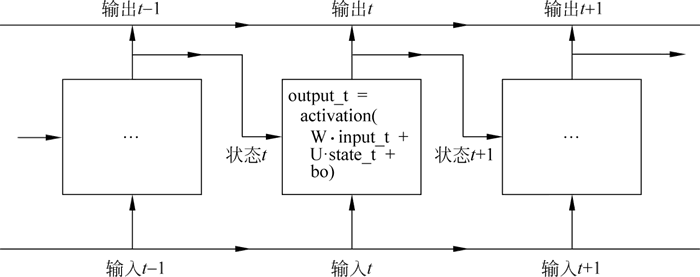
图 2 一个沿时间展开的简单RNN
与 Keras 中的所有循环层一样,SimpleRNN 可以在两种不同模式下运行:
【实例 2】Keras 中的循环层实例演示。
下面再通过一个实例来演示循环神经网络的应用。
【实例 3】构建一个简单的神经网络,网络共有三层(两个隐藏层)。
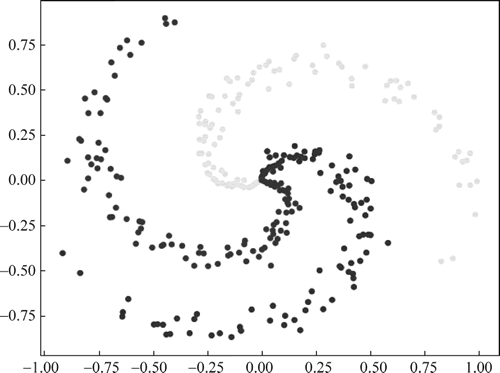
图 3 螺旋数据集
LSTM 在 SimpleRNN 的基础上,增加了一种跨越多个时间步传递信息的方法。这个新方法做的事情就像一条在序列旁边的辅助传送带,序列中的信息可以在任意位置跳上传送带,然后被传送到更晚的时间步,并在需要时原封不动地跳回来。
先从 SimpleRNN 单元开始介绍,如下图所示:
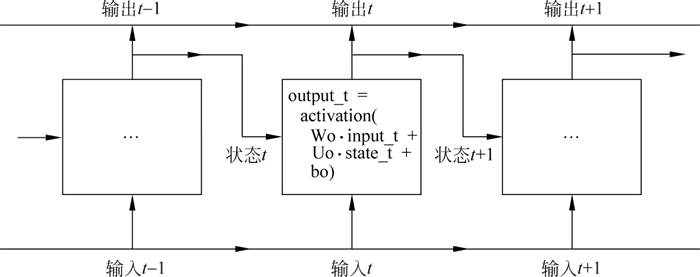
图 4 SimpleRNN单元
因为 SimpleRNN 单元有许多个权重矩阵,所以对单元中的 W 和 U 两个矩阵添加下标字母 o(Wo 和 Uo),表示输出。
然后,添加一个“携带轨道”数据流,用来携带信息跨越时间步,如下图所示:
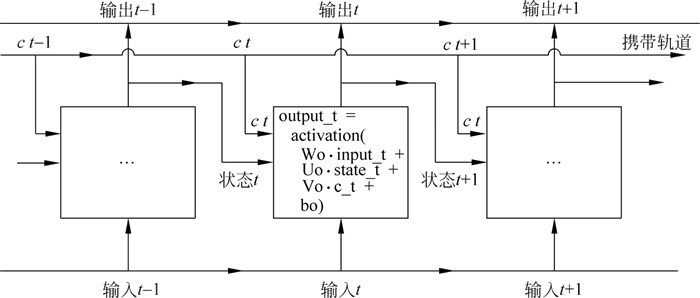
图 5 添加一个携带轨道
这个“携带轨道”上放着时间步 t 的 Ct 信息(C 表示 carry),这些信息将与输入、状态一起进行运算,从而影响传递到下一个时间步的状态:
下图给出了添加上述架构之后的图,即 LSTM 结构图:
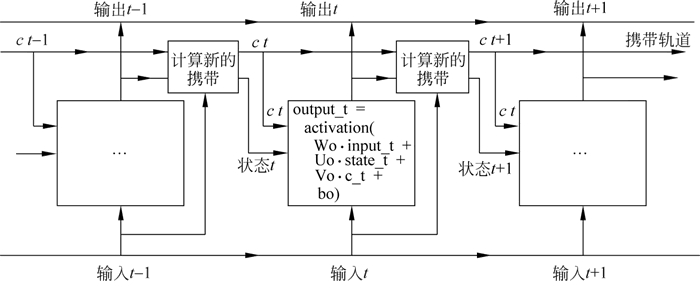
图 6 LSTM结构图
【实例 4】在 Keras 中使用 LSTM 层。使用 LSTM 层创建一个模型,然后在 IMDB 数据上训练模型。只需要指定 LSTM 层的输出维度,其他参数都是使用 Keras 默认值。Keras 具有很好的默认值,无须手动调参,模型通常也能正常运行。
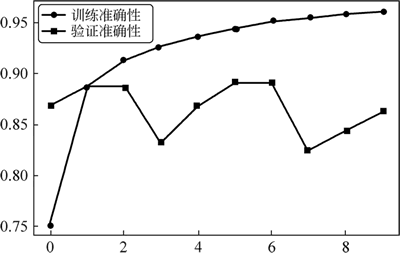
图 7 训练与验证准确性
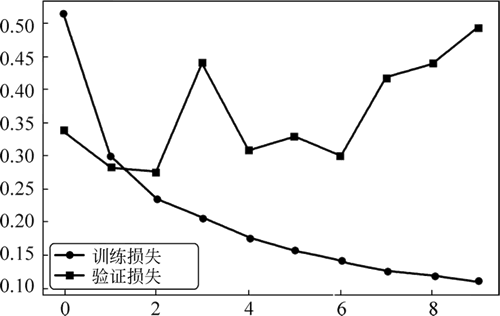
图 8 训练与验证损失
与此相反,当阅读一个句子时,我们是一个词一个词地阅读,同时会记住之前的内容。这让我们能够动态理解这个句子所传达的含义。生物智能以渐进的方式处理信息,同时保存一个关于所处理内容的模型,这个模型是根据过去的信息构建的,并随着新信息的进入而不断更新。
按照这种思想,我们又得到一种新的模型,叫作循环神经网络(recurrent neural network, RNN),该网络会遍历处理所有序列元素,并保存一个记录已查看内容相关信息的状态(state)。

图 1 带有环的循环网络
RNN 是一类具有内部环的神经网络(见图 1)。而在处理下一条序列之时,RNN 的状态会被重置。使用 RNN 时,仍可以将一整个序列输出网络,不过在网络内部,不是直接处理整个序列数据,而是自动对序列的元素进行遍历。
为了将环和状态的概念解释清楚,用 Numpy 实现一个简单 RNN 的前向传播。该 RNN 的输入是一个张量序列,将其编码成大小为 timesteps×input_features 的二维张量。对时间步 timesteps 进行遍历,在每个时间步,考虑 t 时刻的当前状态与 t 时刻的输入,计算得到 t 时刻的输出。然后,将下一个时间步的状态设置为上一个时间步的输出。对于第一个时间步,上一个时间步的输出没有定义,所以它没有当前状态。因此,需要将状态初始化为一个全零向量,这称作网络的初始状态。
【实例 1】简单 RNN 的 Numpy 实现。
import numpy as np
#输入序列的时间步数
timesteps = 100
#输入特征空间的维度
input_features = 32
#输出特征空间的维度
output_features = 64
#输入数据:随机噪声
inputs = np.random.random((timesteps,input_features))
#初始状态:全零向量
state_t = np.zeros((output_features))
#创建随机的权重矩阵
U = np.random.random((output_features,output_features))
W = np.random.random((output_features,input_features))
b = np.random.random((output_features,))
successive_outputs = []
for input_t in inputs:#input_t是形状为(input_features,)的向量
#由输入和当前状态(前一个输出)计算得到当前输出
output_t = np.tanh(np.dot(W,input_t) + np.dot(U,state_t) + b)
#将这个输出保存到一个列表中
successive_outputs.append(output_t)
state_t = output_t
#最终输出是一个形状为(timesteps,output_features)的二维张量
final_output_sequence = np.stack(successive_outputs,axis = 0)
print('形状为(timesteps,output_features)的二维张量:\n',successive_outputs[2])
运行程序,输出如下:
形状为(timesteps,output_features)的二维张量: [1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]以上结果中,最终输出是一个形状为(timesteps,output_features)的二维张量,是所有 timesteps 的结果拼起来的。但实际上,一般只用最后一个结果 successive_outputs[-1] 就可以了,这个里面已经包含了之前所有步骤的结果,即包含了整个序列的信息。
RNN 是一个 for 循环,它重复使用循环前一次迭代的计算结果,具体展开如下图所示。

图 2 一个沿时间展开的简单RNN
Keras中的循环层
实例 1 的简单实现,实际对应一个 Keras 层,即 SimpleRNN 层,导入该层的方法为:from tensorflow.keras.layers import SimpleRNN二者有微小的区别:SimpleRNN 层能够像其他 Keras 层一样处理序列批量,而不是像实例 1(Numpy 实例)那样只能处理单个序列。因此,它接收形状为(batch_size,timesteps,input_features)的输入,而不是(timesteps,input_features)。
与 Keras 中的所有循环层一样,SimpleRNN 可以在两种不同模式下运行:
- 一种是返回每个时间步连续输出的完整序列,即形状为(batch_size,timesteps,output_features)的三维张量;
- 另一种是只返回每个输入序列的最终输出,即形状为(batch_size,output_features)的二维张量。这两种模式由 return_sequences 这个构造函数参数来控制。
【实例 2】Keras 中的循环层实例演示。
# 只返回最后一个时间步的输出 from tensorflow.keras.models import Sequential from tensorflow.keras.layers import Embedding, SimpleRNN model = Sequential() model.add(Embedding(10000, 32)) model.add(SimpleRNN(32)) model.summary() Model: "sequential" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= embedding (Embedding) (None, None, 32) 320000 _________________________________________________________________ simple_rnn (SimpleRNN) (None, 32) 2080 ================================================================= Total params: 322,080 Trainable params: 322,080 Non-trainable params: 0 _________________________________________________________________ # 返回完整的状态序列 model = Sequential() model.add(Embedding(10000, 32)) model.add(SimpleRNN(32, return_sequences=True)) model.summary() Model: "sequential_2" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= embedding_2 (Embedding) (None, None, 32) 320000 _________________________________________________________________ simple_rnn_2 (SimpleRNN) (None, None, 32) 2080 ================================================================= Total params: 322,080 Trainable params: 322,080 Non-trainable params: 0 ================================================================= 为了提高网络的表示能力,有时会将多个循环层逐个堆叠。在这种情况下,需要让所有中间层都返回完整的输出序列: # 堆叠多个 RNN 层,中间层返回完整的输出序列 model = Sequential() model.add(Embedding(10000, 32)) model.add(SimpleRNN(32, return_sequences = True)) model.add(SimpleRNN(32, return_sequences = True)) model.add(SimpleRNN(32, return_sequences = True)) model.add(SimpleRNN(32)) # 最后一层要最后一个输出就行了 model.summary() Model: "sequential_3" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= embedding_3 (Embedding) (None, None, 32) 320000 _________________________________________________________________ simple_rnn_3 (SimpleRNN) (None, None, 32) 2080 _________________________________________________________________ simple_rnn_4 (SimpleRNN) (None, None, 32) 2080 _________________________________________________________________ simple_rnn_5 (SimpleRNN) (None, None, 32) 2080 _________________________________________________________________ simple_rnn_6 (SimpleRNN) (None, 32) 2080 ================================================================= Total params: 328,320 Trainable params: 328,320 Non-trainable params: 0 =================================================================
下面再通过一个实例来演示循环神经网络的应用。
【实例 3】构建一个简单的神经网络,网络共有三层(两个隐藏层)。
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
x = 1/(1 + np.exp(-x))
return x
def sigmoid_grad(x):
return (x) * (1 - x)
# RELU 函数(max(0, x))不会随输入大小而饱和
def relu(x):
return np.maximum(0, x)
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# 构成一个不易线性分离的分类数据集
# 玩具螺旋数据由三个类别(蓝色,红色,黄色)组成,这些类别不是线性可分的
N = 100 # 每个类的点数
D = 2 # 维度
K = 3 # 类的数量
X = np.zeros((N * K, D))
y = np.zeros(N * K, dtype='uint8')
for j in range(K):
ix = range(N * j, N * (j + 1))
r = np.linspace(0.0, 1, N) # 半径
t = np.linspace(j * 4, (j + 1) * 4, N) + np.random.randn(N) * 0.2 # θ
X[ix] = np.c_[r * np.sin(t), r * np.cos(t)]
y[ix] = j
# 可视化数据:
plt.scatter(X[:, 0], X[:, 1], c = y, s = 40, cmap = plt.cm.Spectral)
plt.show()
# 定义 relu 和 sigmoid 函数
# 构建一个非常简单的神经网络,有三层(两个隐藏层)
def three_layer_net(NONLINEARITY, X, y, model, step_size, reg):
# NONLINEARITY: 表示使用哪种激活函数
# 初始化参数
h = model['h']
h2 = model['h2']
W1 = model['W1']
W2 = model['W2']
W3 = model['W3']
b1 = model['b1']
b2 = model['b2']
b3 = model['b3']
# 梯度下降
num_examples = X.shape[0]
plot_array_1 = []
plot_array_2 = []
for i in range(50000):
# 前向传播
if NONLINEARITY == 'RELU':
hidden_layer = relu(np.dot(X, W1) + b1)
hidden_layer2 = relu(np.dot(hidden_layer, W2) + b2)
scores = np.dot(hidden_layer2, W3) + b3
elif NONLINEARITY == 'SIGM':
hidden_layer = sigmoid(np.dot(X, W1) + b1)
hidden_layer2 = sigmoid(np.dot(hidden_layer, W2) + b2)
scores = np.dot(hidden_layer2, W3) + b3
# 计算损失
# probs 为 300 × 3 的数组,其中每行现在包含了概率
exp_scores = np.exp(scores)
probs = exp_scores / np.sum(exp_scores, axis = 1, keepdims = True) # [N × K]
# correct_logprobs 是一维数组,仅包含为每个示例分配给正确类的概率
# 完全损失就是这些对数概率和正则化损失的平均值
correct_logprobs = - np.log(probs[range(num_examples), y])
data_loss = np.sum(correct_logprobs)/num_examples
reg_loss = 0.5 * reg * np.sum(W1**2) + 0.5 * reg * np.sum(W2**2) + 0.5 * reg * np.sum(W3**2)
loss = data_loss + reg_loss
if i % 1000 == 0:
print("迭代 %d: 损失 %f" % (i, loss))
# 计算分数的梯度
dscores = probs
dscores[range(num_examples), y] -= 1
dscores /= num_examples
dW3 = (hidden_layer2.T).dot(dscores)
db3 = np.sum(dscores, axis = 0, keepdims = True)
if NONLINEARITY == 'RELU':
# 反向传播 RELU 非线性
dhidden2 = np.dot(dscores, W3.T)
dhidden2[hidden_layer2 <= 0] = 0
dw2 = np.dot(hidden_layer.T, dhidden2)
plot_array_2.append(np.sum(np.abs(dw2))/np.sum(np.abs(dw2.shape)))
db2 = np.sum(dhidden2, axis = 0)
dhidden = np.dot(dhidden2, W2.T)
dhidden[hidden_layer <= 0] = 0
dw1 = np.dot(X.T, dhidden)
plot_array_1.append(np.sum(np.abs(dw1))/np.sum(np.abs(dw1.shape)))
db1 = np.sum(dhidden, axis = 0)
elif NONLINEARITY == 'SIGM':
# 反向传播 sigmoid 非线性
dhidden2 = dscores.dot(W3.T) * sigmoid_grad(hidden_layer2)
dw2 = (hidden_layer.T).dot(dhidden2)
plot_array_2.append(np.sum(np.abs(dw2))/np.sum(np.abs(dw2.shape)))
db2 = np.sum(dhidden2, axis = 0)
dhidden = dhidden2.dot(W2.T) * sigmoid_grad(hidden_layer)
dw1 = np.dot(X.T, dhidden)
plot_array_1.append(np.sum(np.abs(dw1))/np.sum(np.abs(dw1.shape)))
db1 = np.sum(dhidden, axis = 0)
# 添加正则化
dW3 += reg * W3
dw2 += reg * W2
dw1 += reg * W1
# 返回损失的选项
grads = {}
grads['W1'] = dw1
grads['W2'] = dw2
grads['W3'] = dw3
grads['b1'] = db1
grads['b2'] = db2
grads['b3'] = db3
# 返回 loss, grads
return loss, grads
# 更新
W1 += - step_size * dw1
b1 += - step_size * db1
W2 += - step_size * dw2
b2 += - step_size * db2
W3 += - step_size * dw3
b3 += - step_size * db3
# 评估训练集的准确性
if NONLINEARITY == 'RELU':
hidden_layer = relu(np.dot(X, W1) + b1)
hidden_layer2 = relu(np.dot(hidden_layer, W2) + b2)
scores = np.dot(hidden_layer2, W3) + b3
elif NONLINEARITY == 'SIGM':
hidden_layer = sigmoid(np.dot(X, W1) + b1)
hidden_layer2 = sigmoid(np.dot(hidden_layer, W2) + b2)
scores = np.dot(hidden_layer2, W3) + b3
predicted_class = np.argmax(scores, axis = 1)
print('训练准确性: %.2f' % (np.mean(predicted_class == y)))
# 返回 cost, grads
return plot_array_1, plot_array_2, W1, W2, W3, b1, b2, b3
# 用 sigmoid 非线性训练网络
N = 100 # 每个类的点数
D = 2 # 维度
K = 3 # 类数量
h = 50 # 隐藏层 1 的大小
h2 = 50 # 隐藏层 2 的大小
# 用 ReLU 非线性训练网络
model = {}
model['h'] = h
model['h2'] = h2
model['W1'] = 0.1 * np.random.randn(D, h)
model['b1'] = np.zeros((1, h))
model['W2'] = 0.1 * np.random.randn(h, h2)
model['b2'] = np.zeros((1, h2))
model['W3'] = 0.1 * np.random.randn(h2, K)
model['b3'] = np.zeros((1, K))
(relu_array_1, relu_array_2, r_W1, r_W2, r_W3, r_b1, r_b2, r_b3) = three_layer_net('RELU', X, y, model, step_size=1e-1, reg=1e-3)
运行程序,输出如下:
迭代0:损失1.110276
迭代1000:损失0.328156
迭代2000:损失0.160904
迭代3000:损失0.136820
迭代4000:损失0.130236
迭代5000:损失0.127130
…
迭代45000:损失0.110563
迭代46000:损失0.110425
迭代47000:损失0.110294
迭代48000:损失0.110165
迭代49000:损失0.110011
训练准确性:0.99

图 3 螺旋数据集
LSTM层和GRU层
SimpleRNN 并不是 Keras 中唯一可用的循环层,还有另外两个:LSTM 和 GRU。在实践中总会用到其中之一,因为 SimpleRNN 通常过于简化,没有实用的价值。SimpleRNN 的最大问题是:在时刻 t,理论上来说,它应该能够记住许多时间步之前见过的信息,但实际上它是不可能学到这种长期依赖的。其原因在于梯度消失问题,它类似于在层数较多的非循环网络(前向网络)中观察到的效应:随着层数的增加,网络最终变得无法训练。LSTM 层和 GRU 层都是为了解决这个问题而设计的。1) LSTM层
LSTM 层是基于 LSTM(long short-term memory,长短期记忆)算法的,该算法就是专门研究处理梯度消失问题的。其核心思想是要保存信息以便后面使用,防止前面得到的信息在后面的处理中逐渐消失。LSTM 在 SimpleRNN 的基础上,增加了一种跨越多个时间步传递信息的方法。这个新方法做的事情就像一条在序列旁边的辅助传送带,序列中的信息可以在任意位置跳上传送带,然后被传送到更晚的时间步,并在需要时原封不动地跳回来。
先从 SimpleRNN 单元开始介绍,如下图所示:

图 4 SimpleRNN单元
因为 SimpleRNN 单元有许多个权重矩阵,所以对单元中的 W 和 U 两个矩阵添加下标字母 o(Wo 和 Uo),表示输出。
然后,添加一个“携带轨道”数据流,用来携带信息跨越时间步,如下图所示:

图 5 添加一个携带轨道
这个“携带轨道”上放着时间步 t 的 Ct 信息(C 表示 carry),这些信息将与输入、状态一起进行运算,从而影响传递到下一个时间步的状态:
output_t = activation(dot(state_t, Uo) + dot(input_t, Wo) + dot(C_t,Vo) + bo) i_t = activation(dot(state_t, Ui) + dot(input_t, Wi) + bi) f_t = activation(dot(state_t, Uf) + dot(input_t, Wf) + bf) k_t = activation(dot(state_t, Uk) + dot(input_t, Wk) + bk) c_t_next = i_t * k_t + c_t * f_t从概念上来看,“携带轨道”数据流是一种调节下一个输出和下一个状态的方法。
下图给出了添加上述架构之后的图,即 LSTM 结构图:

图 6 LSTM结构图
【实例 4】在 Keras 中使用 LSTM 层。使用 LSTM 层创建一个模型,然后在 IMDB 数据上训练模型。只需要指定 LSTM 层的输出维度,其他参数都是使用 Keras 默认值。Keras 具有很好的默认值,无须手动调参,模型通常也能正常运行。
from tensorflow.keras.layers import LSTM
model = Sequential()
model.add(Embedding(max_features, 32))
model.add(LSTM(32))
model.add(Dense(1, activation='sigmoid'))
model.summary()
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['acc'])
history = model.fit(input_train, y_train,
epochs=10,
batch_size=128,
validation_split=0.2)
model.summary()
Model: "sequential_5"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
embedding_5 (Embedding) (None, None, 32) 320000
_________________________________________________________________
lstm (LSTM) (None, 32) 8320
_________________________________________________________________
dense_1 (Dense) (None, 1) 33
=================================================================
Total params: 328,353
Trainable params: 328,353
Non-trainable params: 0
_________________________________________________________________
Epoch 1/10
157/157 [==============================] - 37s 236ms/step - loss: 0.5143 - acc: 0.7509 - val_loss: 0.3383 - val_acc: 0.8672
...
Epoch 10/10
157/157 [==============================] - 34s 217ms/step - loss: 0.1113 - acc: 0.9615 - val_loss: 0.4926 - val_acc: 0.8614
# 绘制结果
import matplotlib.pyplot as plt
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'bo-', label='训练准确性')
plt.plot(epochs, val_acc, 'rs-', label='验证准确性')
plt.legend()
plt.figure()
plt.plot(epochs, loss, 'bo-', label='训练损失')
plt.plot(epochs, val_loss, 'rs-', label='验证损失')
plt.legend()
plt.show()
运行程序,效果如图 7 和图 8 所示。
图 7 训练与验证准确性

图 8 训练与验证损失
2) GRU层
GRU 是 LSTM 的简化,运算代价更低。GRU 层的简单使用示例如下:
model = Sequential()
model.add(layers.GRU(32, input_shape = (None, float_data.shape[-1])))
model.add(layers.Dense(1))
model.compile(optimizer = RMSprop(), loss = 'mae')
history = model.fit_generator(train_gen,
steps_per_epoch = 500,
epochs = 20,
validation_data = val_gen,
validation_steps = val_steps)
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: