RNN循环神经网络详解(新手必看)
神经网络有多种,而 RNN 在序列数据(如时间序列或自然语言)建模方面非常强大,很适合用于时间序列建模。那么 RNN 是如何做到这一点的呢?
我们从 RNN 的原理说起。简单来说,RNN 层会使用 for 循环对序列的时间步骤进行迭代,同时维持一个内部状态,对截至目前所看到的时间步骤信息进行编码。这个原理表示,其他神经网络是假设所有输入和输出都彼此独立,而 RNN 的输出取决于先前的计算。
RNN 可以捕获到目前为止计算的信息。理论上,RNN 可以利用任意长度序列中的信息,虽然实际上这个长度并不长。这种特性称为“记忆”。
为了让大家有个感性的认识,我们通过图 1 展示 RNN 与前馈神经网络的对比情况:
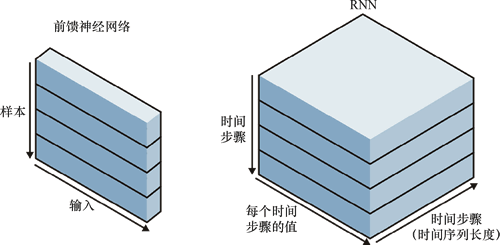
图 1 RNN与前馈神经网络的对比情况
我们可以看到左侧的前馈神经网络与时间序列长度没有关系,而右侧的 RNN 则多了一个概念:时间步骤(数量为时间序列长度)。这样输入不仅和当前时刻的输入相关,也与其过去一段时间的输出相关。
接下来,我们讲解具体代码实现。我们将使用 Keras 来构建 RNN:
然后,通过 SimpleRNN 类构建 RNN(In [3])。可以看到我们输入了多个参数:
激活函数在隐藏层中引入非线性,以便我们能够对非线性问题进行建模。如果不用激活函数,每一层输出都将是上一层输入的线性函数。这样的话,无论神经网络有多少层,输出都是输入的线性组合,与没有隐藏层效果一样。
常见的激活函数如下:
1) sigmoid:这个激活函数允许我们在模型中引入小的变化时合并少量的输出。它的取值范围为(0,1)。sigmoid 函数的数学表达式为:
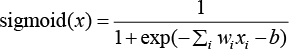
其中,w 表示权重,x 表示数据,b 表示偏差,下标 i 表示特征。
2) tanh:如果要处理的是负数,tanh 函数适合。与 sigmoid 函数不同,它的取值范围为(−1,1)。tanh 函数的公式为:
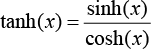
3) linear:使用 linear 函数可以在自变量和因变量之间建立线性关系。线性激活函数的形式为:
4) Rectified Linear Unit:简称 ReLU,即在代码中先输入的 relu。如果输入为 0 或小于 0,则取 0。如果大于 0,则按照以下公式取值:
5) softmax:与 sigmoid 函数一样,这个激活函数也广泛适用于分类问题,因为 softmax 函数将输入转换成与输入数的指数成正比的概率分布。softmax 函数的公式为:
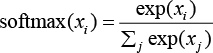
return_sequences 参数表示是返回输出序列中的最后一个输出,还是全部序列。我们设置为 True,表示返回全部序列。
看完知识点之后,来看看以下具体的实现代码:
配置好模型及变量之后,我们开始提取 Apple 公司和 Microsoft 公司的股价数据并进行预测:
然后,使用以下代码可视化结果:
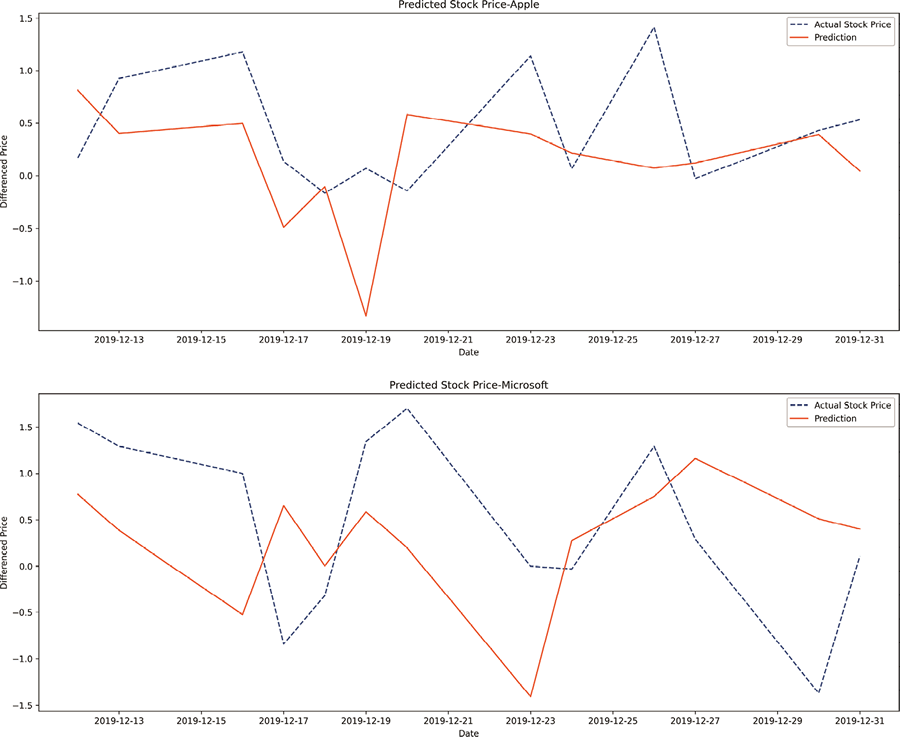
图 5 RNN 模型预测结果
即使改进之后得到令人满意的预测性能,RNN 模型的缺点也不容忽视。RNN 的主要缺点如下:
在设计不当的深度学习场景中,梯度消失是一个很常见的问题。当进行反向传播时,如果梯度变小,就会出现梯度消失问题。这意味着神经元学习速度太慢,以致优化过程陷入停顿。
梯度爆炸是指当进行反向传播时,反向传播的微小变化导致网络权重的大幅更新。梯度消失或梯度爆炸在原理上是相似的。
我们从 RNN 的原理说起。简单来说,RNN 层会使用 for 循环对序列的时间步骤进行迭代,同时维持一个内部状态,对截至目前所看到的时间步骤信息进行编码。这个原理表示,其他神经网络是假设所有输入和输出都彼此独立,而 RNN 的输出取决于先前的计算。
RNN 可以捕获到目前为止计算的信息。理论上,RNN 可以利用任意长度序列中的信息,虽然实际上这个长度并不长。这种特性称为“记忆”。
为了让大家有个感性的认识,我们通过图 1 展示 RNN 与前馈神经网络的对比情况:

图 1 RNN与前馈神经网络的对比情况
我们可以看到左侧的前馈神经网络与时间序列长度没有关系,而右侧的 RNN 则多了一个概念:时间步骤(数量为时间序列长度)。这样输入不仅和当前时刻的输入相关,也与其过去一段时间的输出相关。
接下来,我们讲解具体代码实现。我们将使用 Keras 来构建 RNN:
- 我们先设置前面提到的时间步骤,即 n_steps = 13(In [2])。
- 设置特征数为 1,即 n_features = 1(In [2])。
- Keras 有两种构建模型的方法:Sequential models 和 Functional API。这里选择 Sequential models方法(In [3] 的 model = Sequential())。
然后,通过 SimpleRNN 类构建 RNN(In [3])。可以看到我们输入了多个参数:
- 第一个参数表示神经元的数量,设置为 512。
- 第二个参数 activation 表示激活函数,这里选择了“relu”。下面详细讲解激活函数。
激活函数
激活函数是用来确定神经网络结构输出的数学方程。激活函数在隐藏层中引入非线性,以便我们能够对非线性问题进行建模。如果不用激活函数,每一层输出都将是上一层输入的线性函数。这样的话,无论神经网络有多少层,输出都是输入的线性组合,与没有隐藏层效果一样。
常见的激活函数如下:
1) sigmoid:这个激活函数允许我们在模型中引入小的变化时合并少量的输出。它的取值范围为(0,1)。sigmoid 函数的数学表达式为:
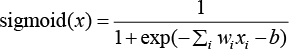
其中,w 表示权重,x 表示数据,b 表示偏差,下标 i 表示特征。
2) tanh:如果要处理的是负数,tanh 函数适合。与 sigmoid 函数不同,它的取值范围为(−1,1)。tanh 函数的公式为:
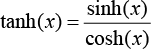
3) linear:使用 linear 函数可以在自变量和因变量之间建立线性关系。线性激活函数的形式为:
f(x) = wx
4) Rectified Linear Unit:简称 ReLU,即在代码中先输入的 relu。如果输入为 0 或小于 0,则取 0。如果大于 0,则按照以下公式取值:
ReLU(x) = max(0, x)
5) softmax:与 sigmoid 函数一样,这个激活函数也广泛适用于分类问题,因为 softmax 函数将输入转换成与输入数的指数成正比的概率分布。softmax 函数的公式为:
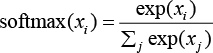
return_sequences 参数表示是返回输出序列中的最后一个输出,还是全部序列。我们设置为 True,表示返回全部序列。
看完知识点之后,来看看以下具体的实现代码:
In [1]: import numpy as np
import pandas as pd
import math
import datetime
import yfinance as yf
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.callbacks import EarlyStopping
from tensorflow.keras.layers import (Dense, Dropout,
Activation, Flatten,
MaxPooling2D, SimpleRNN)
from sklearn.model_selection import train_test_split
In [2]: n_steps = 13 ❶
n_features = 1 ❷
In [3]: model = Sequential() ❸
model.add(SimpleRNN(512, activation='relu',
input_shape=(n_steps, n_features),
return_sequences=True)) ❹
model.add(Dropout(0.2)) ❺
model.add(Dense(256, activation = 'relu')) ❻
model.add(Flatten()) ❼
model.add(Dense(1, activation='linear')) ❽
In [4]: model.compile(optimizer='rmsprop',
loss='mean_squared_error',
metrics=['mse']) ❾
In [5]: def split_sequence(sequence, n_steps):
X, y = [], []
for i in range(len(sequence)):
end_ix = i + n_steps
if end_ix > len(sequence) - 1:
break
seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]
X.append(seq_x)
y.append(seq_y)
return np.array(X), np.array(y) ❿
- ❶:定义时间步骤。
- ❷:定义特征数。
- ❸:选择 Sequential models 方法来构建模型。
- ❹:构建 SimpleRNN。
- ❺:添加 dropout 层以防止过拟合。
- ❻:添加一个具有 256 个神经元、使用 ReLU 激活函数的隐藏层。
- ❼:将模型展平以将三维矩阵转换为向量。
- ❽:添加一个输出层,激活函数设置为 linear。
- ❾:编译 RNN 模型。
- ❿:创建自变量 X 和因变量 y。
配置好模型及变量之后,我们开始提取 Apple 公司和 Microsoft 公司的股价数据并进行预测:
In [6]: ticker = ['AAPL', 'MSFT']
start = datetime.datetime(2019, 1, 1)
end = datetime.datetime(2020, 1 ,1)
stock_prices = yf.download(ticker,start=start, end = end, interval='1d')\
.Close
[*********************100%***********************] 2 of 2 completed
In [7]: diff_stock_prices = stock_prices.diff().dropna()
In [8]: split = int(len(diff_stock_prices['AAPL'].values) * 0.95)
diff_train_aapl = diff_stock_prices['AAPL'].iloc[:split]
diff_test_aapl = diff_stock_prices['AAPL'].iloc[split:]
diff_train_msft = diff_stock_prices['MSFT'].iloc[:split]
diff_test_msft = diff_stock_prices['MSFT'].iloc[split:]
In [9]: X_aapl, y_aapl = split_sequence(diff_train_aapl, n_steps) ❶
X_aapl = X_aapl.reshape((X_aapl.shape[0], X_aapl.shape[1],
n_features)) ❷
In [10]: history = model.fit(X_aapl, y_aapl,
epochs=400, batch_size=150, verbose=0,
validation_split = 0.10) ❸
In [11]: start = X_aapl[X_aapl.shape[0] - n_steps] ❹
x_input = start ❺
x_input = x_input.reshape((1, n_steps, n_features))
In [12]: tempList_aapl = [] ❻
for i in range(len(diff_test_aapl)):
x_input = x_input.reshape((1, n_steps, n_features)) ❼
yhat = model.predict(x_input, verbose=0) ❽
x_input = np.append(x_input, yhat)
x_input = x_input[1:]
tempList_aapl.append(yhat) ❾
In [13]: X_msft, y_msft = split_sequence(diff_train_msft, n_steps)
X_msft = X_msft.reshape((X_msft.shape[0], X_msft.shape[1],
n_features))
In [14]: history = model.fit(X_msft, y_msft,
epochs=400, batch_size=150, verbose=0,
validation_split = 0.10)
In [15]: start = X_msft[X_msft.shape[0] - n_steps]
x_input = start
x_input = x_input.reshape((1, n_steps, n_features))
In [16]: tempList_msft = []
for i in range(len(diff_test_msft)):
x_input = x_input.reshape((1, n_steps, n_features))
yhat = model.predict(x_input, verbose=0)
x_input = np.append(x_input, yhat)
x_input = x_input[1:]
tempList_msft.append(yhat)
- ❶:调用 split_sequence 函数定义回溯期。
- ❷ 将训练集数据重塑成三维形式的。
- ❸ 使用 RNN 模型拟合 Apple 公司股价。
- ❹ 定义 Apple 公司股价预测的起点。
- ❺ 重命名变量。
- ❻ 创建空列表以存储预测值。
- ❼ 重塑 x_input,用于预测。
- ❽ 预测 Apple 公司股价。
- ❾ 将 yhat 值存储到 tempList_aapl 列表中。
然后,使用以下代码可视化结果:
In [17]: fig, ax = plt.subplots(2,1, figsize=(18,15))
ax[0].plot(diff_test_aapl, label='Actual Stock Price', linestyle='--')
ax[0].plot(diff_test_aapl.index, np.array(tempList_aapl).flatten(),
linestyle='solid', label="Prediction")
ax[0].set_title('Predicted Stock Price-Apple')
ax[0].legend(loc='best')
ax[1].plot(diff_test_msft, label='Actual Stock Price', linestyle='--')
ax[1].plot(diff_test_msft.index,np.array(tempList_msft).flatten(),
linestyle='solid', label="Prediction")
ax[1].set_title('Predicted Stock Price-Microsoft')
ax[1].legend(loc='best')
for ax in ax.flat:
ax.set(xlabel='Date', ylabel='Differenced Price')
plt.show()
最终输出下图所示的图表。只要仔细观察一下就可以看到,模型的预测性能还有改进的空间。
图 5 RNN 模型预测结果
即使改进之后得到令人满意的预测性能,RNN 模型的缺点也不容忽视。RNN 的主要缺点如下:
- 存在梯度消失或梯度爆炸问题。
- 训练一个 RNN 是一项非常困难的任务,因为需要大量的数据。
- 当使用 tanh 激活函数时,RNN 无法处理很长的序列。
在设计不当的深度学习场景中,梯度消失是一个很常见的问题。当进行反向传播时,如果梯度变小,就会出现梯度消失问题。这意味着神经元学习速度太慢,以致优化过程陷入停顿。
梯度爆炸是指当进行反向传播时,反向传播的微小变化导致网络权重的大幅更新。梯度消失或梯度爆炸在原理上是相似的。
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: