MATLAB limit()求极限函数的用法(附带实例)
微分学中的基本概念是导数与微分,其中导数是曲线切线的斜率,反映函数相对于自变量变化的速度;而微分则表明当自变量有微小变化时函数大体上变化多少。积分是微分的逆运算。
微积分中导数的定义是通过极限给出的,即极限概念是数学分析或高等数学中最基本的概念,所以极限运算就是微积分运算的前提与基础。
在 MATLAB 中,利用 limit() 函数可以求符号表达式的极限,其调用格式如下:
【实例 1】试证明:
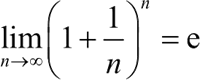
和
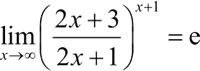
1) 在命令行窗口中输入以下语句,并查看输出结果:
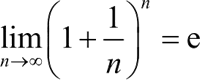
2) 在命令行窗口中输入以下语句,并查看输出结果:
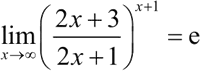
【实例 2】试求:
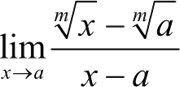
与:
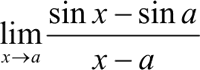
1) 在命令行窗口中输入以下语句,并查看输出结果:
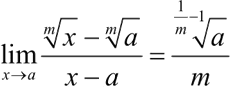
2) 在命令行窗口中输入以下语句,并查看输出结果:
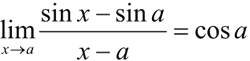
微积分中导数的定义是通过极限给出的,即极限概念是数学分析或高等数学中最基本的概念,所以极限运算就是微积分运算的前提与基础。
在 MATLAB 中,利用 limit() 函数可以求符号表达式的极限,其调用格式如下:
limit(f,x,a) % 计算符号表达式 f 当变量 x→a 时的极限值 limit(f,a) % 计算符号表达式 f 中由函数 symvar 返回的独立变量趋向于 a 时的极限值 limit(f) % 计算符号表达式 f 当 x→0 时的极限值 limit(f,x,a,'right') % 计算符号表达式 f 在 x→a (从右趋向于 a) 时的极限值 limit(f,x,a,'left') % 计算符号表达式 f 在 x→a (从左趋向于 a) 时的极限值
【实例 1】试证明:
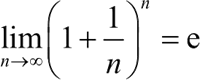
和
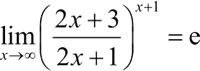
1) 在命令行窗口中输入以下语句,并查看输出结果:
>> syms n
>> limit((1+(1/n))^n,n,inf)
ans =
exp(1)
得证: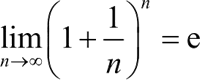
2) 在命令行窗口中输入以下语句,并查看输出结果:
>> syms x
>> limit(((2*x+3)/(2*x+1))^(x+1),x,inf)
ans =
exp(1)
得证: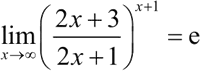
【实例 2】试求:
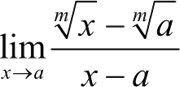
与:
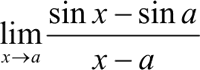
1) 在命令行窗口中输入以下语句,并查看输出结果:
>> syms x m a
>> limit(((x^(1/m)-a^(1/m))/(x-a)),a)
ans =
a^(1/m-1)/m
得证: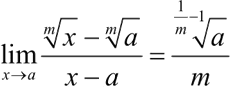
2) 在命令行窗口中输入以下语句,并查看输出结果:
>> syms x a
>> limit(((sin(x)-sin(a))/(x-a)),a)
ans =
cos(a)
得证: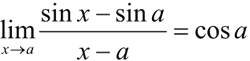
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: