MATLAB求矩阵的逆
对于 n 阶方阵 A,如果有 n 阶方阵 B 满足 AB=BA=I,则称方阵 A 为可逆的,称方阵 B 为 A 的逆矩阵,记为 A-1。
满足 |A|≠0 的方阵 A 称为非奇异的,否则就称为奇异的。
求解矩阵的逆使用函数 inv,调用格式为:
【实例】求解矩阵的逆。在 MATLAB 命令行窗口中输入以下命令:
注意,逆矩阵必须使用方阵,即 2×2、3×3,即 n×n 格式的矩阵,否则弹出警告信息。例如:
【实例】求下列矩阵的逆矩阵与转置矩阵。
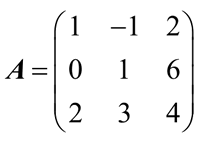
在 MATLAB 命令行窗口中输入以下命令:
【实例】验证逆矩阵性质 (λA)-1=λ-1A-1。在 MATLAB 命令行窗口中输入以下命令:
1、可逆矩阵的性质
一般地,可逆矩阵具有如下性质:- 若 A 可逆,则 A−1 是唯一的。
- 若 A 可逆,则 A−1 也可逆,并且 (A-1)-1=A。
- 若 n 阶方阵 A 与 B 都可逆,则 AB 也可逆,且 (AB)-1=B-1A-1。
- 若 A 可逆,则 |A-1|=|A|-1。
满足 |A|≠0 的方阵 A 称为非奇异的,否则就称为奇异的。
求解矩阵的逆使用函数 inv,调用格式为:
Y=inv(X)
【实例】求解矩阵的逆。在 MATLAB 命令行窗口中输入以下命令:
>> clear % 清除工作区的变量
>> A=rand(3) % 创建一个3×3的随机数矩阵A
A =
0.0540 0.9340 0.4694
0.5308 0.1299 0.0119
0.7792 0.5688 0.3371
>> B = inv(A) % 求矩阵A的逆矩阵
B =
-0.5946 0.7689 0.8008
4.7250 4.5818 -3.9912
-3.2235 -14.1952 7.8498
注意,逆矩阵必须使用方阵,即 2×2、3×3,即 n×n 格式的矩阵,否则弹出警告信息。例如:
>> A=[1 -1;0 1;2 3]; % 创建3×2的矩阵A >> B=inv(A) % 求矩阵A的逆矩阵 错误使用 inv 矩阵必须为方阵
2、矩阵的求逆条件数运算
求解矩阵的逆条件数值使用函数 rcond,调用格式为C=rcond(A)【实例】求解矩阵的逆条件数。在 MATLAB 命令行窗口中输入以下命令:
>> clear % 清除工作区的变量
>> A=rand(3) % 创建一个3×3的随机数矩阵A
A =
0.0540 0.9340 0.4694
0.5308 0.1299 0.0119
0.7792 0.5688 0.3371
>> C = rcond(A) % 求矩阵A的逆条件数
C =
0.0349
【实例】求下列矩阵的逆矩阵与转置矩阵。
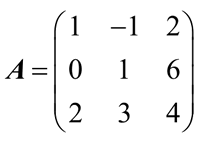
在 MATLAB 命令行窗口中输入以下命令:
>> clear % 清除工作区的变量
>> A=[1 -1 2;0 1 6;2 3 4] % 输入矩阵A
A =
1 -1 2
0 1 6
2 3 4
>> B=inv(A) % 求矩阵A的逆矩阵
B =
0.4667 -0.3333 0.2667
-0.4000 0 0.2000
0.0667 0.1667 -0.0333
>> C=A' % 求矩阵A的转置矩阵
C =
1 0 2
-1 1 3
2 6 4
【实例】验证逆矩阵性质 (λA)-1=λ-1A-1。在 MATLAB 命令行窗口中输入以下命令:
>> clear % 清除工作区的变量
>> A=[1,-1,2;0,1,6;2,3,4]; % 创建一个3×3的方阵A
>> A1=6*A % 计算6与矩阵A的乘积
A1 =
6 -6 12
0 6 36
12 18 24
>> B1=6*inv(A) % 计算6与矩阵A的逆矩阵的乘积
B1 =
2.8000 -2.0000 1.6000
-2.4000 0 1.2000
0.4000 1.0000 -0.2000
>> B2=inv(6)*inv(A) % 计算6的倒数与A的逆矩阵的乘积
B2 =
0.0778 -0.0556 0.0444
-0.0667 0 0.0333
0.0111 0.0278 -0.0056
>> B3=inv(A1) % 计算6与矩阵A的乘积的逆矩阵
B3 =
0.0778 -0.0556 0.0444
-0.0667 0 0.0333
0.0111 0.0278 -0.0056
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: