一文彻底了解神经网络(新手必看)
神经网络的概念最初来源于生物学家对大脑神经网络的研究,从中发现其神经元的工作原理,从数学角度提出感知器模型,并对其进行抽象化。
在神经网络中,神经元处理单元可以表示不同的对象,例如特征、字母、概念,或者一些有意义的抽象模式。网络中处理单元的类型分为三类,分别是输入单元、输出单元和隐单元:
神经元间的连接权值反映了单元间的连接强度,信息的表示和处理体现在网络处理单元的连接关系中。
神经网络是一种模仿生物神经网络的结构和功能的数学模型或计算模型,它是由大量的节点(即神经元)和其间的相互连接构成的,每个节点代表一种特定的输出函数,称为激励函数,每两个节点间的连接都代表一个通过该连接信号的加权值,称之为权重。
神经元是神经网络的基本元素,如下图所示:
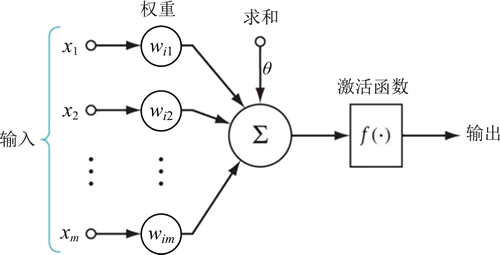
图 1 神经元
其中, x1,…,xm 是从其他神经元传来的输入信号,wij 表示从神经元 j 到神经元 i 的连接权值,θ 表示一个阈值,或称为偏置,则神经元 i 的输出与输入的关系表示为:
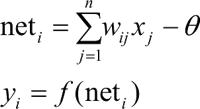
其中,yi 表示神经元 i 的输出,函数 f 称为激活函数,neti 称为净激活。若将阈值看成神经元 i 的一个输入 x0 的权重 wi0,则上面的式子可以简化为:
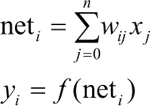
若用 X 表示输入向量,用 W 表示权重向量,即:
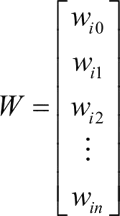
则神经元的输出可以表示为向量相乘的形式:
MLP 可以认为是一个有向图,由多个节点层组成,每一层全连接到下一层。除输入节点外,每个节点都是一个带有非线性激活函数的神经元(或称处理单元)。
多层感知机由以下几个部分组成:
多层感知机模型如下图所示:
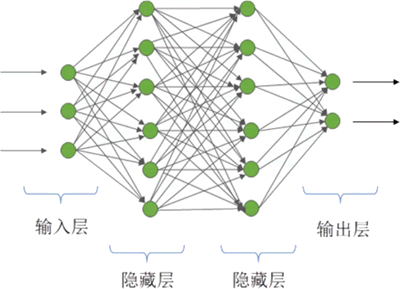
图 5 多层感知机模型
多层感知机通过在训练过程中不断调整连接权重和偏置来学习输入数据中的模式。这种调整通常是通过反向传播算法实现的,该算法利用输出误差来更新网络中的权重,以减少预测错误。
MLP 是感知机的推广,克服了感知机不能对线性不可分数据进行识别的弱点。若每个神经元的激活函数都是线性函数,那么任意层数的MLP都可以被简化成一个等价的单层感知机。
MLP 本身可以使用任何形式的激活函数,譬如阶梯函数或逻辑 S 形函数(Logistic Sigmoid Function),但为了使用反向传播算法进行有效学习,激活函数必须限制为可微函数。由于具有良好的可微性,很多 S 形函数,尤其是双曲正切(Hyperbolic Tangent)函数及逻辑 S 形函数,被采用为激活函数。
常被 MLP 用来进行学习的反向传播算法,在模式识别领域已经成为标准的监督学习算法,并在计算神经学及并行分布式处理领域中获得广泛研究。MLP 已被证明是一种通用的函数近似方法,可以被用来拟合复杂的函数,或解决分类问题。
隐藏层神经元的作用是从样本中提取样本数据中的内在规律模式并保存起来,隐藏层每个神经元与输入层都有边相连,隐藏层将输入数据加权求和并通过非线性映射作为输出层的输入,通过对输入层的组合加权及映射找出输入数据的相关模式,而且这个过程是通过误差反向传播自动完成的。
当隐藏层节点太少的时候,能够提取以及保存的模式较少,获得的模式不足以概括样本的所有有效信息,得不到样本的特定规律,导致识别同样模式新样本的能力较差,学习能力较差。
当隐藏层节点个数过多时,学习时间变长,神经网络的学习能力较强,能学习较多输入数据之间的隐含模式,但是一般来说输入数据之间与输出数据相关的模式个数未知,当学习能力过强时,有可能把训练输入样本与输出数据无关的非规律性模式学习进来,而这些非规律性模式往往大部分是样本噪声,这种情况叫作过拟合(Over Fitting)。
过拟合是记住了过多和特定样本相关的信息,当新来的样本含有相关模式但是很多细节并不相同时,预测性能并不是太好,降低了泛化能力。这种情况的表现往往是在训练数据集上误差极小,在测试数据集上误差较大。
具体隐藏层神经元个数的多少取决于样本中蕴含规律的个数以及复杂程度,而样本蕴含规律的个数往往和样本数量有关系。确定网络隐藏层参数的一个办法是将隐藏层个数设置为超参,使用验证集验证,选择在验证集中误差最小的作为神经网络的隐藏层节点个数。还有就是通过简单的经验设置公式来确定隐藏层神经元个数:
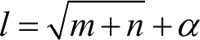
其中,l 为隐藏层节点个数,m 是输入层节点个数,n 是输出层节点个数,α 一般是 1~10 的常数。
MLP 在 20 世纪 80 年代的时候曾是相当流行的机器学习方法,拥有广泛的应用场景,譬如语音识别、图像识别、机器翻译等,但自 20 世纪 90 年代以来,MLP 遇到来自更为简单的支持向量机的强劲竞争。由于深度学习的成功,MLP 又重新得到了关注。
在前馈神经网络(Feedforward Neural Network,FNN)中,每一层的神经元可以接收前一层神经元的信号,并产生信号输出到下一层。整个网络中无反馈,信号从输入层向输出层单向传播。
前馈神经网络通过下面的公式进行信息传播:
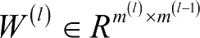 表示第 l-1 层到第 l 层的权重矩阵。
表示第 l-1 层到第 l 层的权重矩阵。
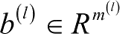 表示第 l-1 层到第 l 层的偏置。
表示第 l-1 层到第 l 层的偏置。
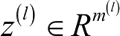 表示第 l 层神经元的净输入。
表示第 l 层神经元的净输入。
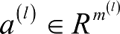 表示第 l 层神经元的输出。
表示第 l 层神经元的输出。
这样前馈神经网络通过逐层的信息传递,得到网络最后的输出。整个网络可以看作一个复合函数,将向量 X 作为第 1 层的输入 a(0),将第 L 层的输出 a(L) 作为整个函数的输出。
神经元模型
神经元模型是 1943 年由心理学家 Warren McCulloch 和数理逻辑学家 Walter Pitts 在合作的 a logical calculus of the ideas immanent in nervous activity 论文中提出的,并给出了人工神经网络的概念及人工神经元的数学模型,从而开创了人工神经网络研究的时代。在神经网络中,神经元处理单元可以表示不同的对象,例如特征、字母、概念,或者一些有意义的抽象模式。网络中处理单元的类型分为三类,分别是输入单元、输出单元和隐单元:
- 输入单元接收外部世界的信号与数据;
- 输出单元实现系统处理结果的输出;
- 隐单元是处在输入和输出单元之间,不能由系统外部观察的单元。
神经元间的连接权值反映了单元间的连接强度,信息的表示和处理体现在网络处理单元的连接关系中。
神经网络是一种模仿生物神经网络的结构和功能的数学模型或计算模型,它是由大量的节点(即神经元)和其间的相互连接构成的,每个节点代表一种特定的输出函数,称为激励函数,每两个节点间的连接都代表一个通过该连接信号的加权值,称之为权重。
神经元是神经网络的基本元素,如下图所示:

图 1 神经元
其中, x1,…,xm 是从其他神经元传来的输入信号,wij 表示从神经元 j 到神经元 i 的连接权值,θ 表示一个阈值,或称为偏置,则神经元 i 的输出与输入的关系表示为:
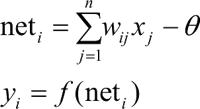
其中,yi 表示神经元 i 的输出,函数 f 称为激活函数,neti 称为净激活。若将阈值看成神经元 i 的一个输入 x0 的权重 wi0,则上面的式子可以简化为:
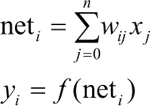
若用 X 表示输入向量,用 W 表示权重向量,即:
X=[x0, x1,…,xn ]
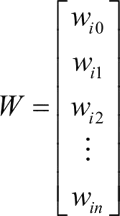
则神经元的输出可以表示为向量相乘的形式:
neti =XW yi =f(neti)=f(XW)如果神经元的净激活为正,则称该神经元处于激活状态或兴奋状态,如果神经元的净激活为负,则称神经元处于抑制状态。
多层感知机
多层感知机(Multi-Layer Perceptron,MLP)是一种前向结构的人工神经网络,用于映射一组输入向量到一组输出向量。MLP 可以认为是一个有向图,由多个节点层组成,每一层全连接到下一层。除输入节点外,每个节点都是一个带有非线性激活函数的神经元(或称处理单元)。
多层感知机由以下几个部分组成:
- 输入层:接收外部信息,并将这些信息传递到网络中。输入层中的节点并不进行任何计算,它们只是将数据分布到下一层的神经元。
- 隐藏层:一个或多个隐藏层位于输入层和输出层之间。每个隐藏层都包含若干神经元,这些神经元具有非线性激活函数,如 Sigmoid 或 Tanh 函数。隐藏层的神经元与前一层的所有神经元全连接,并且它们的输出会作为信号传递到下一层。
- 输出层:输出层产生网络的最终输出,用于进行预测或分类。输出层神经元的数量取决于要解决的问题类型,例如在二分类问题中通常只有一个输出神经元,而在多分类问题中则可能有多个输出神经元。
- 权重和偏置:连接两个神经元的权重表示这两个神经元之间联系的强度。每个神经元还有一个偏置项,它帮助调整神经元激活的难易程度。
- 激活函数:激活函数引入非线性因素,使得神经网络能够学习和模拟更复杂的关系。没有激活函数的神经网络将无法解决线性不可分的问题。
多层感知机模型如下图所示:

图 5 多层感知机模型
多层感知机通过在训练过程中不断调整连接权重和偏置来学习输入数据中的模式。这种调整通常是通过反向传播算法实现的,该算法利用输出误差来更新网络中的权重,以减少预测错误。
MLP 是感知机的推广,克服了感知机不能对线性不可分数据进行识别的弱点。若每个神经元的激活函数都是线性函数,那么任意层数的MLP都可以被简化成一个等价的单层感知机。
MLP 本身可以使用任何形式的激活函数,譬如阶梯函数或逻辑 S 形函数(Logistic Sigmoid Function),但为了使用反向传播算法进行有效学习,激活函数必须限制为可微函数。由于具有良好的可微性,很多 S 形函数,尤其是双曲正切(Hyperbolic Tangent)函数及逻辑 S 形函数,被采用为激活函数。
常被 MLP 用来进行学习的反向传播算法,在模式识别领域已经成为标准的监督学习算法,并在计算神经学及并行分布式处理领域中获得广泛研究。MLP 已被证明是一种通用的函数近似方法,可以被用来拟合复杂的函数,或解决分类问题。
隐藏层神经元的作用是从样本中提取样本数据中的内在规律模式并保存起来,隐藏层每个神经元与输入层都有边相连,隐藏层将输入数据加权求和并通过非线性映射作为输出层的输入,通过对输入层的组合加权及映射找出输入数据的相关模式,而且这个过程是通过误差反向传播自动完成的。
当隐藏层节点太少的时候,能够提取以及保存的模式较少,获得的模式不足以概括样本的所有有效信息,得不到样本的特定规律,导致识别同样模式新样本的能力较差,学习能力较差。
当隐藏层节点个数过多时,学习时间变长,神经网络的学习能力较强,能学习较多输入数据之间的隐含模式,但是一般来说输入数据之间与输出数据相关的模式个数未知,当学习能力过强时,有可能把训练输入样本与输出数据无关的非规律性模式学习进来,而这些非规律性模式往往大部分是样本噪声,这种情况叫作过拟合(Over Fitting)。
过拟合是记住了过多和特定样本相关的信息,当新来的样本含有相关模式但是很多细节并不相同时,预测性能并不是太好,降低了泛化能力。这种情况的表现往往是在训练数据集上误差极小,在测试数据集上误差较大。
具体隐藏层神经元个数的多少取决于样本中蕴含规律的个数以及复杂程度,而样本蕴含规律的个数往往和样本数量有关系。确定网络隐藏层参数的一个办法是将隐藏层个数设置为超参,使用验证集验证,选择在验证集中误差最小的作为神经网络的隐藏层节点个数。还有就是通过简单的经验设置公式来确定隐藏层神经元个数:
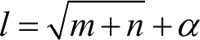
其中,l 为隐藏层节点个数,m 是输入层节点个数,n 是输出层节点个数,α 一般是 1~10 的常数。
MLP 在 20 世纪 80 年代的时候曾是相当流行的机器学习方法,拥有广泛的应用场景,譬如语音识别、图像识别、机器翻译等,但自 20 世纪 90 年代以来,MLP 遇到来自更为简单的支持向量机的强劲竞争。由于深度学习的成功,MLP 又重新得到了关注。
前馈神经网络
不同的人工神经网络有着不同网络连接的拓扑结构,比较直接的拓扑结构是前馈网络,它是最早提出的多层人工神经网络。在前馈神经网络中,每一个神经元分别属于不同的层,每一层的神经元可以接收前一层神经元的信号,并产生信号输出到下一层的神经元。第 0 层神经元叫输入层,最后一层神经元叫输出层,其他处于中间层的神经元叫隐藏层。在前馈神经网络(Feedforward Neural Network,FNN)中,每一层的神经元可以接收前一层神经元的信号,并产生信号输出到下一层。整个网络中无反馈,信号从输入层向输出层单向传播。
前馈神经网络通过下面的公式进行信息传播:
z(l)=W(l)·a(l-1)+b(l) a(l)=fl(z(l))其中:
- l:表示神经网络的层数。
- m(l):表示第 l 层神经元的个数。
- fl (·):表示第 l 层神经元的激活函数。
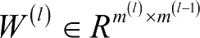
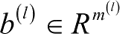
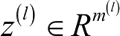
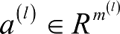
这样前馈神经网络通过逐层的信息传递,得到网络最后的输出。整个网络可以看作一个复合函数,将向量 X 作为第 1 层的输入 a(0),将第 L 层的输出 a(L) 作为整个函数的输出。
a(l)=φ(X,W,b)
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: