MATLAB gradient()函数的用法(附带实例)
MATLAB 有专门求解梯度的函数 gradient(),可对实数矩阵求梯度。
gradient() 函数的调用格式及说明如下表所示:
【实例 1】计算 xe^(-x^2-y^2) 的方向导数,绘制等值线和向量图。MATLAB 程序如下:

图 1 等高线和箭头图
【实例 2】计算 z=xe^x+sin(y^2−x^2+5)的数值梯度,并绘制等值线和向量图。MATLAB 程序如下:
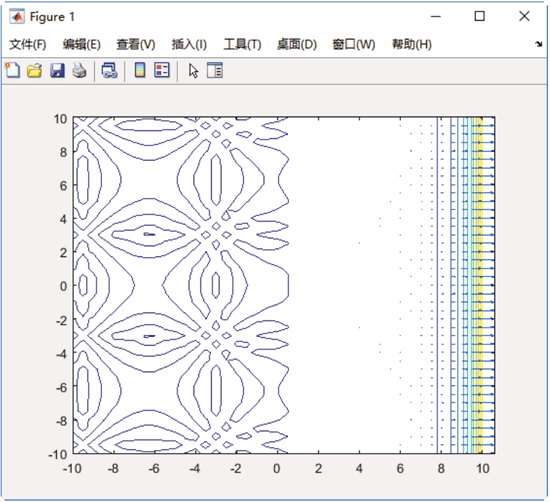
图 2 数值梯度表
gradient() 函数的调用格式及说明如下表所示:
| 调用格式 | 说明 |
|---|---|
| FX=gradient (F) | 计算对水平方向的梯度 |
| [FX,FY]=gradient (F) | 计算矩阵 F 的三维数值梯度的 x 和 y 分量,其中 Fx 为 x 方向梯度,Fy 为 y 方向梯度。点之间的间距默认为 1 |
| [FX,FY,FZ,…,FN] = gradient(F) | 计算 F 的数值梯度的 N 个分量,F 是一个 N 维数组 |
| [···]=gradient (F,h) | 使用 h 作为每个方向上的点之间的均匀间距,可以指定上述语法中的任何输出参数 |
| [···]=gradient (F,hx,hy,hz,…,hN) | 为 F 的每个维度的间距指定 N 个间距参数 |
【实例 1】计算 xe^(-x^2-y^2) 的方向导数,绘制等值线和向量图。MATLAB 程序如下:
>> close all % 关闭当前已打开的文件 >> clear % 清除工作区的变量 >> x = -2:0.2:2; % 定义介于-2~2、间隔值为0.2的线性分隔值组成的向量x >> y = x'; % 将向量x转置并赋值给y >> z = x .* exp(-x.^2 - y.^2); % 定义表达式z % 计算z的数值梯度,各个方向的间隔为1,并返回水平方向和垂直方向的梯度 >> [px,py] = gradient(z); >> figure % 创建一个图窗 >> contour(x,y,z) % 通过指定z中各值的x和y坐标,创建一个包含z的等值线的等值线图 >> hold on % 保留当前坐标区中的绘图 >> quiver(x,y,px,py) % 在x和y中每个对应元素对组所指定的坐标处绘制向量px和py的箭头图 >> hold off % 关闭图窗保持命令运行结果为:

图 1 等高线和箭头图
【实例 2】计算 z=xe^x+sin(y^2−x^2+5)的数值梯度,并绘制等值线和向量图。MATLAB 程序如下:
>> close all % 关闭当前已打开的文件 >> clear % 清除工作区的变量 >> v = -10:0.5:10; % 定义介于-10~10,间隔值为0.5的线性分隔值组成的向量v >> [x,y] = meshgrid(v); % 基于向量 v中包含的坐标返回二维网格坐标 >> z = x .*exp(x)+sin(y.^2-x.^2+5); % 定义表达式z % 指定水平方向和垂直方向的求导间距均为0.2,计算z各个位置的梯度值 >> [px,py] = gradient(z,0.2,0.2); >> contour(v,v,z), hold on, quiver(v,v,px,py), hold off % 绘制等值线和向量图最终绘制的等值线和向量图如下图所示:

图 2 数值梯度表
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: