MATLAB fmincon()函数求解约束优化问题(附带实例)
多元约束优化问题的标准形式为:
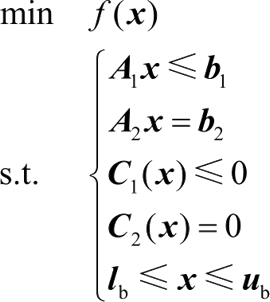
在 MATLAB 中,这种优化问题通过 fmincon() 函数求解。fmincon() 函数的调用格式如下:
1) x=fmincon(f,x0,A,b)。以 x0 为初始点,求解如下约束优化问题:
2) x=fmincon(f,x0,A,b,Aeq,beq)。以 x0 为初始点,求解如下约束优化问题:
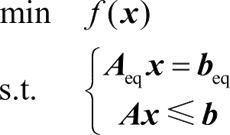
若没有不等式约束,则设Aeq=[ ],beq=[ ],此时等价于第一个调用格式。
3) x=fmincon(f,x0,A,b,Aeq,beq,lb,ub)。以 x0 为初始点,求解下面的约束优化问题:
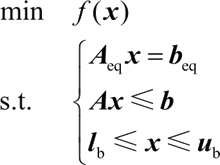
若没有界约束,则令 lb、ub 为空向量;若 x 无下界,则令 lb=-Inf;若 x 无上界,则令 ub=Inf。
4) x=fmincon(f,x0,A,b,Aeq,beq,lb,ub,nonlcon)。以 x0 为初始点,求解约束优化问题:
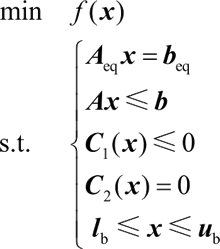
其中,nonlcon() 函数的定义如下:
5) x=fmincon(f,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)。options 为指定优化参数(见表 2),可以由 optimset 进行设置。
6) x=fmincon(problem)。返回结构体 problem 指定的问题的最小值。
7) [x,fval]=fmincon(…)。除了输出最优解 x 外,还输出相应目标函数最优值 fval。
8) [x,fval,exitflag,output]=fmincon(…)。在实现上述调用格式对应功能的基础上,输出终止迭代的条件信息 exitflag,以及关于算法的信息变量 output。exitflag 的值及含义说明如表 1 所示;output 的内容如表 2 所示。
9) [x,fval,exitflag,output,lambda,g,H]=fmincon(…)。在实现上述调用格式对应功能的基础上,输出各个约束所对应的拉格朗日乘子、目标函数在最优解 x 处的梯度 g、目标函数在最优解 x 处的黑塞(Hessian)矩阵 H。拉格朗日乘子 lambda 是一个结构体变量,其内容如下表所示。
【实例】求下面优化问题的最优解,并求出的相应梯度、黑塞(Hessian)矩阵以及拉格朗日乘子。
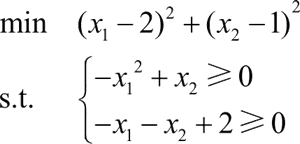
先将该优化问题转化为标准形式,即:
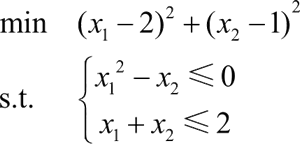
编写目标函数的 M 文件,代码如下:
编写非线性约束函数的 M 文件,代码如下:
然后在命令行窗口输入如下命令:
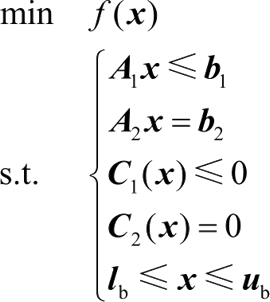
- f(x) 为目标函数,它可以是线性函数,也可以为非线性函数;
- C1(x)、C2(x)为非线性向量函数;
- A1,A2为矩阵;
- b1、b2、lb、ub为向量。
在 MATLAB 中,这种优化问题通过 fmincon() 函数求解。fmincon() 函数的调用格式如下:
1) x=fmincon(f,x0,A,b)。以 x0 为初始点,求解如下约束优化问题:
min f(x) s.t. Ax≤b
2) x=fmincon(f,x0,A,b,Aeq,beq)。以 x0 为初始点,求解如下约束优化问题:
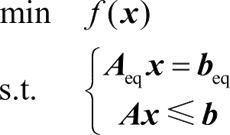
若没有不等式约束,则设Aeq=[ ],beq=[ ],此时等价于第一个调用格式。
3) x=fmincon(f,x0,A,b,Aeq,beq,lb,ub)。以 x0 为初始点,求解下面的约束优化问题:
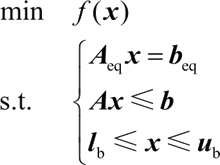
若没有界约束,则令 lb、ub 为空向量;若 x 无下界,则令 lb=-Inf;若 x 无上界,则令 ub=Inf。
4) x=fmincon(f,x0,A,b,Aeq,beq,lb,ub,nonlcon)。以 x0 为初始点,求解约束优化问题:
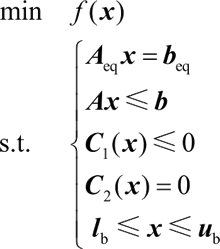
其中,nonlcon() 函数的定义如下:
function [C1,C2,GC1,GC2]=nonlcon(x)
C1=… % x处的非线性不等式约束
C2=… % x处的非线性等式约束
if nargout>2
GC1=… % 非线性不等式约束在x处的梯度
GC2=… % 非线性等式约束在x处的梯度
end
5) x=fmincon(f,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)。options 为指定优化参数(见表 2),可以由 optimset 进行设置。
6) x=fmincon(problem)。返回结构体 problem 指定的问题的最小值。
7) [x,fval]=fmincon(…)。除了输出最优解 x 外,还输出相应目标函数最优值 fval。
8) [x,fval,exitflag,output]=fmincon(…)。在实现上述调用格式对应功能的基础上,输出终止迭代的条件信息 exitflag,以及关于算法的信息变量 output。exitflag 的值及含义说明如表 1 所示;output 的内容如表 2 所示。
| exitflag 的值 | 说明 |
|---|---|
| 1 | 表示已满足一阶最优性条件 |
| 2 | 表示相邻两次迭代点的变化小于预先给定的容忍度(除 active-set 之外的所有算法) |
| 3 | 表示目标函数值在相邻两次迭代点处的变化小于预先给定的容忍度(只适用于 trust-region-reflective 算法) |
| 4 | 表示搜索方向的级小于给定的容忍度且约束的违背量小于 options.TolCon(只适用于 active-set 算法) |
| 5 | 表示方向导数的级小于给定的容忍度且约束的违背量小于 options.TolCon(只适用于 active-set 算法) |
| 0 | 表示迭代次数超过 options.MaxIter 或函数的赋值次数超过 options.FunEvals |
| -1 | 表示算法被输出函数终止 |
| -2 | 表示该优化问题没有可行解 |
| -3 | 表示目标函数在当前迭代低于 options.ObjectiveLimit,最大约束违背量小于 options.ConstraintTolerance(只适用于 interior-point,sqp-legacy 和 sqp 算法) |
| output 结构 | 说明 |
|---|---|
| iterations | 迭代次数 |
| funcCount | 函数赋值次数 |
| lssteplength | 相对于搜索方向的线性搜索步长(只适用于 active-set 和 sqp 算法) |
| stepsize | 算法在最后一步所选取的步长 |
| algorithm | 函数所调用的算法 |
| cgiterations | 共轭梯度迭代次数(只适用于大规模算法) |
| firstorderopt | 一阶最优性条件(如果用的话) |
| message | 算法终止的信息 |
9) [x,fval,exitflag,output,lambda,g,H]=fmincon(…)。在实现上述调用格式对应功能的基础上,输出各个约束所对应的拉格朗日乘子、目标函数在最优解 x 处的梯度 g、目标函数在最优解 x 处的黑塞(Hessian)矩阵 H。拉格朗日乘子 lambda 是一个结构体变量,其内容如下表所示。
| lambda 结构 | 说明 |
|---|---|
| lower | 表示下界约束 x≥lb 对应的拉格朗日乘子向量 |
| upper | 表示上界约束 x≤ub 对应的拉格朗日乘子向量 |
| ineqlin | 表示不等式约束对应的拉格朗日乘子向量 |
| eqlin | 表示等式约束对应的拉格朗日乘子向量 |
| ineqnonlin | 表示非线性不等式约束对应的拉格朗日乘子向量 |
| eqnonlin | 表示非线性等式约束对应的拉格朗日乘子向量 |
【实例】求下面优化问题的最优解,并求出的相应梯度、黑塞(Hessian)矩阵以及拉格朗日乘子。
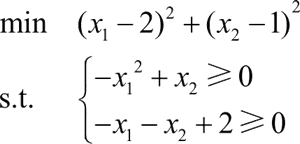
先将该优化问题转化为标准形式,即:
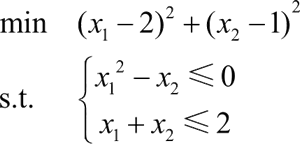
编写目标函数的 M 文件,代码如下:
function y=yhzyj(x) y=(x(1)-2)^2+(x(2)-1)^2;
编写非线性约束函数的 M 文件,代码如下:
function [c1,c2]=nonlin(x) c1=x(1)^2-x(2); c2=[]; % 没有非线性等式约束
然后在命令行窗口输入如下命令:
>> close all % 关闭当前已打开的文件
>> clear % 清除工作区的变量
>> A=[1 1]; % 输入约束条件系数矩阵
>> b=2; % 输入约束条件右端项
>> Aeq=[];beq=[];lb=[];ub=[]; % 没有非线性等式约束及界约束
>> x0=[0 0]'; % 初始点
% 以 x0 为初始点,求解约束优化问题
>> [x,fval,exitflag,output,lambda,g,H]=fmincon(@hyz,x0,A,b,Aeq,beq,lb,ub,@nonlin)
Local minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the default value of the optimality tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.
<stopping criteria details>
x = % 最优解
1.0000
1.0000
fval = % 最优值
1.0000
exitflag = % 说明解已经满足一阶最优性条件
1
output = % 包含以下字段的 struct:
iterations: 10 % 共迭代 10 次
funcCount: 33 % 函数赋值 33 次
constrviolation: 0 % 函数错误 0 次
stepsize: 1.4912e-07 % 算法最后一步所选的步长
algorithm: 'interior-point' % 所调用的算法
firstorderopt: 2.0000e-06 % 一阶最优性条件
cgiterations: 0 % 没有共轭梯度迭代
message: 'Local minimum found that satisfies the constraints.' % 说明
Optimization completed because the objective function is non-decreasing in
.feasible directions, to within the default value of the optimality tolerance,
.and constraints are satisfied to within the default value of the constraint tolerance.
.Stopping criteria details:.Optimization completed.The relative first-order optimality measure,
.9.999983e-07,.is less than options.OptimalityTolerance = 1.000000e-06, and the relative maximum constraint-violation,
.0.000000e+00,.is less than options.ConstraintTolerance = 1.000000e-06.--Optimization Metric Options:.relative first-order
.optimality = 1.0e-06 OptimalityTolerance = 1e-06 (default):.relative max(constraint violation) = 0.0e+00
.ConstraintTolerance = 1e-06 (default)
lambda = % 相应的拉格朗日乘子
包含以下字段的 struct:
eqlin: [0x1 double] % 等式约束对应的拉格朗日乘子
ineqlin: 0.6667 % 线性不等式所对应的拉格朗日乘子
lower: [2x1 double] % 下界约束对应的拉格朗日乘子
upper: [2x1 double] % 上界约束对应的拉格朗日乘子
ineqnonlin: 0.6667 % 非线性不等式约束对应的拉格朗日乘子
eqnonlin: [] % 非线性等式约束对应的拉格朗日乘子
g = % 目标函数在最优解处的梯度
-2.0000
0.0000
H = % 目标函数在最优解处的海色矩阵
3.1120 0.1296
0.1296 1.9335
 ICP备案:
ICP备案: 公安联网备案:
公安联网备案: